
2. 如图1所示,物体A、B、C叠放在水平桌面上,力F作用在物体C上后,各物体仍保持静止状态,那么以下说法正确的是 ………………………………………………………( )
如图1所示,物体A、B、C叠放在水平桌面上,力F作用在物体C上后,各物体仍保持静止状态,那么以下说法正确的是 ………………………………………………………( )
A.C不受摩擦力作用
B.B不受摩擦力作用
C.A受的各个摩擦力的合力不为零
D.A、B、C三个物体组成的整体所受摩擦力为零
1.某一物体在斜面上保持静止状态,下列说法中正确的是 ……………………………( )
A.重力可分解为沿斜面向下的分力与对斜面的压力
B.重力沿斜面向下的分力与斜面对物体的静摩擦力是平衡力
C.物体对斜面的压力与斜面对物体的支持力是平衡力
D.重力垂直于斜面方向的分力与斜面对物体的支持力是平衡力
21、解、(Ⅰ)证明:令x=y=0,∴2f(0)=f(0),∴f(0)=0 令y=-x,则f(x)+f(-x)=f(0)=0 ∴f(x)+f(-x)=0 ∴f(-x)=-f(x) ∴f(x)为奇函数
(Ⅱ)解:f(x1)=f(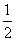 )=-1,f(xn+1)=f(
)=-1,f(xn+1)=f( )=f(
)=f(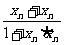 )=f(xn)+f(xn)=2f(xn)
)=f(xn)+f(xn)=2f(xn)
∴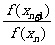 =2即{f(xn)}是以-1为首项,2为公比的等比数列 ∴f(xn)=-2n-1
=2即{f(xn)}是以-1为首项,2为公比的等比数列 ∴f(xn)=-2n-1
(Ⅲ)解:
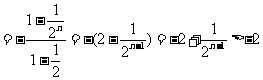 而
而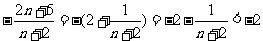 ∴
∴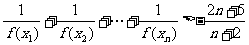
20、解:(Ⅰ)由题意: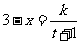 将
将
当年生产x(万件)时,年生产成本=年生产费用+固定费用=32x+3=32(3-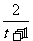 )+3,当销售x(万件)时,年销售收入=150%[32(3-
)+3,当销售x(万件)时,年销售收入=150%[32(3-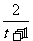 +3]+
+3]+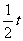 由题意,生产x万件化妆品正好销完 ∴年利润=年销售收入-年生产成本-促销费 即
由题意,生产x万件化妆品正好销完 ∴年利润=年销售收入-年生产成本-促销费 即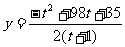 (t≥0)
(t≥0)
(Ⅱ)∵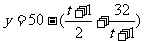 ≤50-
≤50- =42万件 当且仅当
=42万件 当且仅当 即t=7时,ymax=42 ∴当促销费定在7万元时,利润增大.
即t=7时,ymax=42 ∴当促销费定在7万元时,利润增大.
19. (1)
 (2)方程
(2)方程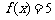 的解分别是
的解分别是 和
和 ,
,
由于 在
在 和
和 上单调递减,
上单调递减,
在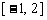 和
和 上单调递增,因此
上单调递增,因此
 .
.
由于 .
.
(3)[解法一] 当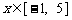 时,
时, .
. 

 ,
,
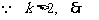
 . 又
. 又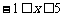 ,
,
① 当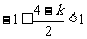 ,即
,即 时,取
时,取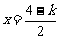 ,
,

 .
.
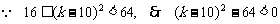 , 则
, 则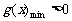 .
.
② 当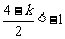 ,即
,即 时,取
时,取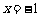 ,
,  =
=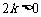 .
.
由 ①、②可知,当 时,
时, ,
,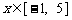 .
.
因此,在区间 上,
上, 的图像位于函数
的图像位于函数 图像的上方.
图像的上方.
[解法二] 当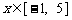 时,
时, .由
.由 得
得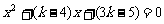 ,
,
令 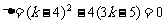 ,解得
,解得  或
或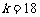 ,
,
在区间 上,当
上,当 时,
时,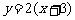 的图像与函数
的图像与函数 的图像只交于一点
的图像只交于一点 ;
;
当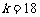 时,
时,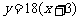 的图像与函数
的图像与函数 的图像没有交点.
的图像没有交点.
如图可知,由于直线 过点
过点 ,当
,当 时,直线
时,直线 是由直线
是由直线
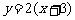 绕点
绕点 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间 上,
上, 的图像
的图像
位于函数 图像的上方.
图像的上方.
18.解:⑴由题意, ,
,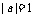 又
又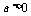 ,所以
,所以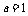 。
。
⑵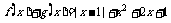
当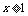 时,
时,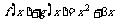 ,它在
,它在 上单调递增;
上单调递增;
当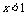 时,
时, ,它在
,它在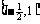 上单调递增。
上单调递增。
.
17.解: (1)由已知对任意的 、
、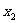
 ,且
,且 ,都有
,都有 ,
,
从而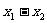 与
与 异号,所以
异号,所以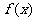 在[-1,1]上是减函数
在[-1,1]上是减函数
(2)因为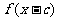 的定义域是
的定义域是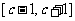 ,
, 的定义域是
的定义域是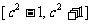 , 因为以上两个集合的交集为空集,所以
, 因为以上两个集合的交集为空集,所以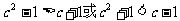 解得:
解得: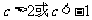
16、解:
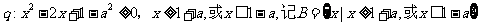
而
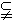
 ,即
,即 。
。
9、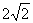 ;
10、
;
10、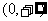 ; 11、; 12、偶函数; 13.
; 11、; 12、偶函数; 13. 14.
14.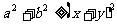 15.2
15.2
8、C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com