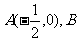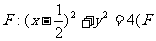6． (2005重庆)已知是圆为圆心)上一动点，线段AB的垂直平分线交BF于P，则动点P的轨迹方程为　　　　　　　　 ．

简答提示：1．C；2．D；3． ；

5．已知P是椭圆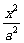+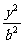＝1(a＞b＞0)上任意一点，P与两焦点连线互相垂直，且P到两准线距离分别为6、12，则椭圆方程为____________．

4．已知F₁为椭圆的左焦点，A、B分别为椭圆的右顶点和上顶点，P为椭圆上的点，当PF₁⊥F₁A，PO∥AB(O为椭圆中心)时，则椭圆的离心率为________．

3．点P在椭圆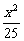+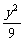=1上，它到左焦点的距离是它到右焦点距离的两倍，则点P的横坐标是____________．

2．(2005全国卷Ⅲ)设椭圆的两个焦点分别为F_1、、F₂，过F₂作椭圆长轴的垂线交椭圆于点P，若△F₁PF₂为等腰直角三角形，则椭圆的离心率是　　　　　　　　　　　　　　　　 (　 )

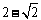A．　　　　　　 B．　　　　 C．　 　　　　　 D．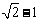

[填空题]

1．(2004全国I)椭圆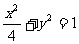的两个焦点为F₁、F₂，过F₁作垂直于x轴的直线与椭圆相交，一个交点　 为P，则=　　　 (　　 )

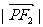A．　　　　　　　　　 B．　　　　　　　　　　 C．　　　　　　　　　　　 D．4

4．会用方程分析解决交点、弦长和求值问题，能正确使用“点差法”及其结论。

同步练习　　　　　 8．1 椭圆方程及性质 　

[选择题]

3．要正确理解和灵活运用参数a,b,c,,e的几何意义与相互关系；

2．求椭圆方程，常用待定系数法,定义法,首先确定曲线类型和方程的形式，再由题设条件确定参数值，应“特别”掌握；

(1)当焦点位置不确定时，方程可能有两种形式，应防止遗漏；

(2)两种标准方程中，总有a＞b＞0，c²=a²-b²并且椭圆的焦点总在长轴上；

1．椭圆定义是解决问题的出发点,一般地，涉及a、b、c的问题先考虑第一定义，涉及e、d及焦半径的问题行急需处理 虑第二定义；