
3. 下列各句中,没有语病的一句是
A.近几年来,世界各地频繁出现沙尘暴、酸雨等气候异常现象,其影响范围、持续时间和危害程度比过去都严重得多。
B.青年的思想道德状况,青年的科学文化素质,青年的人文精神和创新能力,将成为衡量我们的社会是否和谐的重要标志。
C.古老的智慧、经典的知识尽管难以具有实际的功效,但它具有益人心智、怡人性情、改变气质、滋养人生的价值不可小视。
D.现在越来越多的商家利用节日大打价格战,在商场里,减价的标牌随处可见,三折、四折甚至五折,非常诱人。
2. 下列加点成语使用正确的一项是
A.盛夏的深夜,学生们都沉睡在香甜的美梦中了,这个临近大河的校园里却蛙声阵阵,沸反盈天。
B.与13亿人的利益息息相关的《物权法》,历时五年,经过八次审议,从分歧严重的争论到达成共识,3月16日终于在十届全国人大五次会议上获得表决通过。
C.备受关注的手机单项收费问题正由有关部门进行可行性论证,一项有利于手机使用者的政策即将呼之欲出。
D.冯小刚的贺岁片《天下无贼》在泰州上映时,票房率大增,中途退场的观众可以说是凤毛麟角。
1.下列词语中加点的字,每对的读音都不相同的一组是( )
A.卡片/关卡 宿仇/星宿 蹊跷/另辟蹊径 差可告慰/差强人意
B.落笔/落枕 刹那/古刹 伺候/伺机报复 犯而不校/校本课程
C.似的/相似 提防/提醒 模范/大模大样 层见叠出/瑕瑜互见
D.称谓/相称 哽咽/吞咽 铜臭/乳臭未干 擢发难数/数见不鲜
10.(2005上海) 如图,点A、B分别是椭圆 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于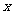 轴上方,
轴上方, .
.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于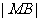 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离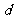 的最小值.
的最小值.

解:(1)由已知可得点A(-6,0),F(4,0)
设点P的坐标是 ,由已知得
,由已知得
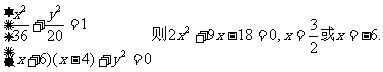
则2x2+9x-18=0,
 , ∴P点的坐标是
, ∴P点的坐标是
(2)直线AP的方程是
设点M的坐标是(m,0),则M到直线AP的距离是 ,
,
于是
椭圆上的点 到点M的距离d有
到点M的距离d有

由于
[探索题](2006湖北)设A、B分别为椭圆 (
(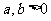 )的左、右顶点,椭圆长半轴的长等于焦距,且
)的左、右顶点,椭圆长半轴的长等于焦距,且 为它的右准线。
为它的右准线。
(Ⅰ)求椭圆的方程;
(Ⅱ)设P为右准线上不同于点(4,0)的任意一点,若直线AP、BP分别与椭圆相交于异于A、B的点M、N,证明点B在以MN为直径的圆内。
解(Ⅰ)依题意得 解得
解得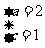 从而
从而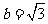
故椭圆方程为
(Ⅱ)解法1:由(Ⅰ)得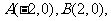 设
设
 M点在椭圆上,
M点在椭圆上, ①
又M点异于顶点A、B,
①
又M点异于顶点A、B,
由P、A、M三点共线可得 从而
从而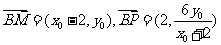
∴ ②
②
将①式代入②式化简得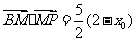
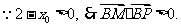 于是
于是 为锐角,从而
为锐角,从而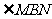 为钝角,
为钝角,
故点B在以MN为直径的圆内。
解法二:由(Ⅰ)得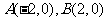 .设
.设 ,
,
则直线AP的方程为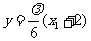 ,直线BP的方程为
,直线BP的方程为 .
.
 点M、N分别在直线AP、BP上,
点M、N分别在直线AP、BP上,
 .从而
.从而 ③
③
联立 消去
消去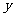 得
得 =0
=0
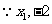 是方程的两根,
是方程的两根, ,即
,即 ④
④
又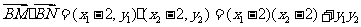 ⑤
⑤
于是由③、④式代入⑤式化简可得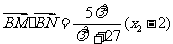
 N点在椭圆上,且异于顶点A、B,
N点在椭圆上,且异于顶点A、B, 又
又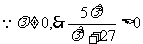 ,
,
从而
故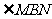 为钝角,即点B在以MN为直径的圆内。
为钝角,即点B在以MN为直径的圆内。
解法3:由(Ⅰ)得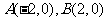 ,设
,设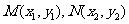
则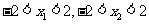 .又MN的中点Q的坐标为
.又MN的中点Q的坐标为 ,
,
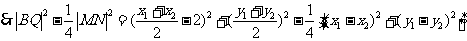
化简得 ⑥
⑥
直线AP的方程为 ,直线BP的方程为
,直线BP的方程为
 点P在准线
点P在准线 上,
上,
 ,即
,即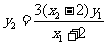 ⑦
⑦
又M点在椭圆上, ,即
,即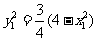 ⑧
⑧
于是将⑦、⑧式代入⑥式化简可得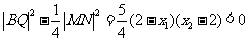
从而B在以MN为直径的圆内。
9. 如下图,已知△OFQ的面积为S,且 ·
· =1.
=1.

(1)若 <S<2,求向量
<S<2,求向量 与
与 的夹角θ的取值范围;
的夹角θ的取值范围;
(2)设| |=c(c≥2),S=
|=c(c≥2),S=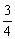 c,若以O为中心,F为一个焦点的椭圆经过点Q,当|
c,若以O为中心,F为一个焦点的椭圆经过点Q,当| |取最小值时,求椭圆的方程.
|取最小值时,求椭圆的方程.
解:(1)由已知,得

 |
| ||
|| |sin(π-θ)=S,
|sin(π-θ)=S,
| ||
|| |cosθ=1.
|cosθ=1.
∴tanθ=2S.
∵ <S<2,∴1<tanθ<4.
<S<2,∴1<tanθ<4.
则 <θ<arctan4.
<θ<arctan4.
(2)以O为原点, 所在直线为x轴建立平面直角坐标系.
所在直线为x轴建立平面直角坐标系.
设椭圆方程为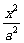 +
+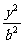 =1(a>b>0),Q(x,y).
=1(a>b>0),Q(x,y).
 =(c,0),则
=(c,0),则 =(x-c,y).
=(x-c,y).
∵ |
| |·y=
|·y=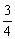 c,∴y=
c,∴y= .
.
又∵ ·
· =c(x-c)=1,∴x=c+
=c(x-c)=1,∴x=c+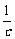 .
.
则| |=
|= =
= (c≥2).
(c≥2).
可以证明:当c≥2时,函数t=c+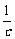 为增函数,
为增函数,
∴当c=2时,
| |min=
|min= =
=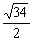 ,
,
此时Q( ,
, ).将Q的坐标代入椭圆方程,
).将Q的坐标代入椭圆方程,
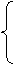
|
|
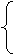
 +
+ =1, a2=10,
=1, a2=10,
a2-b2=4. b2=6.
∴椭圆方程为 +
+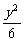 =1.
=1.
8. 如下图,设E: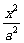 +
+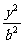 =1(a>b>0)的焦点为F1与F2,且P∈E,∠F1PF2=2θ.
=1(a>b>0)的焦点为F1与F2,且P∈E,∠F1PF2=2θ.
求证:△PF1F2的面积S=b2tanθ.
剖析:有些圆锥曲线问题用定义去解决比较方便.如本题,设|PF1|=r1,|PF2|=r2,则S= r1r2sin2θ.若能消去r1r2,问题即获解决.
r1r2sin2θ.若能消去r1r2,问题即获解决.

证明:设|PF1|=r1,|PF2|=r2,
则S= r1r2sin2θ,又|F1F2|=2c,
r1r2sin2θ,又|F1F2|=2c,
由余弦定理有
(2c)2=r12+r22-2r1r2cos2θ=(r1+r2)2-2r1r2-2r1r2cos2θ=(2a)2-2r1r2(1+cos2θ),
于是2r1r2(1+cos2θ)=4a2-4c2=4b2.
所以r1r2= .
.
这样即有S= ·
· sin2θ=b2
sin2θ=b2 =b2tanθ.
=b2tanθ.
评述:解与△PF1F2(P为椭圆上的点)有关的问题,常用正弦定理或余弦定理,并结合|PF1|+|PF2|=2a来解决.
7. 已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1与椭圆相交于点P和点Q,且OP⊥OQ,|PQ|= ,求椭圆方程.
,求椭圆方程.
解:设椭圆方程为mx2+ny2=1(m>0,n>0),
设P(x1,y1),Q(x2,y2),解方程组
 y=x+1,
y=x+1,
mx2+ny2=1.
消去y,整理得(m+n)x2+2nx+n-1=0.
Δ=4n2-4(m+n)(n-1)>0,即m+n-mn>0,OP⊥OQ x1x2+y1y2=0,
x1x2+y1y2=0,
即x1x2+(x1+1)(x2+1)=0,2x1x2+(x1+x2)+1=0,∴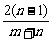 -
-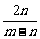 +1=0.
+1=0.
∴m+n=2. ①
由弦长公式得2· =(
=( )2,将m+n=2代入,得m·n=
)2,将m+n=2代入,得m·n=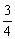 . ②
. ②

|
|
 m=
m= , m=
, m= ,
,
n= n=
n= .
.
∴椭圆方程为 +
+ y2=1或
y2=1或 x2+
x2+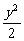 =1.
=1.
5. 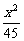 +
+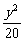 =1; 6.
=1; 6. 
[解答题]
4. ∵|PF1|= , AB∥PO,ΔOPF1∽ΔABO
, AB∥PO,ΔOPF1∽ΔABO
∴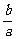 =
= . b=c. ∴e=
. b=c. ∴e=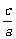 =
= =
=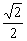 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com