2．已知|a|＝2，|b|＝4，向量a与b的夹角为60°，当(a+3b)⊥(ka－b)时，实数k的值是(　)

A.　 　　　　　 B.　 　　 C.　 　 D.

解析：依题意得a·b＝|a|·|b|·cos 60°＝2×4×＝4，因为(a+3b)⊥(ka－b)，所以(a+3b)·(ka－b)＝0，得ka²+(3k－1)a·b－3b²＝0，即k+3k－1－12＝0，解得k＝.

答案：C

1．(2009·辽宁)平面向量a与b的夹角为60°，a＝(2,0)，|b|＝1，则|a+2b|＝(　)　　　　　　　　　　　　　　　　　

A.　 B．2　 C．4　 D．12

解析：因为a＝(2,0)，|b|＝1，所以|a|＝2，a·b＝2×1×cos 60°＝1，故|a+2b|＝＝2.

答案：B

1．设a＝(sin x，)，b＝，且a∥b，则锐角x为(　)

A.　 　　 B.　 　　 C.　 　　 　D.π

解析：∵a＝，b＝，且a∥b，∴sin xcos x－×＝0，

即sin 2x－＝0，∴sin 2x＝1.又∵x为锐角，∴2x＝，x＝.

答案：B

10．(2010·浙江金华调研)已知点A(1,0)、B(0,2)、C(－1，－2)，求以A、B、C为顶点的平行四边形的第四个顶点D的坐标．

解答：(1)设D点坐标为(x，y)，

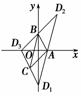
若是▱ABCD，则由AB＝DC得(－1,2)＝(－1－x，－2－y)，

∴∴x＝0，y＝－4.∴D点的坐标为(0，－4)(如图中的D₁)．

(2)若是▱ADBC，则由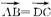得(x－1，y)＝(1,4)．

解得x＝2，y＝4.∴D点坐标为(2,4)(如图中的D₂)．

(3)若是▱ABDC，则由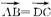得(－1,2)＝(x+1，y+2)．解得x＝－2，y＝0.

∴D点的坐标为(－2,0)(如图中的D₃)．

综上所述，以A、B、C为顶点的平行四边形的第四个顶点D的坐标为(0，－4)或(2,4)或(－2,0)．

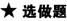
9．已知点O(0,0)，A(1,2)，B(4,5)，且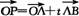 (t∈R)，问：

(1)t为何值时，点P在x轴上？点P在第二、四象限角平分线上？点P在第二象限？

(2)四边形OABP能否成为平行四边形？若能，求出相应的t值；若不能，请说明理由．

解答：(1)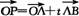＝(1+3t,2+3t)．若P在x轴上，只需2+3t＝0，t＝－；

若P在第二、四象限角平分线上，则1+3t＝－(2+3t)，t＝－；

若P在第二象限，则需，－<t<－.

(2) 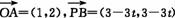＝(3－3t,3－3t)．若OABP为平行四边形，则.

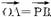，无解．

四边形OABP不能成为平行四边形．

8．向量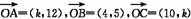＝(10，k)，当k为何值时，A、B、C三点共线？

解答：解法一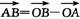：∵＝(4,5)－(k,12)＝(4－k，－7)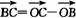，＝(10，k)－(4,5)＝(6，k－5)．∵A、B、C三点共线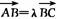，∴，即(4－k，－7)＝λ(6，k－5)＝(6λ，(k－5)λ)．

∴解得k＝11或－2.

解法二：接解法一，∵A、B、C三点共线，∴(4－k)(k－5)＝6×(－7)，解得k＝11

或－2.

7．已知向量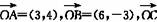＝(5－m，－3－m)，若点A、B、C能构成三角形，则实数m应满足的条件是________．

解析：因为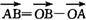＝(3，－7)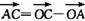，＝(2－m，－7－m)，又点A、B、C

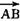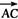能构成三角形．所以点A、B、C不共线，即与不共线．所以3×(－7－

m)－(－7)×(2－m)≠0，解得m≠－，故实数m应满足m≠－.

答案：m≠－

6．(2009·辽宁)在平面直角坐标系xOy中，四边形ABCD的边AB∥DC，AD∥BC.已知点A(－2,0)，B(6,8)，C(8,6)，则D点的坐标为________．

解析：设D(x，y)，因为AB∥DC，AD∥BC，所以,

而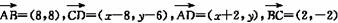，所以

解之得x＝0，y＝－2，故D(0，－2)．

答案：(0，－2)

5．已知平面向量a＝(1,2)，b＝(－2，m)，且a∥b，则2a+3b＝________.

解析：由a＝(1,2)，b＝(－2，m)，且a∥b，得1×m＝2×(－2)⇒m＝－4，从而a＝(1,2)，b＝(－2，－4)，那么2a+3b＝2(1,2)+3(－2，－4)＝(－4，－8)．

答案：(－4，－8)

2．(★★★★)如右图所示，设P、Q为△ABC内的两点，且＝+，＝+，则△ABP的面积与△ABQ的面积之比为________．

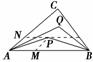
解析：如图所示，设＝，＝，则＝+，由向量的平行四边形法则，知NP∥AB，所以＝＝，

同理可得＝，故＝.