2．下列命题正确的是(　)

A．若ac＞bc⇒a＞b　 　　　　　　　　 B． 若a²＞b²⇒a＞b

C．若＞⇒a＜b　 　　　　　　　 D．若＜⇒a＜b

解析：对于A，若c＜0，其不成立；对于B，若a、b均小于0或a＜0，其不成立；对于C，若a＞0，b＜0，其不成立；对于D，其中a≥0，b＞0，平方后显然有a＜b.

答案：D

1．若a>b>0，则下列不等式中一定成立的是(　)

A．a+>b+　 　　　　 B.>

C．a－>b－　 　　　　 D.>

解析：∵a>b>0，∴>，∴a+>b+.

答案：A

5．在△ABC中，sin A+cos A＝，则＝________.

解析：由已知2sin Acos A＝－，∴cos A＜0，即A为钝角，∴(sin A－cos A)²＝，

∴sin A－cos A＝，则sin A＝，cos A＝－.原式＝.

4．若钝角三角形三内角成等差数列，且最大边长与最小边长的比值为m，则m的范围是(　)

A．(1,2)　 　　　　 B．(2，+∞)　 　 C．[3，+∞)　 　 D．(3，+∞)

解析：设△ABC三内角为A、B、C，其对边为a、b、c，且A<B<C，由2∠B＝∠A+∠C，且∠A+∠B+∠C＝180°，可得∠B＝60°，由已知∠A<30°.m＝＝＝＝cot A+>2.

答案：B

3．在△ABC中，设命题p：＝＝，命题q：△ABC是等边三角形，那么命题p是命题q的(　)

A．充分不必要条件　 　　　 B．必要不充分条件

C．充要条件　 　　　　　　　 D．既不充分也不必要条件

解析：若△ABC是等边三角形，则＝＝；若＝＝，

又＝＝，则即a＝b＝c.∴p是q的充要条件．

答案：C

2．在△ABC中，已知∠B＝45°，c＝2，b＝，则∠A等于(　)

A．15°　 　　　　　 B．75°　 　　 C．105°　 　 D．75°或15°

解析：根据正弦定理＝ ，sin C＝＝＝.

∴C＝60°或C＝120°，因此A＝75°或A＝15°.

答案：D

1．在△ABC中，若∠A＝60°，b＝1，S_△ABC＝，则的值为(　)

A.　 　　　　　 B.　 　　 C.　 　　　　　 D.

解析：∵S_△ABC＝，即bcsin A＝，∴c＝4.由余弦定理a²＝b²+c²－2bccos A＝13，∴a＝，

∴＝＝＝.

答案：B

5．若cos(α+β)＝，cos(α－β)＝，则tan α·tan β＝________.

解析：∵cos(α+β)＝cos αcos β－sin αsin β＝①

cos(α－β)＝cos αcos β+sin αsin β＝②

由①②解得cos αcos β＝，sin αsin β＝，则tan αtan β＝＝.

4．sin 163°sin 223°+sin 253°sin 313°等于(　)

A．－　 　　　　　 B.　 　C．－　 　D.

解析：原式＝sin 163°·sin 223°+cos 163°cos 223°＝cos(163°－223°)＝cos(－60°)＝.

答案：B

3．等式|sin αcos α|+|sin²α－cos²α|＝成立的充要条件是(　)

A．α＝kπ(k∈Z)　 　　　　　　　　 B．α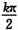＝(k∈Z)

C．α＝(k∈Z)　 　　　　　　　　 D．α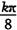＝(k∈Z)

解析：由题意知：原式＝|sin 2α|+|cos 2α|＝

∴|sin 2α|+|cos 2α|＝1，∴1+2|sin 2αcos 2α|＝1，|sin 4α|＝0，α＝(k∈Z)．

答案：C