1．若|a|＜1，|b|＜1，则|a+b|+|a－b|与2的大小关系是________．

解析：若(a+b)(a－b)≥0，则|a+b|+|a－b|＝|(a+b)+(a－b)|＝2|a|＜2；

若(a+b)(a－b)＜0，则|a+b|+|a－b|＝|(a+b)－(a－b)|＝2|b|＜2.∴|a+b|+|a－b|＜2.

答案：|a+b|+|a－b|＜2

10．设m等于|a|、|b|和1中最大的一个，当|x|＞m时，求证：|+|＜2.

证明：∵|x|＞m≥|a|，又|x|＞m≥|b|，且|x|＞m≥1，则|x|²＞|b|.

∴|+|≤||+||＝+＜+＝2，

故原不等式成立．

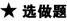
9．关于实数x的不等式|x－|≤与x²－3(a+1)x+2(3a+1)≤0(其中a∈R)的解集依次记为A与B，求使A⊆B的a的取值范围．

解答：简化集合A和B，然后对字母参数a进行讨论．

A＝{x|2a≤x≤a²+1}，B＝{x|(x－2)[x－(3a+1)]≤0}．

当3a+1≥2，即a≥时，得B＝{x|2≤x≤3a+1}．

欲使A⊆B，只要得1≤a≤3；

当3a+1＜2，即a＜时，得B＝{x|3a+1≤x≤2}．

欲使A⊆B，只要得a＝－1.

综上，使A⊆B的a的取值范围是1≤a≤3或a＝－1.

8．设f(x)＝x²－x+b，|x－a|＜1，求证：|f(x)－f(a)|＜2(|a|+1)．

证明：∵f(x)－f(a)＝(x－a)(x+a－1)，又|x－a|＜1，∴|f(x)－f(a)|＝|x－a||x+a－1|≤|x+a－1|＝|x－a+2a－1|≤|x－a|+2|a|+1＜2|a|+2＝2(|a|+1)．

7．已知a∈R，若关于x的方程x²+x+|a－|+|a|＝0有实根，则a的取值范围是________．

解析：方程即|a－|+|a|＝－x²－x，利用绝对值的几何意义(或零点分段法进行求解)可得实数a的取值范围为[0，]．

答案：[0，]

6．不等式x²＞2^－|x|的解集是________．

解析：2－x²＞2^－|x|，所以－x²＞－|x|，所以x²－|x|＜0.所以|x|(|x|－1)＜0，所以－1＜x＜0或0＜x＜1.

答案：{x|－1＜x＜0或0＜x＜1}

5．若关于x的不等式|x+3|+|x－1|＞a恒成立，则a的取值范围是________．

解析：从几何角度看不等式左侧表示数轴上的点到－3和1的距离之和，最小值为4.

答案：a＜4

4．不等式组的解集是(　)

A．{x|0＜x＜2}　 　　　　　　　　　　　 B．{x|0＜x＜2.5}

C．{x|0＜x＜}　 　　　　　　　 D．{x|0＜x＜3}

解析：解法一：由x＞0及＞0，知0＜x＜3.对＞||两边平方，整理，得x(x²－6)＜0.

从而0＜x＜，选C项．

解法二：(1)当0＜x≤2时，不等式化为(2+x)(3－x)＞(2－x)(3+x)，即2x＞0，∴0＜x≤2；

(2)当x＞2时，不等式化为(2+x)(3－x)＞(x－2)(3+x)，即x²＜6，∴2＜x＜，从而

0＜x＜.

答案：C

3．设a、b、c是互不相等的正数，则下列不等式中不恒成立的是(　)

A．|a－b|≤|a－c|+|b－c|　 　　　　 B．a²+≥a+

C．|a－b|+≥2　 　　　　　　 D.－≤－

解析：解法一：当a－b＝－1时，|a－b|+＝0，故不等式|a－b|+≥2不一定成立．

解法二：|a－b|＝|(a－c)－(b－c)|≤|a－c|+|b－c|；

a²+≥a+⇔(a+)²－(a+)－2≥0⇔(a+－2)·(a++1)≥0.

由a＞0，显然a+≥2，所以不等式成立；－≤－⇔≤，则不等式显然成立．

答案：C

2．设a∈(0,1)，则关于x的不等式|x－log_ax|＜|x|+|log_ax|的解集为(　)

A．(0，a)　 　　　　　　 B．(0,1)

C．(0，+∞)　 　　　　 D．(－∞，0)∪(1，+∞)

解析：根据绝对值不等式性质．xlog_ax＞0⇔即0＜x＜1(0＜a＜1)．

答案：B