10．圆台的一个底面周长是另一个底面周长的3倍，轴截面的面积等于392 cm²，母线与轴的夹角是45°，求这个圆台的高、母线长和两底面半径．

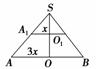
解答：圆台的轴截面如上图所示，设圆台上下底面半径分别为x cm,3x cm.延长AA₁交OO₁的延长线于S，

在Rt△SOA中，∠ASO＝45°，则∠SAO＝45°，

∴SO＝AO＝3x，∴OO₁＝2x，

又S_轴截面＝(6x+2x)·2x＝392，∴x＝7.

故圆台的高OO₁＝14 cm，母线长l＝O₁O＝14 cm，两底面半径分别为7 cm,21 cm.

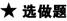
9．正四棱锥的高为，侧棱长为，求侧面上斜高(棱锥侧面三角形的高)为多少？

解答：如下图所示，正棱锥S-ABCD中高OS＝，

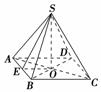
侧棱SA＝SB＝SC＝SD＝，

在Rt△SOA中，OA＝＝2，∴AC＝4.

∴AB＝BC＝CD＝DA＝2.

作OE⊥AB于E，则E为AB中点．连接SE，则SE即为斜高，则SO⊥OE.

在Rt△SOE中，

∵OE＝BC＝，SO＝，∴SE＝，即侧面上的斜高为.

8．正四棱台AC₁的高是17 cm，两底面的边长分别是4 cm和16 cm，求这个棱台的侧棱长和斜高．

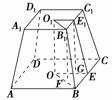
解答：如上图所示，设棱台的两底面的中心分别是O₁、O，B₁C₁和BC的中点分别是E₁和E，连接O₁O、E₁E、O₁B₁、OB、O₁E₁、OE，则四边形OBB₁O₁和OEE₁O₁都是直角梯形．

∵A₁B₁＝4 cm，AB＝16 cm，∴O₁E₁＝2 cm，OE＝8 cm，

O₁B₁＝2 cm，OB＝8 cm，

∴B₁B²＝O₁O²+(OB－O₁B₁)²＝361 cm²，E₁E²＝O₁O²+(OE－O₁E₁)²＝325 cm²，

∴B₁B＝19 cm，E₁E＝5 cm.

答：这个棱台的侧棱长为19 cm，斜高为5 cm.

7．用小正方体搭成一个几何体，右图是它的正(主)视图和侧(左)视图，搭成这个几何体的小正方体最多为________个．

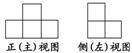
解析：画出其几何体图形，可知最多需要7个小正方体．

答案：7

6．一个几何体的三视图如图所示，则该几何体的体积等于________．

解析：三视图对应的几何体是一个棱长为2的正方体上面摆放了一个直径为2的球，因此此几何体的体积为V＝V_球+V_正方体＝π+8

答案：8+

5．有一个正三棱柱的三视图如图所示(俯视图为正三角形)，则这个三棱柱的高和底面边长分别为________．

解析：由三视图中的数据知高为2，底面边长为2×＝4.

答案：2　4

4．下列物体中的正视图和俯视图(如图)中有错误的一项是(　)

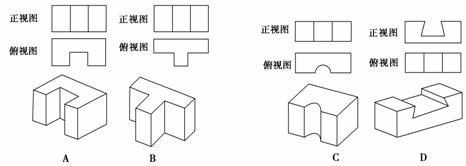
解析：将看不见的部分用虚线标出．

答案：D

3．已知一个几何体的三视图及其尺寸如图所示，正视图和侧视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，它们可能是如下各种几何图形的4个顶点，这些几何图形是(　)

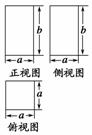
①矩形　②不是矩形的平行四边形　③有三个面为直角三角形，有一个面为等腰三角形的四面体　④每个面都是等腰三角形的四面体　⑤每个面都是直角三角形的四面体

A．①③④⑤　　　B．②③④⑤　　　C．④⑤　　　D．③④⑤

解析：由三视图知该几何体是底面为正方形的长方体．由下图可知， ①可能，②不可能，③④⑤都有可能．

答案：A

A．①②　 　　 B．①③　 　 C．①④　 　 D．②④

解析：正方体的三视图都是正方形，不合题意；圆锥的主视图和左视图都是等腰三角形，俯视图是圆，符合题意；三棱台的主视图和左视图、俯视图各不相同，不合题意；正四棱锥的主视图和左视图都是三角形，而俯视图是正方形，符合题意，所以②④正确．

答案：D

2．利用斜二测画法可以得到：①三角形的直观图是三角形；②平行四边形的直观图是平行四边形；③正方形的直观图是正方形；④菱形的直观图是菱形，以上结论正确的是(　)

A．①②　 　　 B．①　 　C．③④　 　　　　　 D．①②③④

解析：因为斜二测画法规则依据的是平行投影的性质，则①②正确；对于③④，只有平行于x轴的线段长度不变，所以不正确．

答案：A

2．已知二次函数f(x)满足|f(1)|≤1，|f(0)|≤1，|f(－1)|≤1，求证：|x|≤1时，有|f(x)|≤.

证明：设f(x)＝ax²+bx+c(a≠0)，由题意，得，

∴a＝[f(1)+f(－1)－2f(0)]，b＝[f(1)－f(1)]，c＝f(0)．

代入f(x)的表达式变形得：f(x)＝f(1)(x²+x)/2+f(－1)(x²－x)/2+(1－x²)f(0)．

∵|f(1)|≤1，|f(0)|≤1，|f(－1)|≤1，∴ 当|x|≤1时，|f(x)|≤|(x²+x)/2||f(1)|+|(x²－x)/2||f(－1)|+(1－x²)|f(0)|≤|x|(1+x)/2+|x|(1－x)/2+(1－x²)＝－x²+|x|+1

＝－(|x|－1/2)²+5/4≤5/4.