7．下列命题中正确的命题是________．

①直线l上有两点到平面α距离相等，则l∥α；

②平面α内不在同一直线上三点到平面β的距离相等，则α∥β；

③垂直于同一直线的两个平面平行；

④平行于同一直线的两平面平行；

⑤若a、b为异面直线，a⊂α，b∥α，b⊂β，a∥β，则α∥β.

答案：③⑤

6．到空间不共面的四点距离相等的平面个数为________．

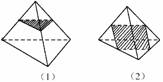
解析：如右图分类，一类如图(1)将四点视为三棱锥四个顶点，取棱中点，可以做如图(1)平面平行于三棱锥的底面，并到另一顶点距离与底面距离相等，这样的平面有4个；另一类如图(2)取各段中点，四个中点形成平面平行于三棱锥相对棱，这样的平面有3个，共7个．

答案：7

5．设α、β、γ为两两不重合的平面，l、m、n为两两不重合的直线，给出下列四个命题，其中真命题的个数是(　)

①若α⊥γ，β⊥γ，则α∥β；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；③若α∥β，l⊂α，则l∥β；④若α∩β＝l，β∩γ＝m，γ∩α＝n，l∥γ，则m∥n.

A．1　 　　　B．2 　　　　C．3　 　　　　D．4

答案：B

4．(2009·南京质检)已知平面α∥平面β，P是α、β外一点，过点P的直线m与α、β分别交于A、C，过点P的直线n与α、β分别交于B、D且PA＝6，AC＝9，PD＝8，则BD的　 长为(　)

A．16　 　　　B．24或　 　C．14　 　　D．20

解析：根据题意可出现以下如图两种情况

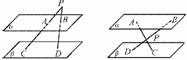
可求出BD的长分别为或24.

答案：B

3．设a、b是异面直线，下列命题正确的是(　)

A．过不在a、b上的一点P一定可以作一条直线和a、b都相交

B．过不在a、b上的一点P一定可以作一个平面和a、b都垂直

C．过a一定可以作一个平面与b垂直

D．过a一定可以作一个平面与b平行

解析：可证明过a一定有一个平面与b平行．

答案：D

2．给出下列命题，其中正确的两个命题是(　)

①直线上有两点到平面的距离相等，则此直线与平面平行；②夹在两个平行平面间的两条异面线段的中点连线平行于这两个平面；③直线m⊥平面α，直线n⊥m，则n∥α；④a、b是异面直线，则存在唯一的平面α，使它与a、b都平行且与a、b距离相等．

A．①与②　 　　B．②与③ 　　C．③与④　 　D．②与④

解析：直线上有两点到平面的距离相等，直线可能和平面相交；直线m⊥平面α，直线m⊥直线n，直线n可能在平面α内，因此①③为假命题．

答案：D

1．如图所示，在三棱柱ABC-A′B′C′中，点E、F、H、K分别为AC′、CB′、A′B、B′C′的中点，G为△ABC的重心，从K、H、G、B′中取一点作为P，使得该棱柱恰有2条棱与平面PEF平行，则P为(　)

A．K　 　　　　　　　 　　　B．H

C．G　 　　　　　　　 　　　D．B′

答案：C

5．如图，PA⊥平面ABC，∠ACB＝90°，且PA＝AC＝BC＝a，则异面直线PB与AC所成角的正切值等于________．

4．

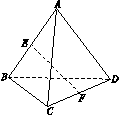
如图，已知E、F分别为正四面体ABCD所在棱的中点，则异面直线AC与EF所成的角为(　)

A．30°　 　　　　　 B．45°

C．60°　 　　　　　 D．90°

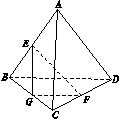
解析：如图，取BC中点G，连结EG，FG，则∠GEF为异面直线AC与EF所成角，∵EG=AC=BD=GF，又可证AC⊥BD，∴∠EGF=90°，则∠GEF=45°.

答案：B

3．ABCD为空间四边形，AB＝CD，AD＝BC，AB≠AD，M、N分别是对角线AC与BD的中点，则MN与(　)

A．AC、BD之一垂直　 　　　　 B．AC、BD都垂直

C．AC、BD都不垂直　 　　　　 D．AC、BD不一定垂直

解析：∵AD＝BC，AB＝CD，BD＝BD，∴△ABD≌△CDB.则AN＝CN，在等腰△ANC中，由M为AC的中点知MN⊥AC.同理可证MN⊥BD.

答案：B