4．矩形ABCD中，AB＝4，BC＝3，沿AC将矩形ABCD折成一个直二面角B－AC－D，则四面体ABCD的外接球的体积为(　)

A.π　 　　　　　　 B.π　 　　　　　　　　 C.π　 　　　　　 D.π

答案： C

3．二面角α－AB－β的平面角是锐角，C∈α，CD⊥β，垂足为D，E∈AB，且∠CEB是锐角，则∠CEB与∠DEB的大小关系为(　)

A．∠CEB＞∠DEB　 　　　 B．∠CEB＜∠DEB

C．∠CEB≤∠DEB　 　　　 D．∠CEB与∠DEB的大小关系不确定

解析：如下图：作DF⊥AB垂足为F，连结CF由三垂线定理知∠CFD为二面角的平面角，可知∠CED，∠DEB均为锐角，cos∠CEB＝cos∠DEB·cos∠CED＜cos∠DEB，即∠CEB＞∠DEB.

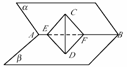
答案： A

2．二面角α－l－β的大小为锐角，P∈l，PA⊂α，PB⊂β且PA⊥l，则(　)

A．∠APB的最大值等于二面角的平面角

B．∠APB的最小值等于二面角的平面角

C．二面角的平面角既不是∠APB的最大值，也不是∠APB的最小值

D．∠APB就是二面角的平面角

解析：如右图，在平面β内作PC⊥l，则∠APC为二面角的平面角，cos∠APB＝cos∠BPC·cos∠APC≤cos∠APC，即∠APB≥∠APC，故选B.

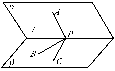
答案： B

1．设m、n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题，其中正确命题的序号是(　)

①若m⊥α，n∥α，则m⊥n；②若α∥β，β∥γ，m⊥α，则m⊥γ；③若m∥α，n∥α，则m∥n；④若α⊥γ，β⊥γ，则α∥β.

A．①和②　 B．②和③　 C．③和④　 D．①和④

答案：A

3．如下马图，四棱锥P-ABCD的底面是矩形，PA⊥平面ABCD，E、F分别是AB、PD的中点，又二面角P-CD-B为45°，

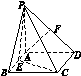
(1)求证：AF∥平面PEC；

(2)求证：平面PEC⊥平面PCD；

(3)设AD＝2，CD＝2，求点A到平面PEC的距离．

解答：(1)证明：取PC的中点G，连EG、FG，

∵F为PD的中点，∴GF綊CD，CD綊AB，又E为AB的中点，

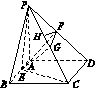
∴AE綊GF，∴四边形AEGF为平行四边形，∴AF∥GE，因此AF∥平面PEC.

(2)证明：PA⊥平面ABCD，则AD是PD在底面上的射影，又ABCD为矩形

∴CD⊥AD，则CD⊥PD，因此CD⊥AF，∠PDA为二面角P-CD-B的平面角，即∠PDA＝45°，F为Rt△PAD斜边PD的中点，AF⊥PD，PD∩CD＝D，

∴AF⊥平面PCD，由(1)知AF∥EG，∴EG⊥平面PDC，

∵EG⊂平面PEC，∴平面PEC⊥平面PCD.

(3)由(1)知AF∥平面PEC，平面PCD⊥平面PEC，过F作FH⊥PC交PC于H，则FH⊥平面PEC，∴FH为F到平面PEC的距离，即A到平面PEC的距离，在△PFH与△PCD中，∠P为公共角，

∠FHP＝∠CDP＝90°，∴△PFH∽△PCD，＝，

∵AD＝2，PF＝，PC＝＝＝4，

∴FH＝·2＝1，∴A到平面PEC的距离为1.

2．如图，已知平面α∥β∥γ，A，C∈α，B，D∈γ，异面直线AB和CD分别与β交于

E和G，连结AD和BC分别交β于F，H.

(1)求证：＝；

(2)判断四边形EFGH是哪一类四边形；

(3)若AC＝BD＝a，求四边形EFGH的周长．

解答：(1)证明：由AB，AD确定的平面，与平行平面β和γ的交线分别为EF和BD，

知EF∥BD.所以＝.同理有FG∥AC，因而＝.所以＝.

(2)面CBD分别交β，γ于HG和BD.由于β∥γ，所以HG∥BD.同理EH∥AC.故EFGH

为平行四边形．

(3)由EF∥BD，得＝＝.由FG∥AC，得＝＝.

又因为BD＝AC＝a，所以+＝＝＝1.即EF+FG＝a.

故四边形EFGH的周长为2a.

1．如果α∥β，AB和CD是夹在平面α与β之间的两条线段，AB⊥CD，且AB＝2，

直线AB与平面α所成的角为30°，那么线段CD的取值范围是(　)

A．(，]　 　　B．[1，+∞)　 　　C．[1，]　 　　D．[，+∞)

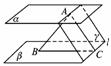
解析：如图，过A点作平面γ⊥AB，γ∩β＝l，过A作AC⊥l.

垂足为C，连结AC，可以证明AC即为线段CD的最小值．

在Rt△ABC中，∠ABC＝30°，AB＝2，

∴AC＝ABtan∠ABC＝.即CD≥.

答案：D

10．已知：如右图，平面α∥平面β，线段AB分别交α、β于点M、N，线段AD分别

交α、β于C、D，线段BF分别交α、β于F、E，且AM＝BN，试证：S_△CMF＝S_△DNE.

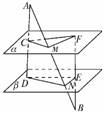
证明：∵α∥β，直线AD与AB确定的平面与α、β分别交于CM、DN，

∴CM∥DN，同理NE∥MF，∴∠CMF＝∠DNE，＝.＝，

又AM＝BN，∴＝，即CM·MF＝DN·NE，∴CM·MFsin∠CMF＝

DN·NEsin∠DNE.因此S_△CMF＝S_△DNE.

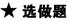
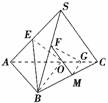
9．(原创题)如图在四面体S-ABC中，E、F、O分别为SA、SB、AC的中点，G为OC的中点，证明：FG∥平面BEO.

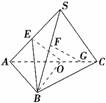
证明：证法一：如图，取BC中点M，连接FM，GM，则GM∥OB，FM∥SC∥EO，

又FM∩GM＝M，则平面FGM∥平面BEO，因此FG∥平面BEO.

证法二：设，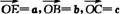

则＝＝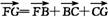

＝＝

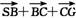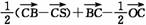
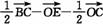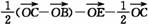
＝－＝－b－a，因此FG与b，a共面，∴FG∥平面BEO.

8．如下图，在正方体ABCD-A₁B₁C₁D₁中，M、N、P、Q分别为A₁D₁、A₁B₁、B₁C₁、C₁D₁的中点，求证：平面AMN∥平面PQDB.

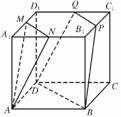
证明：如图连结NQ，由NQ綊A₁D₁綊AD知：四边形ADQN为平行四边形，则AN∥DQ；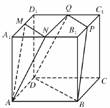

同理AM∥BP，又AM∩AN＝A，根据平面与平面平行的判定定理可知，平面AMN∥平面PQDB.