2．若{a、b、c}为空间的一组基底，则下列各项中，能构成基底的一组向量是(　)

A．a，a+b，a－b　 　　　　B．b，a+b，a－b　

C．c，a+b，a－b　 　　　　D．a+b，a－b，a+2b

解析：若c、a+b、a－b共面，则c＝λ(a+b)+m(a－b)＝(λ+m)a+(λ－m)b，则a、b、

c为共面向量，此与{a、b、c}为空间向量的一组基底矛盾，故c，a+b，a－b可构成空

间向量的一组基底．

答案：C

1．对于空间三个向量a、b、a+2b，它们一定是(　)

A．共线向量　 B．共面向量　 C．不共线向量　 D．不共面向量

答案：B

2．如下图，已知四棱锥P－ABCD，PB⊥AD，侧面PAD为边长等于2的正三角形，底面ABCD为菱形，侧面PAD与底面ABCD所成的二面角为120°.

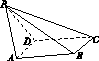
(1)求点P到平面ABCD的距离；

(2)求面APB与面CPB所成二面角的余弦值．

解答：(1)如下图，作PO⊥平面ABCD，

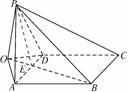
垂足为O，连结OB、OA、OD，OB与AD交于E，连结PE，

∵AD⊥PB，∴AD⊥OB，∵PA＝PD，∴OA＝OD，

于是OB平分AD，点E为AD的中点，∴PE⊥AD.

由此知∠PEB为面PAD与面ABCD所成二面角的平面角，

∴∠PEB＝120°，∠PEO＝60°.

由已知可求得PE＝，

∴PO＝PE·sin 60°＝×＝，即点P到平面ABCD的距离为.

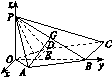
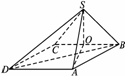
1．如图，四棱锥S－ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD.已知∠ABC＝45°，AB＝2，BC＝2，SA＝SB＝.

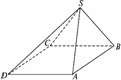
(1)证明SA⊥BC；

(2)求直线SD与平面SBC所成角的正弦值．

解答：(1)证明：作SO⊥BC，垂足为O，连结AO，由侧面SBC⊥底面ABCD，得SO⊥底面ABCD.

因为SA＝SB，所以AO＝BO.

又∠ABC＝45°，故△AOB为等腰直角三角形，AO⊥BO，由三垂线定理，得SA⊥BC.

(2)由(1)知SA⊥BC，依题设AD∥BC，故SA⊥AD，

由AD＝BC＝2，SA＝，AO＝，得SO＝1，SD＝.

△SAB的面积：S₁＝AB·＝.

连结DB，得△DAB的面积S₂＝AB·ADsin 135°＝2.

设D到平面SAB的距离为h，由V_D-SAB＝V_S-ABD，得h·S₁＝SO·S₂，

解得h＝.设SD与平面SAB所成角为α，则sin α＝＝＝.

所以，直线SD与平面SAB所成的角正弦值为.

10．如下图所示，在正方体ABCD－A₁B₁C₁D₁中，P是棱AD的中点，求二面角A－BD₁－P的大小．

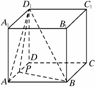
解答：∵AB⊥平面AD₁P，∴平面AD₁P⊥平面AD₁B.

过P作PE⊥AD₁垂足为E，

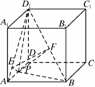
则PE⊥平面AD₁B，作EF⊥BD₁，连结PF，

则由三垂线定理知PF⊥BD₁，

则∠PFE为二面角A－BD₁－P的平面角，设AB＝1，

∵Rt△AEP∽Rt△ADD₁，＝∴PE＝＝，

在等腰△PBD₁中，BP＝，BF＝BD₁＝，

∴PF＝＝，在Rt△PEF中，sin∠PFE＝＝，∴∠PFE＝30°.

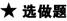
9．如右图，在四棱锥V－ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD，

(1)证明AB⊥平面VAD；

(2)求面VAD与面VBD所成的二面角的正切值．

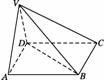
解答：(1)证明：∵平面VAD⊥底面ABCD，

又AB⊥AD，则AB⊥平面VAD.

(2)取VD中点E，连结AE、BE，

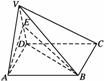
∵△VAD是正三角形，则AE⊥VD，由三垂线定理知BE⊥VD.

∴∠AEB为面VAD与面VBD所成二面角的平面角．

设AB＝1，在Rt△AED中，AE＝ADsin 60°＝，

∴tan∠AEB＝＝.

8．若P为△ABC所在平面外一点，且PA⊥平面ABC，平面PAC⊥平面PBC，求证：BC⊥AC.

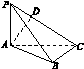
证明：∵平面PAC⊥平面PBC，作AD⊥PC垂足为D，

根据平面与平面垂直的性质定理知：AD⊥平面PBC，则BC⊥AD，

又PA⊥平面ABC，则BC⊥PA，∴BC⊥平面PAC.因此BC⊥AC.

7．已知P是△ABC所在平面α外一点，O是点P在平面α内的射影

(1)若P到△ABC的三个顶点的距离相等，则O是△ABC的__________；

(2)若PA、PB、PC与平面α所成的角相等，则O是△ABC的__________；

(3)若P到△ABC三边距离相等，且O在△ABC的内部，则O是△ABC的__________；

(4)若平面PAB、PBC、PCA与平面α所成的角相等，且O在△ABC的内部，则O是△ABC的__________；

(5)若PA、PB、PC两两垂直，则O是△ABC的________．

答案：(1)外心　(2)外心　(3)内心　(4)内心　(5)垂心

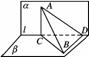
6．一条线段的两个端点分别在一个直二面角的两个面内，则这条线段与这两个平面所成的角的和的范围是________．

解析：作AC⊥l垂足为C，作BD⊥l垂足为D，连结BC、AD，

则∠BAD和∠ABC分别为直线AB和平面α和β所成角．

由cos∠ABD＝cos∠ABC·cos∠DBC≤cos∠ABC，

即∠ABD≥∠ABC，∠ABC+∠BAD≤∠ABD+∠BAD＝90°.

答案：(0°，90°]

5．α、β是两个不同的平面，m、n是平面α及β之外的两条不同的直线，给出四个论断：①m⊥n；②α⊥β；③n⊥β；④m⊥α，以其中三个论断作为条件，剩余的一个论断作为结论，写出你认为正确的一个命题____________．

答案：可填①③④⇒②与②③④⇒①中的一个