
2.如右图,已知M、N分别为四面体ABCD的面BCD与面ACD的重心,且G为AM
上一点,且GM∶GA=1∶3.
求证:B、G、N三点共线.

证明:设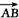 =a,
=a, =b,
=b,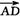 =c,则
=c,则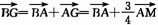 =-a+(a+b+c)=
=-a+(a+b+c)=
-a+b+c,
 =-a+b+c=BG.∴
=-a+b+c=BG.∴ ,即B、
,即B、
G、N三点共线.
1.已知向量{a,b,c}是空间的一组基底,向量{a+b,a-b,c}是空间的另一组基底,
一向量p在基底{a,b,c}下的坐标为(1,2,3),求在基底{a+b,a-b,c}下的坐标.
解答:设p在基底{a+b,a-b,c}下的坐标为(x, y, z),则a+2b+3c=x(a+b)+y(a-
b)+zc=(x+y)a+ (x-y)b+zc,∴解得
故p在基底{a+b,a-b,c}下的坐标为(,-,3).
10.如右图,在空间四边形SABC中,AC、BS为其对角线,O为△ABC的重心,试
证:

(1) ;(2)
;(2) 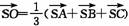 .
.
证明:(1) 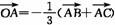 ,①
,①
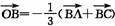 ,②
,②
 ,③
,③
①+②+③得 .
.
(2) 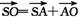 ,④
,④
 ,⑤
,⑤
 ,⑥
,⑥
由(1)得: .
.
④+⑤+⑥得3 即SO=(
即SO=(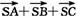 ).
).

9.求证:空间四边形对角线互相垂直的充要条件是对边平方和相等.
证明:设 =a,
=a, =b,
=b,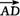 =c,充分性证明:则
=c,充分性证明:则 =a+b-c.
=a+b-c.
根据已知条件:a2+(a+b-c)2=b2+c2,整理得:a2+a·b-a·c-b·c=0,
即(a+b)·(a-c)=0,因此AC⊥BD.
必要性证明:∵(a+b)·(a-c)=0,∴a2+a·b-a·c-b·c=0.
即a2+(a+b-c)2=b2+c2,因此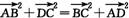 .
.
8.证明三个向量a=-e1+3e2+2e3,b=4e1-6e2+2e3,c=-3e1+12e2+11e3共面.
证明:若e1、e2、e3共面,显然a、b、c共面;若e1、e2、e3不共面,设c=λa+μb,
即-3e1+12e2+11e3=λ(-e1+3e2+2e3)+μ(4e1-6e2+2e3),
整理得-3e1+12e2+11e3=(4μ-λ)e1+(3λ-6μ)e2+(2λ+2μ)e3,
由空间向量基本定理可知
解得即c=5a+b,则三个向量共面.
7.下列命题中,正确的命题个数为________.
①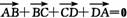 ;②|a|-|b|=|a+b|是a、b共线的充要条件;③若a与b共面,
;②|a|-|b|=|a+b|是a、b共线的充要条件;③若a与b共面,
则a与b所在的直线在同一平面内;④若 ,则P、A、B三点共线.
,则P、A、B三点共线.
答案:1
6.已知e1、e2、e3为不共面向量,若a=e1+e2+e3,b=e1-e2+e3,c=e1+e2-e3,
d=e1+2e2+3e3,且d=xa+yb+zc,则x、y、z分别为______________.
解析:由d=xa+yb+zc得e1+2e2+3e3=(x+y+z)e1+(x-y+z)e2+(x+y-z)e3,
∴解得:
答案:,-,-1
5.在下列条件中,使M与A、B、C一定共面的是________.
① ;②
;② ;
;
③ ; ④
; ④ ;
;
解析:∵ ,∴
,∴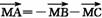 ,则
,则 、
、 、
、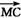 为共面向量,
为共面向量,
即M、A、B、C四点共面.
答案:③
4.以下四个命题中正确的是( )
A.空间的任何一个向量都可用其他三个向量表示
B.若{a、b、c}为空间向量的一组基底,则{a+b,b+c,c+a}构成空间向量的另一组
基底
C.△ABC为直角三角形的充要条件是 =0
=0
D.任何三个不共线的向量都可构成空间向量的一组基底
解析:若a+b、b+c、c+a为共面向量,则a+b=λ(b+c)+μ(c+a),(1-μ)a=(λ-1)b
+(λ+μ)c,λ、μ不可能同时为1,设μ≠1,则a= b+c,则a、b、c为共
面向量,此与{a、b、c}为空间向量基底矛盾.
答案:B
3.P为正六边形ABCDEF外一点,O为ABCDEF的中心,则
 等于( )
等于( )
A. B.3
B.3 C.6
C.6 D.0
D.0
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com