
8. (陕西长安二中2008届高三第一学期第二次月考)为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形
(陕西长安二中2008届高三第一学期第二次月考)为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形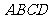 上规划出一块长方形地面建造公园,公园一边落在CD 上,但不得越过文物保护区
上规划出一块长方形地面建造公园,公园一边落在CD 上,但不得越过文物保护区 的EF.问如何设计才能使公园占地面积最大,并求这最大面积( 其中AB=200 m,BC=160 m,AE=60 m,AF=40 m.)
的EF.问如何设计才能使公园占地面积最大,并求这最大面积( 其中AB=200 m,BC=160 m,AE=60 m,AF=40 m.)
解 设CG=x,矩形CGPH面积为y,
如图作EN⊥PH于点N,则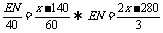
∴HC=160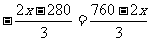
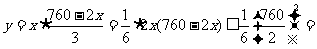
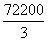
当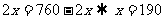 (m)即CG长为190m时,最大面积为
(m)即CG长为190m时,最大面积为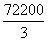 (m2)
(m2)
7.(四川省成都市新都一中高2008级一诊适应性测试)某机床厂今年年初用98万元购进一台
数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值);
(3)使用若干年后,对机床的处理方案有两种:(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
解 (1)依题得: (x
(x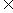 N*)
N*)
(2)解不等式
∵x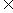 N*,∴3≤x≤17,故从第3年开始盈利。
N*,∴3≤x≤17,故从第3年开始盈利。
(3)(Ⅰ)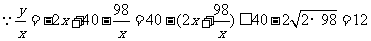
当且仅当 时,即x=7时等号成立.
时,即x=7时等号成立.
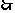 到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.
到2008年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.
(Ⅱ)y=-2x2+40x-98=-(x-10)2+102,当x=10时,ymax=102
故到2011年,盈利额达到最大值,工厂获利102+12=114万元
盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理.
6.( 2008年高考数学各校月考试题)某公司以每吨10万元的价格销售某种化工产品,每年可售出该产品1000吨,若将该产品每吨的价格上涨x%,则每年的销售数量将减少mx%,其中m为正常数.
(1)当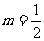 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
(2)如果涨价能使销售总金额增加,求m的取值范围.
解(1)由题设,当价格上涨x%时,销售总金额为:
(2)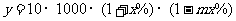 (万元)
(万元)
即 。
。
当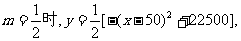
当x=50时,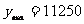 万元.
万元.
即该吨产品每吨的价格上涨50%时,销售总最大.
(2)由(1)
如果上涨价格能使销假售总金额增加,
则有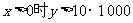
即x>0时,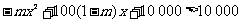
∴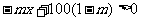
注意到m>0
∴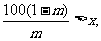 ∴
∴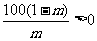 ∴
∴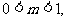
∴m的取值范围是(0,1)
5.(2007年岳阳市一中训练)某工厂统计资料显示,产品次品率p与日产量n (件)(n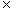 N*,且1≤n≤98)的关系表如下:
N*,且1≤n≤98)的关系表如下:
|
N |
1 |
2 |
3 |
4 |
┅ |
98 |
|
P |
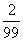 |
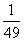 |
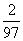 |
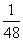 |
┅ |
1 |
又知每生产一件正品盈利a元,每生产一件次品损失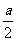 元(
元( ).
).
(1)将该厂日盈利额T(元)表示为日产量n (件)的一种函数关系式;
(2)为了获得最大盈利,该厂的日产量应定为多少件?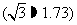
解 (1)由题意可知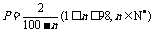 日产量n 件中,正品(n-pn)件,日盈利额
日产量n 件中,正品(n-pn)件,日盈利额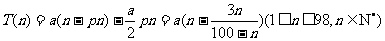 .
.
(2)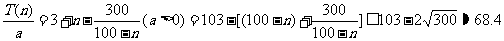
当且仅当100-n=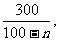 即n=100-
即n=100-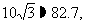 而
而 ,且
,且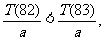
故 时
时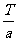 取最大值,即
取最大值,即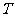 取最大值.
取最大值.
4.(四川省成都市新都一中高2008级12月月考)在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y=f(x),一种是平均价格曲线y=g(x)(如f(2)=3表示开始交易后第2小时的即时价格为3元;g(2)=4表示开始交易后两个小时内所有成交股票的平均价格为4元).下面所给出的四个图象中,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是 ( )

A B C D
答案 C
解析 刚开始交易时,即时价格和平均价格应该相等,A错误;开始交易后,平均价格应该跟随即使价格变动,在任何时刻其变化幅度应该小于即时价格变化幅度,B、D均错误.
3.(2008年全国百校月考) 用二分法研究函数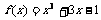 的零点时,第一次经计算
的零点时,第一次经计算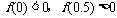 ,可得其中一个零点
,可得其中一个零点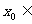 ,第二次应计算 . 以上横线上应填的内容为
,第二次应计算 . 以上横线上应填的内容为
A.(0,0.5), B.(0,1),
B.(0,1),
C.(0.5,1),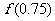 D.(0,0.5),
D.(0,0.5),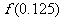
答案 A
2.(四川省成都市新都一中高2008级一诊适应性测试)如果二次方程x2-px-q=0(p,q∈N*) 的正根小于3, 那么这样的二次方程有 ( )
A. 5个 B. 6个 C. 7个 D. 8个 答案 C
1.(广东省惠州市2008届高三第三次调研考试)若函数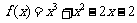 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
|
f (1) = -2 |
f (1.5) = 0.625 |
f (1.25) = -0.984 |
|
f (1.375) = -0.260 |
f (1.4375) = 0.162 |
f (1.40625) = -0.054 |
那么方程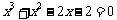 的一个近似根(精确到0.1)为 ( )
的一个近似根(精确到0.1)为 ( )
A.1.2 B.1.3 C.1.4 D.1.5
答案 C
解析 f(1.40625)=-0.054< 0,f(1.4375)=0.162> 0 且都接近0,由二分法可知其根近似于1.4。
9.(2009福建省)已知某企业原有员工2000人,每人每年可为企业创利润3.5万元.为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的5%,并且每年给每位待岗员工发放生活补贴O.5万元.据评估,当待岗员工人数x不超过原有员工1%时,留岗员工每人每年可为企业多创利润(1-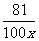 )万元;当待岗员工人数x超过原有员工1%时,留岗员工每人每年可为企业多创利润O.9595万元.为使企业年利润最大,应安排多少员工待岗?
)万元;当待岗员工人数x超过原有员工1%时,留岗员工每人每年可为企业多创利润O.9595万元.为使企业年利润最大,应安排多少员工待岗?
解 设重组后,该企业年利润为y万元.
∵2000×1%=20,∴当0<x≤20且x∈N时,
y=(2000-x)(3.5+1-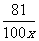 )-0.5x=-5(x+
)-0.5x=-5(x+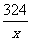 )+9000.81.
)+9000.81.
∵x≤2000×5% ∴x≤100,∴当20<x≤100且x∈N时,
y=(2000-x)(3.5+0.9595)-0.5x=-4.9595x+8919.
∴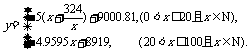
当0<x≤20时,有
y=-5(x+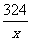 )+9000.81≤-5×2
)+9000.81≤-5×2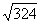 +9000.81=8820.81,
+9000.81=8820.81,
当且仅当x=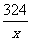 ,即x=18时取等号,此时y取得最大值.
,即x=18时取等号,此时y取得最大值.
当20<x≤100时,函数y=-4.9595x+8919为减函数,
所以y<-4.9595×20+8919=8819.81.
综上所述x=18时,y有最大值8820.81万元.
即要使企业年利润最大,应安排18名员工待岗.
2007-2008年联考题
8.(2009福州八中)某造船公司年造船量是20艘,已知造船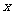 艘的产值函数为R(x)=3700x+45x2-10x3(单位:万元),成本函数为C(x)=460x+5000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x)。
艘的产值函数为R(x)=3700x+45x2-10x3(单位:万元),成本函数为C(x)=460x+5000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x)。
(Ⅰ)求利润函数P(x)及边际利润函数MP(x);(提示:利润=产值成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数MP(x)单调递减时x的取值范围,并说明单调递减在本题中的实际意义是什么?
解 (Ⅰ)P(x)=R(x)-C(x)=-10x3+45x2+3240x-5000,(x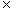 N*,且1≤x≤20); MP(x)=P(x+1)-P(x)=-30x2+60x+3275,(x
N*,且1≤x≤20); MP(x)=P(x+1)-P(x)=-30x2+60x+3275,(x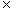 N*,且1≤x≤19)
N*,且1≤x≤19)
(Ⅱ)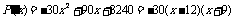 .
.
∴当0<x<12时 >0,当x<12时,
>0,当x<12时, <0.
<0.
∴x=12,P(x)有最大值.
即年造船量安排12 艘时,可使公司造船的年利润最大.
(Ⅲ)∵MP(x)=-30x2+60x+3275=-30(x-1)2+3305,
所以,当x≥1时,MP(x)单调递减,x的取值范围为[1,19],且x N*
N*
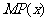 是减函数的实际意义:随着产量的增加,每艘船的利润在减少.
是减函数的实际意义:随着产量的增加,每艘船的利润在减少.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com