
3.(2010湖北理)17.(本小题满分12分)
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。


2009年高考题
2.(2010四川文)(22)(本小题满分14分)
设 (
( 且
且 ),g(x)是f(x)的反函数.
),g(x)是f(x)的反函数.
(Ⅰ)求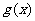 ;
;
(Ⅱ)当 时,恒有
时,恒有 成立,求t的取值范围;
成立,求t的取值范围;
(Ⅲ)当0<a≤时,试比较f(1)+f(2)+…+f(n)与 的大小,并说明理由.
的大小,并说明理由.



1.(2010四川理)(22)(本小题满分14分)
设 (
( 且
且 ),g(x)是f(x)的反函数.
),g(x)是f(x)的反函数.
(Ⅰ)设关于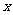 的方程求
的方程求 在区间[2,6]上有实数解,求t的取值范围;
在区间[2,6]上有实数解,求t的取值范围;
(Ⅱ)当a=e(e为自然对数的底数)时,证明: ;
;
(Ⅲ)当0<a≤时,试比较 与4的大小,并说明理由.
与4的大小,并说明理由.
本小题考产函数、反函数、方程、不等式、导数及其应用等基础知识,考察化归、分类整合等数学思想方法,以及推理论证、分析与解决问题的能力.
解:(1)由题意,得ax=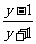 >0
>0
故g(x)= ,x∈(-∞,-1)∪(1,+∞)
,x∈(-∞,-1)∪(1,+∞)
由 得
得
t=(x-1)2(7-x),x∈[2,6]
则t'=-3x2+18x-15=-3(x-1)(x-5)
列表如下:
|
x |
2 |
(2,5) |
5 |
(5,6) |
6 |
|
t' |
|
+ |
0 |
- |
|
|
t |
5 |
↗ |
极大值32 |
↘ |
25 |
所以t最小值=5,t最大值=32
所以t的取值范围为[5,32]……………………………………………………5分
(2) 
=ln( )
)
=-ln
令u(z)=-lnz2- =-2lnz+z-
=-2lnz+z- ,z>0
,z>0
则u'(z)=- =(1-
=(1- )2≥0
)2≥0
所以u(z)在(0,+∞)上是增函数
又因为 >1>0,所以u(
>1>0,所以u( )>u(1)=0
)>u(1)=0
即ln >0
>0
即 ………………………………………………………………9分
………………………………………………………………9分
(3)设a= ,则p≥1,1<f(1)=
,则p≥1,1<f(1)= ≤3
≤3
当n=1时,|f(1)-1|= ≤2<4
≤2<4
当n≥2时
设k≥2,k∈N *时,则f(k)=
=1+
所以1<f(k)≤1+
从而n-1<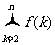 ≤n-1+
≤n-1+ =n+1-
=n+1- <n+1
<n+1
所以n< <f(1)+n+1≤n+4
<f(1)+n+1≤n+4
综上所述,总有| -n|<4
-n|<4
1.(2010上海文)9.函数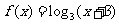 的反函数的图像与
的反函数的图像与 轴的交点坐标是
。
轴的交点坐标是
。
答案 (0,-2)
解析:考查反函数相关概念、性质
法一:函数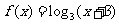 的反函数为
的反函数为 ,另x=0,有y=-2
,另x=0,有y=-2
法二:函数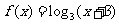 图像与x轴交点为(-2,0),利用对称性可知,函数
图像与x轴交点为(-2,0),利用对称性可知,函数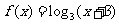 的反函数的图像与
的反函数的图像与 轴的交点为(0,-2)
轴的交点为(0,-2)
15.(2010安徽理)6、设 ,二次函数
,二次函数 的图象可能是
的图象可能是

答案 D
[解析]当 时,
时,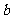 、
、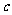 同号,(C)(D)两图中
同号,(C)(D)两图中 ,故
,故 ,选项(D)符合.
,选项(D)符合.
[方法技巧]根据二次函数图像开口向上或向下,分 或
或 两种情况分类考虑.另外还要注意c值是抛物线与y轴交点的纵坐标,还要注意对称轴的位置或定点坐标的位置等.
两种情况分类考虑.另外还要注意c值是抛物线与y轴交点的纵坐标,还要注意对称轴的位置或定点坐标的位置等.
14.(2010四川文)(2)函数y=log2x的图象大致是
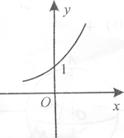



(A) (B) (C) (D)
答案 C
解析:本题考查对数函数的图象和基本性质.
13.(2010全国卷1文)(7)已知函数 .若
.若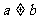 且,
且, ,则
,则 的取值范围是
的取值范围是
(A) (B)
(B) (C)
(C)
 (D)
(D) 
答案 C
[命题意图]本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a的取值范围,而利用均值不等式求得a+b= ,从而错选D,这也是命题者的用苦良心之处.
,从而错选D,这也是命题者的用苦良心之处.
[解析1]因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或 ,所以a+b=
,所以a+b=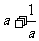
又0<a<b,所以0<a<1<b,令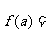
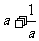 由“对勾”函数的性质知函数
由“对勾”函数的性质知函数 在
在 (0,1)上为减函数,所以f(a)>f(1)=1+1=2,即a+b的取值范围是(2,+∞).
(0,1)上为减函数,所以f(a)>f(1)=1+1=2,即a+b的取值范围是(2,+∞).
[解析2]由0<a<b,且f(a)=f(b)得: ,利用线性规划得:
,利用线性规划得: ,化为求
,化为求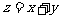 的取值范围问题,
的取值范围问题, ,
, 过点
过点 时z最小为2,∴(C)
时z最小为2,∴(C) 
12.(2010天津文)(6)设
(A)a<c<b (B) )b<c<a (C) )a<b<c (D) )b<a<c
答案 D
[解析]本题主要考查利用对数函数的单调性比较大小的基本方法,属于容易题。
因为
[温馨提示]比较对数值的大小时,通常利用0,1进行,本题也可以利用对数函数的图像进行比较。
11.(2010四川理)(3)2log510+log50.25=
(A)0 (B)1 (C) 2 (D)4
解析:2log510+log50.25
=log5100+log50.25
=log525
=2
答案 C
10.(2010北京文)⑷若a,b是非零向量,且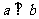 ,
, ,则函数
,则函数 是
是
(A)一次函数且是奇函数 (B)一次函数但不是奇函数
(C)二次函数且是偶函数 (D)二次函数但不是偶函数
答案 A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com