
7.(2009厦门十中)定义:若存在常数 ,使得对定义域
,使得对定义域 内的任意两个
内的任意两个 ,
,
均有 成立,则称函数
成立,则称函数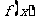 在定义域
在定义域 上满足利普希茨条件。若函数
上满足利普希茨条件。若函数 满足利普希茨条件,则常数
满足利普希茨条件,则常数 的最小值为_____。
的最小值为_____。
答案
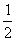
6.(2009泉州市)已知函数f(x)= 若f(a)=
若f(a)=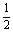 .
.
答案 -1或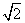
5.(2009岳阳一中第四次月考)函数 的图象大致是 ( )
的图象大致是 ( )

答案 D
4.(2009厦门集美中学)若 在
在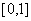 上是减函数,则
上是减函数,则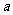 的取值范围
的取值范围
是 ( )
A. B.
B.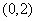 C.
C. D.
D.
答案 C
3.(2009福建省)函数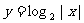 的图象大致是 ( )
的图象大致是 ( )

答案 C
2. (北京市朝阳区2009年4月高三一模理)下列函数中,在区间 上为增函数的
上为增函数的
是 ( )
A. B.
B.
C. D.
D.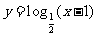
答案 B
1.(2009年4月北京海淀区高三一模文)函数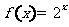 的反函数
的反函数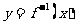 的图象
的图象
是 ( )
答案 A
9、(2009湛江一模)已知函数 .(
.( )
)
(Ⅰ)当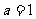 时,求
时,求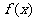 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数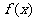 的图象恒在直线
的图象恒在直线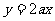 下方,求
下方,求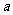 的取值范围.
的取值范围.
解:(Ⅰ)当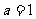 时,
时, ,
, ;………………2分
;………………2分
对于 [1,e],有
[1,e],有 ,∴
,∴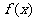 在区间[1,e]上为增函数,…………3分
在区间[1,e]上为增函数,…………3分
∴ ,
,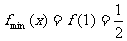 .……………………………5分
.……………………………5分
(Ⅱ)令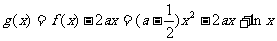 ,则
,则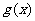 的定义域为(0,+∞).
的定义域为(0,+∞).
……………………………………………6分
在区间(1,+∞)上,函数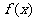 的图象恒在直线
的图象恒在直线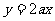 下方等价于
下方等价于 在区间(1,+∞)上恒成立.
在区间(1,+∞)上恒成立.
∵
① 若 ,令
,令 ,得极值点
,得极值点 ,
, ,………………8分
,………………8分
当 ,即
,即 时,在(
时,在(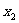 ,+∞)上有
,+∞)上有 ,
,
此时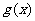 在区间(
在区间(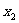 ,+∞)上是增函数,并且在该区间上有
,+∞)上是增函数,并且在该区间上有
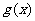 ∈(
∈( ,+∞),不合题意;………………………………………9分
,+∞),不合题意;………………………………………9分
当 ,即
,即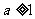 时,同理可知,
时,同理可知,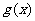 在区间(1,+∞)上,有
在区间(1,+∞)上,有
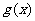 ∈(
∈( ,+∞),也不合题意;………………………………………10分
,+∞),也不合题意;………………………………………10分
② 若 ,则有
,则有 ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有 ,
,
从而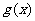 在区间(1,+∞)上是减函数;……………………………………12分
在区间(1,+∞)上是减函数;……………………………………12分
要使 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足
 ,
,
由此求得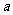 的范围是[
的范围是[ ,
,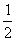 ].
].
综合①②可知,当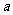 ∈[
∈[ ,
,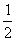 ]时,函数
]时,函数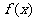 的图象恒在直线
的图象恒在直线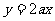 下方.
下方.
………………………………………………14分
2009年联考题
8、(2009深圳一模)已知函数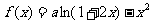 (
( ,
,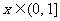 ).
).
(Ⅰ)求函数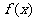 的单调递增区间;
的单调递增区间;
(Ⅱ)若不等式 对一切正整数
对一切正整数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
解:(Ⅰ) …………………
2分
…………………
2分
 ,
,
由 ,得
,得 .
.
 ,
, ,
, .
.
又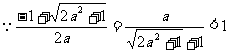 .
.
 函数
函数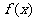 的单调递增区间为
的单调递增区间为 ,递减区间为
,递减区间为 . ………… 6分
. ………… 6分
(Ⅱ)[法一]不等式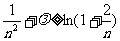 ,即为
,即为 .……………(※)
.……………(※)
令 ,当
,当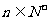 时,
时,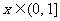 .
.
则不等式(※)即为 .
…………………9分
.
…………………9分
令 ,
, ,
,
 在
在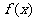 的表达式中,当
的表达式中,当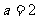 时,
时,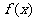
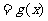 ,
,
又
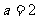 时,
时,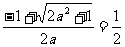 ,
,

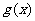 在
在 单调递增,在
单调递增,在 单调递减.
单调递减.
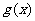 在
在 时,取得最大,最大值为
时,取得最大,最大值为 . …………………12分
. …………………12分
因此,对一切正整数 ,当
,当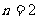 时,
时, 取得最大值
取得最大值 .
.
 实数
实数 的取值范围是
的取值范围是 . ………………………… 14分
. ………………………… 14分
[法二]不等式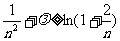 ,即为
,即为 .………………(※)
.………………(※)
设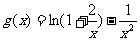
 ,
,
 ,
,
令 ,得
,得 或
或 .
………………………… 10分
.
………………………… 10分
 当
当 时,
时, ,当
,当 时,
时, .
.
 当
当 时,
时,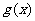 取得最大值
取得最大值 .
.
因此,实数 的取值范围是
的取值范围是 .
………………………… 14分
.
………………………… 14分
7、
解: (1)  ,两边加
,两边加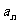 得:
得:  ,
,
 是以2为公比,
是以2为公比,  为首项的等比数列.
为首项的等比数列. 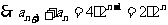 ……①
……①
由 两边减
两边减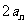 得:
得: 
 是以
是以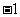
为公比,  为首项的等比数列.
为首项的等比数列.  ……②
……②
①-②得:  所以,所求通项为
所以,所求通项为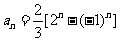 …………5分
…………5分
(2) 当 为偶数时,
为偶数时,

当 为奇数时,
为奇数时, ,
, ,又
,又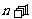 为偶数
为偶数
 由(1)知,
由(1)知,  ……………………10分
……………………10分
(3)证明:

又
 ……12分
……12分
 …………14分
…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com