
A∩B={x|x∈A,且x∈B}
――是同时属于A,B的两个集合的所有元素组成的集合.
A∪B={x|x∈A或x∈B}
――是属于A或者属于B的元素所组成的集合.
1.课本P12练习(1-5) 2.课本P13 练习(1-4)
例1 设A={x|x>-2},B={x|x<3},求A B.
B.
解:A B={x|x>-2}
B={x|x>-2} {x|x<3}={x|-2<x<3}.
{x|x<3}={x|-2<x<3}.
例2 设A={x|x是等腰三角形},B={x|x是直角三角形},求A B.
B.
解:A B={x|x是等腰三角形}
B={x|x是等腰三角形} {x|x是直角三角形}
{x|x是直角三角形}
={x|x是等腰直角三角形}.
例3 A={4,5,6,8},B={3,5,7,8},求A B.
B.
解:A B={3,4,5,6,7,8}.
B={3,4,5,6,7,8}.
例4设A={x|x是锐角三角形},B={x|x是钝角三角形},求A B.
B.
解:A B={x|x是锐角三角形}
B={x|x是锐角三角形} {x|x是钝角三角形}
{x|x是钝角三角形}
={x|x是斜三角形}.
例5设A={x|-1<x<2},B={x|1<x<3},求A∪B.
解:A B={x|-1<x<2}
B={x|-1<x<2} {x|1<x<3}={x|-1<x<3}.
{x|1<x<3}={x|-1<x<3}.
说明:求两个集合的交集、并集时,往往先将集合化简,两个数集的交集、并集,可通过数轴直观显示;利用韦恩图表示两个集合的交集,有助于解题
例6(课本第12页)设A={(x,y)|y=-4x+6},{(x,y)|y=5x-3},求A B.
B.
解:A B={(x,y)|y=-4x+6}
B={(x,y)|y=-4x+6} {(x,y)|y=5x-3}
{(x,y)|y=5x-3}
={(x,y)|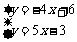 }={(1,2)}
}={(1,2)}
注:本题中,(x,y)可以看作是直线上的的坐标,也可以看作二元一次方程的一个解.
形如2n(n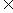 Z)的整数叫做偶数,形如2n+1(n
Z)的整数叫做偶数,形如2n+1(n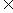 Z)的数叫做奇数,全体奇数的集合叫做奇数集全体偶数的集合叫做偶数集.
Z)的数叫做奇数,全体奇数的集合叫做奇数集全体偶数的集合叫做偶数集.
例7(课本第12页)已知A是奇数集,B是偶数集,Z为整数集,
求A B,A
B,A Z,B
Z,B Z,A
Z,A B,A
B,A Z,B
Z,B Z.
Z.
备用例题
例8设集合A={-4,2m-1,m2},B={9,m-5,1-m},又A B={9},
B={9},
求实数m的值.
解:∵A B={9},A={-4,2m-1,m2},B={9,m-5,1-m},
B={9},A={-4,2m-1,m2},B={9,m-5,1-m},
∴2m-1=9或m2=9,解得m=5或m=3或m=-3.
若m=5,则A={-4,9,25},B={9,0,-4}与A B={9}矛盾;
B={9}矛盾;
若m=3,则B中元素m-5=1-m=-2,与B中元素互异矛盾;
若m=-3,则A={-4,-7,9},B={9,-8,4}满足A B={9}.∴m=-3.
B={9}.∴m=-3.
例10.设A={x|x2+ax+b=0},B={x|x2+cx+15=0},又A B={3,5},A∩B={3},求实数a,b,c的值.
B={3,5},A∩B={3},求实数a,b,c的值.
解:∵A∩B={3},∴3∈B,∴32+3c+15=0,
∴c=-8.由方程x2-8x+15=0解得x=3或x=5,
∴B={3,5}.由A (A
(A B={3,5}知,
B={3,5}知,
3∈A,5 A(否则5∈A∩B,与A∩B={3}矛盾)
A(否则5∈A∩B,与A∩B={3}矛盾)
故必有A={3},∴方程x2+ax+b=0有两相同的根3,
由韦达定理得3+3=-a,3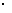 3=b,即a=-6,b=9,c=-8.
3=b,即a=-6,b=9,c=-8.
2.并集的定义
一般地,由所有属于集合A或属于集合B的元素所组成的集合,叫做A,B的并集.
记作:A B(读作‘A并B’),
B(读作‘A并B’),
即A B
={x|x
B
={x|x A,或x
A,或x B}).
B}).
如:{1,2,3,6} {1,2,5,10}={1,2,3,5,6,10}.
{1,2,5,10}={1,2,3,5,6,10}.
1.交集的定义
一般地,由所有属于A且属于B的元素所组成的集合,叫做A,B的交集.
记作A B(读作‘A交B’),
B(读作‘A交B’),
即A B={x|x
B={x|x A,且x
A,且x B}.
B}.
如:{1,2,3,6} {1,2,5,10}={1,2}.
{1,2,5,10}={1,2}.
又如:A={a,b,c,d,e},B={c,d,e,f}.则A B={c,d,e}.
B={c,d,e}.
4.观察下面两个图的阴影部分,它们同集合A、集合B有什么关系?

如上图,集合A和B的公共部分叫做集合A和集合B的交(图1的阴影部分),集合A和B合并在一起得到的集合叫做集合A和集合B的并(图2的阴影部分).
观察问题3中A、B、C三个集合的元素关系易知,集合C={1,2}是由所有属于集合A且属于集合B的元素所组成的,即集合C的元素是集合A、B的公共元素,此时,我们就把集合C叫做集合A与B的交集,这是今天我们要学习的一个重要概念.
问题:观察下列两组集合,说出集合A与集合B的关系(共性)
(1)A={1,2,3},B={1,2,3,4,5}
(2)A=N,B=Q
(3)A={-2,4},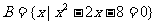
(集合A中的任何一个元素都是集合B的元素)
3.已知6的正约数的集合为A={1,2,3,6},10的正约数为B={1,2,5,10},那么6与10的正公约数的集合为C= .(答:C={1,2})
1.说出 的意义
2.填空:若全集U={x|0≤x<6,X∈Z},A={1,3,5},B={1,4},那么
的意义
2.填空:若全集U={x|0≤x<6,X∈Z},A={1,3,5},B={1,4},那么
 {0,2,4}
{0,2,4} 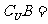 {0,2,3,5}
{0,2,3,5}
8.(江苏省启东中学2008年高三综合测试一)已知函数
(1)求反函数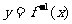
(2)判断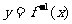 是奇函数还是偶函数并证明。
是奇函数还是偶函数并证明。
解 (1)令 则
则
∵t2-2yt-1=0
∴t=y+
∵10x=y+ w.w.
w.w.
∴f-1(x)=lg(x+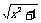 )(x
)(x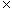 R)
R)
(2)
= =-lg(x+
=-lg(x+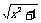 )=-f-1(x)
)=-f-1(x)
 为奇函数
为奇函数
7.(陕西长安二中2008届高三第一学期第二次月考)定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)f(b),
(1)求证:f(0)=1;
(2)求证:对任意的x∈R,恒有f(x)>0;
(3)证明:f(x)是R上的增函数;(4)若f(x)·f(2x-x2)>1,求x的取值范围。
解 (1)令a=b=0,则f(0)=[f(0)]2∵f(0)≠0 ∴f(0)=1
(2)令a=x,b=-x则 f(0)=f(x)f(-x) ∴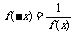
由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0
∴ 又x=0时,f(0)=1>0
又x=0时,f(0)=1>0
∴对任意x∈R,f(x)>0
(3)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0
∴
∴f(x2)>f(x1) ∴f(x)在R上是增函数
(4)f(x)·f(2x-x2)=f[x+(2x-x2)]=f(-x2+3x)又1=f(0),
f(x)在R上递增
∴由f(3x-x2)>f(0)得:3x-x2>0 ∴ 0<x<3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com