
3.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是( )
A. 4 B. 5 C. 6 D. 7
2.把589化成七进制数的末位为:( )
A. 1 B. 3 C. 5 D. 7
1.若三个点P(1,1),A(2,-4),B(x,-9)共线,则x=( )
A. -1 B. 3 C . D. 51
(三)解答题:
13、(07江苏)某气象站天气预报的准确率为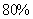 ,计算(结果保留到小数点后第2位):
,计算(结果保留到小数点后第2位):
(1)5次预报中恰有2次准确的概率;(4分)
(2)5次预报中至少有2次准确的概率;(4分)
(3)5次预报中恰有2次准确,且其中第3次预报准确的概率.(4分)
14、(04全国Ⅲ)已知8个球队中有3个弱队,以抽签方式将这8个球队分为A、B两组,每组4个.求 :(Ⅰ)A、B两组中有一组恰有两个弱队的概率;(Ⅱ)A组中至少有两个弱队的概率.
(二)填空题:
7、(07广东)甲、乙两个袋中装有红、白两种颜色的小球,这些小球除颜色外完全相同,其中甲袋装有4个红球,2个白球,乙袋装有1个红球,5个白球.现分别从甲、乙两袋中各随机取出一个球,则取出的两球都是红球的概率为 .(答案用分数表示)
8、(07湖北)某篮球运动员在三分线投球的命中率是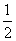 ,他投球10次,恰好投进3个球的概率 .(用数值作答)
,他投球10次,恰好投进3个球的概率 .(用数值作答)
9、(07上海)在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目 若选到男教师的概率为
若选到男教师的概率为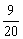 ,则参加联欢会的教师共有
人
,则参加联欢会的教师共有
人
10、(05重庆)某轻轨列车有4节车厢,现有6位乘客准备乘坐,设每一位乘客进入每节车厢是等可能的,则这6位乘客进入各节车厢的人数恰好为0,1,2,3的概率为 .
11、(04上海)若在二项式(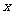 +1)10的展开式中任取一项,则该项的系数为奇数的概率是 ;
+1)10的展开式中任取一项,则该项的系数为奇数的概率是 ;
(结果用分数表示)
12、(04广东)某班委会由4名男生与3名女生组成,现从中选出2人担任正副班长,其中至少有1名女生当选的概率是 (用分数作答)。
(一)选择题:
1、(07江西)将一骰子连续抛掷三次,它落地时向上的点数依次成等差数列的概率为( )
 A、
A、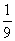 B、
B、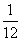 C、
C、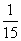 D、
D、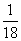
2、(06江苏)右图中有一个信号源和五个接收器。接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号。若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所有六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是( )
A、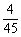 B、
B、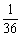 C、
C、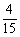 D、
D、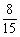
3、(06江西)将7个人(含甲、乙)分成三个组,一组3人,另两组2 人,不同的分组数为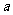 ,甲、乙分到同一组的概率为
,甲、乙分到同一组的概率为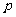 ,则
,则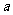 、
、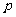 的值分别为( )
的值分别为( )
A、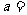 105
105 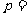
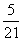 B、
B、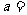 105
105 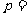
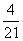
C、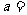 210
210 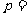
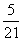 D、
D、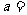 210
210 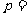
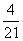
4、(05广东)先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为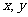 ,则
,则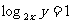 的概率为 ( )
的概率为 ( )
A、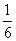 B、
B、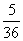 C、
C、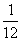 D、
D、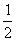
5、(05山东9)10张奖券中只有3张有奖,5个人购买,至少有1人中奖的概率是( )
A、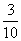 B、
B、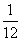 C、
C、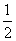 D、
D、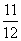
6、(04辽宁)甲、乙两人独立地解同一问题,甲解决这个问题的概率是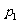 ,乙解决这个问题的概率是
,乙解决这个问题的概率是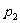 ,那么恰好有1人解决这个问题的概率是( )
,那么恰好有1人解决这个问题的概率是( )
A、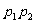 B、
B、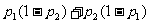
C、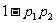 D、
D、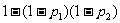
例1、(08上海春)古代“五行”学说认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,设事件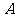 表示“排列中属性相克的两种物质不相邻”,则事件
表示“排列中属性相克的两种物质不相邻”,则事件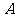 出现的概率是
(结果用数值表示);
出现的概率是
(结果用数值表示);
例2、(07山东)位于坐标原点的一个质点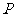 按下列规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是
按下列规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是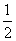 ,质点
,质点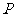 移动五次后位于点
移动五次后位于点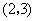 的概率是( )
的概率是( )
A、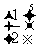 B、
B、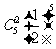 C、
C、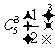 D、
D、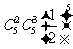
例3、(06四川)从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,这个数不能被3整除的概率为( )
A、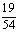 B、
B、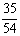 C、
C、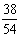 D、
D、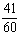
例4、(05湖北)以平行六面体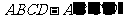 的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率
的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率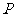 为( )
为( )
A、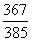 B、
B、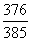 C、
C、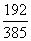 D、
D、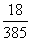
例5、(06湖南17)某安全生产监督部门对5家小型煤矿进行安全检查(简称安检), 若安检不合格, 则必须整改. 若整改后经复查仍不合格,
则强制关闭. 设每家煤矿安检是否合格是相互独立的, 且每家煤矿整改前合格的概率是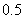 , 整改后安检合格的概率是
, 整改后安检合格的概率是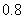 ,
,
计算(结果精确到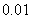 );
);
(Ⅰ) 恰好有两家煤矿必须整改的概率;
(Ⅱ) 平均有多少家煤矿必须整改;
(Ⅲ) 至少关闭一家煤矿的概率 .
例6、(05江苏20)甲、乙两人各射击一次,击中目标的概率分别是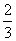 和
和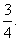 假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
(Ⅰ)求甲射击4次,至少1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
(三)解答题:
7、(06湖北)在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布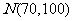 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)、试问此次参赛学生总数约为多少人?
(Ⅱ)、若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
可共查阅的(部分)标准正态分布表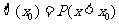
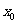 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1.2 1.3 1.4 1.9 2.0 2.1 |
0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 |
0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 |
0.888 0.9066 0.9222 0.9726 0.9783 0.9830 |
0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 |
0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 |
0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 |
0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 |
0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 |
0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 |
0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
解:(Ⅰ)设参赛学生的分数为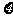 ,因为
,因为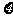 -N(70,100),由条件知,
-N(70,100),由条件知,
P(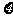 ≥90)=1-P(
≥90)=1-P(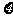 <90)=1-F(90)=1-
<90)=1-F(90)=1-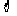
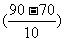 =1-
=1-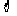 (2)=1-0.9772=0.228.
(2)=1-0.9772=0.228.
这说明成绩在90分以上(含90分)的学生人数约占全体参赛人数的2.28%,因此,
参赛总人数约为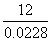 ≈526(人)。
≈526(人)。
(Ⅱ)假定设奖的分数线为x分,则
P(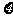 ≥x)=1-P(
≥x)=1-P(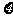 <x)=1-F(90)=1-
<x)=1-F(90)=1-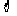
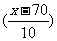 =
=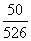 =0.0951,
=0.0951,
即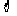
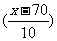 =0.9049,查表得
=0.9049,查表得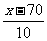 ≈1.31,解得x=83.1.
≈1.31,解得x=83.1.
故设奖得分数线约为83.1分。
(二)填空题:
4、(07全国Ⅱ)在某项测量中,测量结果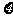 服从正态分布
服从正态分布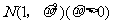 .若
.若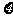 在
在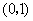 内取值的概率为0.4,则
内取值的概率为0.4,则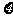 在
在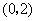 内取值的概率为
;
内取值的概率为
;
5、(05湖南)一工厂生产了某种产品16800件,它们来自甲.乙.丙3条生产线,为检查这批产品的质量,决定采用分层抽样的方法进行抽样,已知甲.乙.丙三条生产线抽取的个体数组成一个等差数列,则乙生产线生产了 件产品。
6、(04天津)某工厂生产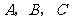 三种不同型号的产品,产品数量之比依次为
三种不同型号的产品,产品数量之比依次为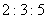 ,现用分层抽样方法抽出一个容量为
,现用分层抽样方法抽出一个容量为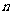 的样本,样本中
的样本,样本中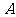 种型号产品有16件
种型号产品有16件 那么此样本的容量
那么此样本的容量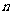 =
。
=
。
(一)选择题:
1、(07湖南)设随机变量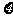 服从标准正态分布
服从标准正态分布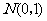 ,已知
,已知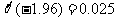 ,则
,则 =( ) A、0.025 B、0.050 C、0.950 D、0.975
=( ) A、0.025 B、0.050 C、0.950 D、0.975
2、(06重庆)为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:
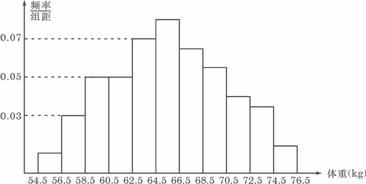
根据上图可得这100名学生中体重在(56.5,64.5)的学生人数是( )
A、20 B、30 C、40 D、50
3、(05江苏)在一次歌手大奖赛上,七位评委为歌手打出的分数如下:
9.4 8.4 9.4 9.9 9.6 9.4 9.7
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A、9.4, 0.484 B、9.4, 0.016 C、9.5, 0.04 D、9.5, 0.016
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com