
21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多作,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将选题号填入括号中.
(1)(本小题满分7分) 选修4一2:矩阵与变换
设矩阵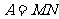 ,求矩阵
,求矩阵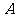 的特征值以及属于每个特征值的一个特征向量.
的特征值以及属于每个特征值的一个特征向量.
其中 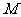 =
=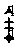
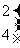 ,
,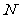 =
=
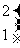
(2)(本小题满分7分) 选修4一4:坐标系与参数方程
已知直线 的参数方程:
的参数方程: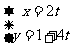 (
( 为参数),圆C的极坐标方程:
为参数),圆C的极坐标方程: ,试判断直线
,试判断直线 与圆C的位置关系.
与圆C的位置关系.
(3)(本小题满分7分) 选修4一5:不等式选讲
解不等式: .
.
2010届莆田四中高三数学(理)第一次月考
20.(本题满分14分)如图,椭圆 (a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,
(a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点, . (Ⅰ)设C是以MN为直径的圆,试判断原点O与圆C的位置关系;(Ⅱ)设椭圆的离心率为
. (Ⅰ)设C是以MN为直径的圆,试判断原点O与圆C的位置关系;(Ⅱ)设椭圆的离心率为 ,MN的最小值为
,MN的最小值为 ,求椭圆方程.
,求椭圆方程.
19.(本小题满分14分)
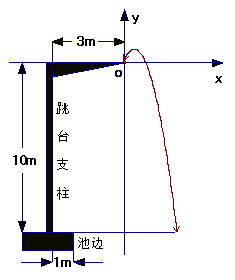
2008年北京奥运会中国跳水梦之队取得了辉煌的成绩。
据科学测算,跳水运动员进行10米跳台跳水训练时,
身体(看成一点)在空中的运动轨迹(如图所示)是
一经过坐标原点的抛物线(图中标出数字为已知条件),
且在跳某个规定动作时,正常情况下运动员在空中的最
高点距水面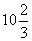 米,入水处距池边4米,同时运动员在
米,入水处距池边4米,同时运动员在
距水面5米或5米以上时,必须完成规定的翻腾动作,
并调整好入水姿势,否则就会出现失误。
(Ⅰ)求抛物线的解析式;
(Ⅱ)在某次试跳中,测得运动员在空中的运动轨迹为(1)
中的抛物线,且运动员在空中调整好入水姿势时距池边的水
平距离为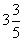 米,问此次跳水会不会失误?请通过计算说明理由;
米,问此次跳水会不会失误?请通过计算说明理由;
 (Ⅲ)某运动员按(1)中抛物线运行,要使得此次跳水成功,他在空中调整好入水姿势时,距池边的水平距离至多应为多大?
(Ⅲ)某运动员按(1)中抛物线运行,要使得此次跳水成功,他在空中调整好入水姿势时,距池边的水平距离至多应为多大?
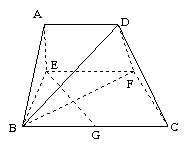
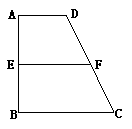
18.(本题满分13分)已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = , AB=BC=2AD=4,E、F分别是AB、CD上的点, EF∥BC, AE = x, G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).
, AB=BC=2AD=4,E、F分别是AB、CD上的点, EF∥BC, AE = x, G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).
(1)当x=2时,求证:BD⊥EG;
(2)若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
 (3)当 f(x)取得最大值时,求二面角D-BF-C的余弦值.
(3)当 f(x)取得最大值时,求二面角D-BF-C的余弦值.
17、(本题13 分)已知某个几何体的直观图,正视图和俯视图,如下,根据图中标出的尺寸 (单位:cm)
(1)画出几何体的侧视图;
(2)求这个几何体的体积;

 (3)若E、F分别是PC、AC的中点,连接EF,求EF与面PBC所成角的正弦值。
(3)若E、F分别是PC、AC的中点,连接EF,求EF与面PBC所成角的正弦值。
16.(本题满分13分)
 莆田市在每年的春节后,市政府都会发动公务员参与到植树活动中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米)
莆田市在每年的春节后,市政府都会发动公务员参与到植树活动中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米)
甲: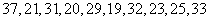
乙:
(Ⅰ)根据抽测结果,完成答题卷中的茎叶图,并根据
你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出
两个统计结论;
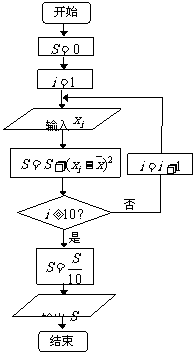
(Ⅱ)设抽测的10株甲种树苗高度平均值为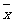 ,将
,将
这10株树苗的高度依次输入按程序框图进行的运算,问
输出的 大小为多少?并说明
大小为多少?并说明 的统计学意义。
的统计学意义。
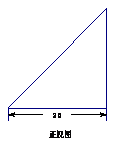
15.由图(1)有面积关系: 
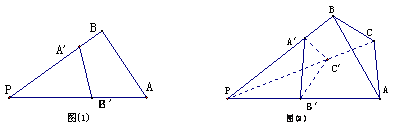 则图(2) 有体积关系:
则图(2) 有体积关系: 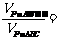 _____________ 。
_____________ 。
14.假设关于某设备使用年限x(年)和所支出的维修费用y
(万元)有如下的统计资料,若变量x与y具有线性相关关系,
用最小二乘法求其回归直线方程为
|
x |
2 |
3 |
4 |
5 |
6 |
|
y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com