
2.下列各句中,没有错别字且注音全对的一项是( )
A.三聚氰胺--种被非法加入婴幼儿配方奶粉中的化工原料,可导致人体泌(mì)尿系统产生结石,在中国已令至少6000余名婴儿致病,4名死亡。
B.国学超女于丹与学术超男易中天首次联袂(mèi)出书,同台对谈,共品人生,妙语如珠,古今交汇,将把对传统文化精典的领悟融入当下生活。
C.在北京举行的第29届奥运会上,作为东道主的中国军团,首次以51枚金牌力压美、俄跻(jī)身金牌榜之首。中国举重队和男子体操队可谓所向披糜,力挫群雄。
D.2008年诺贝尔生理学或医学奖授予德国科学家哈拉尔德?楚尔?豪森。他在上世纪70年代开始的研究中发现导至宫颈癌的HPV(人乳头状瘤病毒),使得宫颈癌成为讫(qǐ)今病因最明确的一种癌症。
答案A(B精-经 C靡-糜 D至-致 讫 qǐ-迄qì)
1.下列各组词语中,加点字的读音全都不相同的一组是(3分)
A.窥伺 伺候 俟机 恃才傲物
B.栖息 欺侮 蹊跷 误入歧途
C.擎起 亲家 罄尽 三聚氰胺
D.媲美 纰漏 癖好 蚍蜉撼树
答案 D
10. 在直三棱柱ABC-A1B1C1中,AB1⊥BC1,AB=CC1=a,BC=b.
(1)设E、F分别为AB1、BC1的中点,求证:EF∥平面ABC;
(2)求证:A1C1⊥AB;
(3)求点B1到平面ABC1的距离.

(1)证明:∵E、F分别为AB1、BC1的中点,
∴EF∥A1C1.∵A1C1∥AC,∴EF∥AC.
∴EF∥平面ABC.
(2)证明:∵AB=CC1,
∴AB=BB1.又三棱柱为直三棱柱,
∴四边形ABB1A1为正方形.连结A1B,则A1B⊥AB1.
又∵AB1⊥BC1,
∴AB1⊥平面A1BC1. ∴AB1⊥A1C1.
又A1C1⊥AA1,
∴A1C1⊥平面A1ABB1. ∴A1C1⊥AB.
(3)解:∵A1B1∥AB,∴A1B1∥平面ABC1.
∴A1到平面ABC1的距离等于B1到平面ABC1的距离.过A1作A1G⊥AC1于点G,
∵AB⊥平面ACC1A1,
∴AB⊥A1G.从而A1G⊥平面ABC1,故A1G即为所求的距离,即A1G=
 .
.
评述:本题(3)也可用等体积变换法求解.
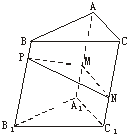
[探索题](2004年春季上海)如下图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EFcos∠DFE.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
(1)证明:∵CC1∥BB1 CC1⊥PM,CC1⊥PN,
CC1⊥PM,CC1⊥PN,
∴CC1⊥平面PMN CC1⊥MN.
CC1⊥MN.
(2)解:S2 =S2
=S2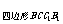 +S2
+S2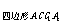 -2S
-2S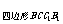 ·S
·S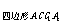 cosα,
cosα,
其中α为平面CC1B1B与平面CC1A1A所成的二面角.
∵CC1⊥平面PMN,∴上述的二面角为∠MNP.
在△PMN中,
PM2=PN2+MN2-2PN.MNcos∠MNP
 PM2CC12=PN2CC12+MN2CC12
PM2CC12=PN2CC12+MN2CC12
-2(PN·CC1)·(MN·CC1)cos∠MNP.
∵ =PN·CC1,
=PN·CC1, =MN·CC1,
=MN·CC1,
S =PM·BB1,
=PM·BB1,
∴S2 =S2
=S2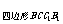 +S2
+S2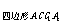 -
-
2S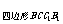 ·S
·S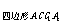 cosα
cosα
9.正方形ABCD中,AB=2,E是AB边的中点,F是BC边上一点,将△AED及△DCF折起(如下图),使A、C点重合于A′点.
(1)证明:A′D⊥EF;
(2)当F为BC的中点时,求A′D与平面DEF所成的角;
(3)当BF=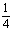 BC时,求三棱锥A′-EFD的体积.
BC时,求三棱锥A′-EFD的体积.

(1)证明:略
(2)解:取EF的中点G,连结A′G、DG…………
平面DEF⊥平面A′DG.
作A′H⊥DG于H,得A′H⊥平面DEF,
∴∠A′DG为A′D与平面DEF所成的角.
在Rt△A′DG中,A′G= ,
,
A′D=2, ∴∠A′DG=arctan .
.

(3)解:∵A′D⊥平面A′EF,
∴A′D是三棱锥D-A′EF的高.
又由BE=1,BF=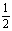 推出EF=
推出EF= ,可得S
,可得S =
= ,
,
VA′-EFD=VD-A′EF= ·S
·S ·A′D
·A′D
= ·
· ·2=
·2=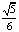 .
.
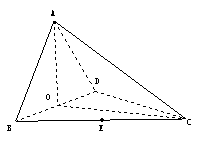
8.(2006福建) 如图,四面体ABCD中,O、E分别是BD、BC的中点,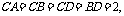

(I)求证: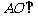 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
 (III)求点E到平面ACD的距离.
(III)求点E到平面ACD的距离.
解法一:
(I)证明:证∠AOB=900.
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知
 直线OE与EM所成的锐角就是异面直线AB与CD所成的角. 在
直线OE与EM所成的锐角就是异面直线AB与CD所成的角. 在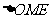 中,
中,

 是直角
是直角 斜边AC上的中线,
斜边AC上的中线,
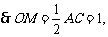

AB与CD所成角的大小为
(III)等积法得


即为所求.
7.如图ABCD是矩形,PA^平面ABCD,DPAD是等腰三角形,M、N分别是AB、PC的中点,求证:MN^平面PCD
 证略
证略
6. AC⊥BD或四边形ABCD菱形等;
[解答题]
6.
在直四棱柱ABCD-A1B1C1D1中,当底面四边形ABCD满足条件_______时,有A1C⊥B1D1 (注:填上你认为正确的一种条件即可,不必考虑所有可能的情况)
(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况)
◆答案提示: 1-4 CDAC; 5.3cm;
5.△ABC的三个顶点A、B、C到平面α的距离分别为2 cm、3 cm、4 cm,且它们在α的同侧,则△ABC的重心到平面α的距离为______
4.PA垂直于以AB为直径的圆所在的平面,C为圆上异于A、B的任一点,则下列关系不正确的是 ( )
A PA⊥BC B BC⊥平面PAC C AC⊥PB D PC⊥BC
[填空题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com