
22.(14分)
解:(Ⅰ)将点 代入
代入 中得
中得
 …………………………………………(4分)
…………………………………………(4分)
(Ⅱ) ………………………………(5分)
………………………………(5分)
 ……………………(8分)
……………………(8分)
(Ⅲ)由

………………………………(14分)
22.(14分)已知正项数列 中,
中,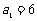 ,点
,点 在抛物线
在抛物线 上;数列
上;数列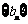 中,点
中,点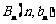 在过点
在过点 ,以方向向量为
,以方向向量为 的直线上。
的直线上。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,问是否存在
,问是否存在 ,使
,使 成立,若存在,求出
成立,若存在,求出 值;若不存在,说明理由;
值;若不存在,说明理由;
(Ⅲ)对任意正整数 ,不等式
,不等式 成立,求正数
成立,求正数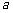 的取值范围。
的取值范围。
21.(12分)已知抛物线、椭圆和双曲线都经过点 ,它们在
,它们在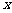 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。
轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。
(Ⅰ)求这三条曲线的方程;
(Ⅱ)已知动直线 过点
过点 ,交抛物线于
,交抛物线于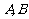 两点,是否存在垂直于
两点,是否存在垂直于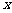 轴的直线
轴的直线 被以
被以 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
21 (12分)
(12分)
解:(Ⅰ)设抛物线方程为 ,将
,将 代入方程得
代入方程得
 ………………………………………………(1分)
………………………………………………(1分)
由题意知椭圆、双曲线的焦点为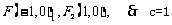 …………………(2分)
…………………(2分)
对于椭圆,
 ………………………………(4分)
………………………………(4分)
对于双曲线,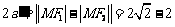
 ………………………………(6分)
………………………………(6分)
(Ⅱ)设 的中点为
的中点为 ,
, 的方程为:
的方程为: ,以
,以 为直径的圆交
为直径的圆交 于
于 两点,
两点,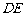 中点为
中点为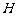
令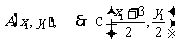 ………………………………………………(7分)
………………………………………………(7分)

 …………(12分)
…………(12分)
1.重庆一模
17]两个单摆摆长相同,一个静止于地面,一个个静止在悬浮于高空的气球中。地面上的单摆摆动了n次全振动时,气球中的单摆摆动了n-1次全振动。已知地球半径为R,求气球的高度?
 [18]图7-5-1所示为一单摆的共振曲线,则该单摆的摆长约为多少?共振时单摆的振幅是多大?共振时单摆的最大速度和最大加速度各是多大?(g取10m/s2)
[18]图7-5-1所示为一单摆的共振曲线,则该单摆的摆长约为多少?共振时单摆的振幅是多大?共振时单摆的最大速度和最大加速度各是多大?(g取10m/s2)




 [19]如图7-5-2所示,两东西向放置的相干声源S1和S2相距25m,在S1和S2中垂线上正北方距离S1和S2连线12m处有一点A,某人站在A处听到声音很响,此人自A向正西方走,听到声音逐渐减弱,走到距离A3.5m的B处,完全听不到声音,求声波的波长。
[19]如图7-5-2所示,两东西向放置的相干声源S1和S2相距25m,在S1和S2中垂线上正北方距离S1和S2连线12m处有一点A,某人站在A处听到声音很响,此人自A向正西方走,听到声音逐渐减弱,走到距离A3.5m的B处,完全听不到声音,求声波的波长。


 [20]如图7-5-3所示,虚线和实线分别为一列简谐横波上两质点P、Q的振动图象,两质点相距30m,则
[20]如图7-5-3所示,虚线和实线分别为一列简谐横波上两质点P、Q的振动图象,两质点相距30m,则
⑴若P质点离波源近,则波速多大?
⑵若Q质点离波源近,则波速多大?
 [21]如图7-5-4所示,有一长度为S=1.6m的水平轨道AB,在B点处与半径为250m的光滑弧形轨道BC相切,A处为一竖直墙壁。一质量为0.99kg的木块静止于B处,现有一质量为10g的子弹以500m/s的水平速度从左边射入木块且未穿出。已知木块与该水平轨道间的动摩擦因数μ=0.1,木块与墙壁的碰撞无机械能损失,g取10m/s2,求:子弹射入木块后,木块需经多长时间才能停下来?
[21]如图7-5-4所示,有一长度为S=1.6m的水平轨道AB,在B点处与半径为250m的光滑弧形轨道BC相切,A处为一竖直墙壁。一质量为0.99kg的木块静止于B处,现有一质量为10g的子弹以500m/s的水平速度从左边射入木块且未穿出。已知木块与该水平轨道间的动摩擦因数μ=0.1,木块与墙壁的碰撞无机械能损失,g取10m/s2,求:子弹射入木块后,木块需经多长时间才能停下来?


10]一物体在某行星表面受到的万有引力是它在地球表面所受万有引力的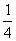 .在地球上走时准确的机械摆钟移到此行星表面上后,摆钟的分针走一圈所用的时间为地球时间( )
.在地球上走时准确的机械摆钟移到此行星表面上后,摆钟的分针走一圈所用的时间为地球时间( )
A、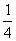 h B、
h B、 h C、2h D、4h
h C、2h D、4h
 [11]在水平方向做简谐运动的弹簧振子,其质量为m,最大速率为v,则下列说法正确的是( )
[11]在水平方向做简谐运动的弹簧振子,其质量为m,最大速率为v,则下列说法正确的是( )
A、从某时刻起,在半个周期时间内,弹力做功一定为零
B、从某时刻起,在半个周期时间内,弹力做的功可能是0到 mv2之间的某一个值
mv2之间的某一个值
C、从某时刻起,在半个周期时间内,弹力的冲量一定为零
D、从某时刻起,在半个周期时间内,弹力的冲量可能是0到2mv之间的某一个值
 [12]如图7-3-1所示,沿波的传播方向上有间距为1m的六个质点a、b、c、d、e、f,均静止在各自的平衡位置。一列横波以1m/s的速度向右传播,t=0时刻到达a质点,质点a开始由平衡位置向上运动。t=1s时,质点a第一次到达最高点,则在4s<t<5s这段时间内( )
[12]如图7-3-1所示,沿波的传播方向上有间距为1m的六个质点a、b、c、d、e、f,均静止在各自的平衡位置。一列横波以1m/s的速度向右传播,t=0时刻到达a质点,质点a开始由平衡位置向上运动。t=1s时,质点a第一次到达最高点,则在4s<t<5s这段时间内( )
A、质点c的加速度逐渐增大
B、质点a的速度逐渐增大
 C、指点d向下运动
C、指点d向下运动
D、质点f保持静止
 [13]两列相干波的振幅分别为A1和A2,某时刻介质中质点P的位移大小为A1+A2,则( )
[13]两列相干波的振幅分别为A1和A2,某时刻介质中质点P的位移大小为A1+A2,则( )
A、质点的振幅一直为A1+A2
B、质点的振幅再过半个周期为∣A1-A2∣
C、质点的位移大小一直为A1+A2
D、质点的位移大小再过半个周期为A1+A2


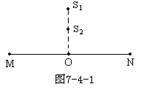 [14]如图7-4-1所示,S1和S2是湖面上两个完全相同的水波的波源,MN是足够长的湖岸,水波的波长为2m,S1与S2的连线与湖岸垂直,且S1S2=5m,则岸边始终平静的地方共有( )
[14]如图7-4-1所示,S1和S2是湖面上两个完全相同的水波的波源,MN是足够长的湖岸,水波的波长为2m,S1与S2的连线与湖岸垂直,且S1S2=5m,则岸边始终平静的地方共有( )



A、1处 B、3处 C、5处 D、无数处



 [15]图7-4-2是观察水面波衍射的实验装置,AC和BD是两块挡板,AB是一个孔,O是波源。图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)间的距离表示一个波长,则波经过孔之后的传播情况,下列说法中正确的是( )
[15]图7-4-2是观察水面波衍射的实验装置,AC和BD是两块挡板,AB是一个孔,O是波源。图中已画出波源所在区域波的传播情况,每两条相邻波纹(图中曲线)间的距离表示一个波长,则波经过孔之后的传播情况,下列说法中正确的是( )





A、此时能明显观察到波的衍射现象
B、挡板前后波纹间距离相等
C、如果将孔AB扩大,有可能观察不到明显的衍射现象
D、如果孔的大小不变,将波源的频率增大,将能更明显地观察到衍射现象
 [16]如图7-4-3所示,向左匀速运动的小车发出频率为f的声波,车左侧A处的人感受到的声波的频率为f1,车右侧B处的人感受到的声波的频率为f2,则( )
[16]如图7-4-3所示,向左匀速运动的小车发出频率为f的声波,车左侧A处的人感受到的声波的频率为f1,车右侧B处的人感受到的声波的频率为f2,则( )
A、f1<f,f2<f B、f1<f,f2>f C、f1>f,f2>f D、f1>f,f2<f






[答案]D 
[解析]由于波源向A相对靠近,所以f1<f;而波源相对B远离,所以f2<f。
[易错点点睛]掌握多普勒效应的规律。
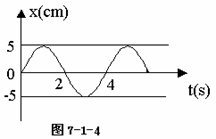
8]图7-1-4所示为一沿水平方向振动的弹簧振子的振动图象,求⑴从计时开始,什么时刻第一次达到弹性势能最大?⑵在第2s末到第3s末这段时间内振子的加速度、速度、动能、弹性势能各怎么变化?⑶该振子在前100s内总位移是多少?总路程是多少?






 [9]单摆做简谐运动时,下列说法正确的是( )
[9]单摆做简谐运动时,下列说法正确的是( )
A、摆球质量越大、振幅越大,则单摆振动的能量越大
B、单摆振动能量与摆球质量无关,与振幅有关
C、摆球到达最高点时势能最大,摆线弹力最大
D、摆球通过平衡位置时动能最大,摆线弹力最大


4]如图所示表示两列相干水波的叠加情况,图中的实线表示波峰,虚线表示波谷。设两列波的振幅均为5 cm,且图示的范围内振幅不变,波速和波长分别为1m/s和0.5m。C点是BE连线的中点,下列说法中正确的是 (
)
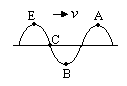 A.C、E两点都保持静止不动
A.C、E两点都保持静止不动
B.图示时刻A、B两点的竖直高度差为20cm
C.图示时刻C点正处于平衡位置且向水面上运动
D.从图示的时刻起经0.25s,B点通过的路程为20cm
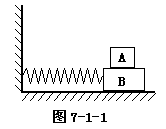
 [5] 如图7-1-1所示,质量为m的物体A放在质量为M的物体B上,B与弹簧相连,它们一起在光滑水平面上做简谐运动,振动过程中A、B之间无相对运动。设弹簧劲度系数为k,但物体离开平衡位置的位移为x时,A、B间摩擦力的大小等于( )
[5] 如图7-1-1所示,质量为m的物体A放在质量为M的物体B上,B与弹簧相连,它们一起在光滑水平面上做简谐运动,振动过程中A、B之间无相对运动。设弹簧劲度系数为k,但物体离开平衡位置的位移为x时,A、B间摩擦力的大小等于( )
 A、kx B、
A、kx B、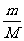

C、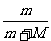 kx
D、0
kx
D、0

 [6]一弹簧振子做简谐运动,周期为T,则正确的说法是( )
[6]一弹簧振子做简谐运动,周期为T,则正确的说法是( )
A、若t时刻和(t+Δt)时刻振子运动位移的大小相等、方向相同,则Δt一定等于T的整数倍
B、若t时刻和(t+Δt)时刻振子运动速度的大小相等、方向相同,则Δt一定等于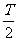 的整数倍
的整数倍
C、若Δt=T,则在t时刻和(t+Δt)时刻振子运动的加速度一定相等
D、若Δt=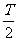 ,则在t时刻和(t+Δt)时刻弹簧的长度一定相等
,则在t时刻和(t+Δt)时刻弹簧的长度一定相等


 [7]如图7-1-3所示,一质点在平衡位置o点两侧做简谐运动,在它从平衡位置出发,向端点A处运动过程中,经0.15s第一次经过M点,在经0.1s第二次经过M点,则该质点的振动频率为( )
[7]如图7-1-3所示,一质点在平衡位置o点两侧做简谐运动,在它从平衡位置出发,向端点A处运动过程中,经0.15s第一次经过M点,在经0.1s第二次经过M点,则该质点的振动频率为( )
A、0.8Hz B、1Hz C、1.25Hz D、1.5Hz
[答案] C
[解析] O到M用时0.15s,M到A再回到M用时0.1s,根据对称性,M到A用时为0.05s,所以O到A用时为0.2s,因此周期为0.8s,而频率为1.25Hz.所以C选项正确。
[易错点点睛]简谐运动的对称性包括状态的对称性和过程的对称性,这题就是利用了M到A和从A回到M的等时对称性
3]如图所示,S1、S2是两个相干波源,它们振动同步且振幅相同。实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷。关于图中所标的a、b、c、d四点,下列说法中正确的有
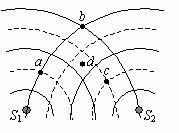

A.该时刻a质点振动最弱,b、c质点振动最强,d质点振动既不是最强也不是最弱 
B.该时刻a质点振动最弱,b、c、d质点振动都最强
C.a质点的振动始终是最弱的, b、c、d质点的振动始终是最强的
D.再过T/4后的时刻a、b、c三个质点都将处于各自的平衡位置,因此振动最弱
 [易错点点睛]描述振动强弱的物理量是振幅,而振幅不是位移。每个质点在振动过程中的位移是在不断改变的,但振幅是保持不变的,所以振动最强的点无论处于波峰还是波谷,振动始终是最强的。
[易错点点睛]描述振动强弱的物理量是振幅,而振幅不是位移。每个质点在振动过程中的位移是在不断改变的,但振幅是保持不变的,所以振动最强的点无论处于波峰还是波谷,振动始终是最强的。
1]一个弹簧振子,第一次被压缩x后释放做自由振动,周期为T1,第二次被压缩2x后释放做自由振动,周期为T2,则两次振动周期之比T1∶T2为 
A.1∶1
B.1∶2
C.2∶1
C.1∶4
 [2]一个单摆,如果摆球的质量增加为原来的4倍,摆球经过平
[2]一个单摆,如果摆球的质量增加为原来的4倍,摆球经过平


A.频率不变,振幅不变
B.频率不变,振幅改变
C.频率改变,振幅不变
D.频率改变,振幅改变


单摆的周期与质量无关,与单摆的运动速度也无关。当然,频率也与质量和速度无关,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com