
3.下列反应属于非氧化还原反应的是( )
A.Fe2O3+3CO 2Fe+3CO2
2Fe+3CO2
B.NH4NO3 N2O↑十2H2O
N2O↑十2H2O
C.2NaHCO3 Na2CO3+CO2↑十H2O
Na2CO3+CO2↑十H2O
D.Cu2(OH)2CO3 2CuO+CO2↑+H2O
2CuO+CO2↑+H2O
2.下列反应不一定是氧化还原反应的是( )
A.化合反应 B.分解反应 C.复分解反应 D.置换反应
1.氧化还原反应的实质是( )
A.元素化合价发生变化
B.反应中有氧原子的得失
C.反应中有电子得失或电子对的偏移
D.反应后生成新物质
14、已知二次函数 同时满足:①不等式
同时满足:①不等式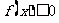 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在 ,使得不等式
,使得不等式 成立。
成立。
设数列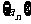 的前
的前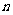 项和
项和 ,
,
(1)求数列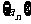 的通项公式;
的通项公式;
(2)试构造一个数列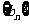 ,(写出
,(写出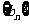 的一个通项公式)满足:对任意的正整数
的一个通项公式)满足:对任意的正整数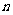 都有
都有 ,且
,且 ,并说明理由;
,并说明理由;
(3)设各项均不为零的数列 中,所有满足
中,所有满足 的正整数
的正整数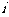 的个数称为这个数列
的个数称为这个数列 的变号数。令
的变号数。令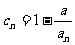 (
(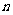 为正整数),求数列
为正整数),求数列 的变号数。
的变号数。
解:(1)∵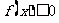 的解集有且只有一个元素,∴
的解集有且只有一个元素,∴ ,
,
当 时,函数
时,函数 在
在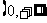 上递增,故不存在
上递增,故不存在 ,使得不等式
,使得不等式 成立。
成立。
当 时,函数
时,函数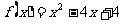 在
在 上递减,故存在
上递减,故存在 ,使得不等式
,使得不等式 成立。
成立。
综上,得 ,
,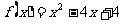 ,∴
,∴ ,
,

∴
(2)要使 ,可构造数列
,可构造数列 ,∵对任意的正整数
,∵对任意的正整数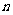 都有
都有 ,
,
∴当 时,
时,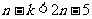 恒成立,即
恒成立,即 恒成立,即
恒成立,即 ,
,
又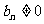 ,∴
,∴ ,∴
,∴ ,等等。
,等等。
(3)解法一:由题设 ,
,
∵ 时,
时,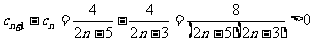 ,
,
∴ 时,数列
时,数列 递增,
递增,
∵ ,由
,由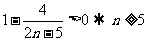 ,
,
可知 ,即
,即 时,有且只有
时,有且只有 个变号数;
个变号数;
又∵ ,即
,即 ,
,
∴此处变号数有 个。
个。
综上得
数列 共有
共有 个变号数,即变号数为
个变号数,即变号数为 。
。
解法二:由题设 ,
,
 时,令
时,令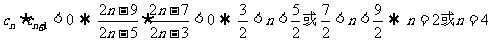 ;
;
又∵ ,∴
,∴ 时也有
时也有 。
。
综上得 数列 共有
共有 个变号数,即变号数为
个变号数,即变号数为 。
。
13、已知等比数列{an}的前n项和为Sn.
(Ⅰ)若Sm,Sm+2,Sm+1成等差数列,证明am,am+2,am+1成等差数列;
(Ⅱ)写出(Ⅰ)的逆命题,判断它的真伪,并给出证明.
证:(Ⅰ) ∵Sm+1=Sm+am+1,Sm+2=Sm+am+1+am+2.
由已知2Sm+2=Sm+Sm+1,∴ 2(Sm+am+1+am+2)=Sm+(Sm+am+1),
∴am+2=-am+1,即数列{an}的公比q=-.
∴am+1=-am,am+2=am,∴2am+2=am+am+1,∴am,am+2,am+1成等差数列.
(Ⅱ) (Ⅰ)的逆命题是:若am,am+2,am+1成等差数列,则Sm,Sm+2,Sm+1成等差数列.
设数列{an}的公比为q,∵am+1=amq,am+2=amq2.
由题设,2am+2=am+am+1,即2amq2=am+amq,即2q2-q-1=0,∴q=1或q=-.
当q=1时,A≠0,∴Sm, Sm+2, Sm+1不成等差数列.
逆命题为假.
12、(Ⅰ)已知函数: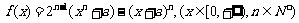 求函数
求函数 的最小值;
的最小值;
(Ⅱ)证明: ;
;
(Ⅲ)定理:若 均为正数,则有
均为正数,则有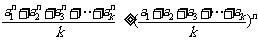 成立
成立
(其中 .请你构造一个函数
.请你构造一个函数 ,证明:
,证明:
当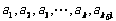 均为正数时,
均为正数时, .
.
解:(Ⅰ)令 得
得 …2分
…2分
当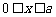 时,
时,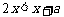
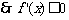 故
故 在
在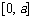 上递减.
上递减.
当 故
故 在
在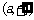 上递增.所以,当
上递增.所以,当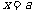 时,
时, 的最小值为
的最小值为 .….4分
.….4分
(Ⅱ)由 ,有
,有 即
即
故  .………………………………………5分
.………………………………………5分
(Ⅲ)证明:要证: 
只要证:
设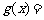
 …………………7分
…………………7分
则
令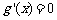 得
得 …………………………………………………….8分
…………………………………………………….8分
当
 时,
时,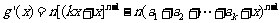


故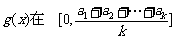 上递减,类似地可证
上递减,类似地可证 递增
递增
所以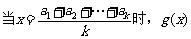 的最小值为
的最小值为 ………………10分
………………10分
而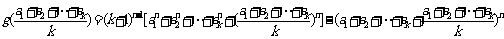
=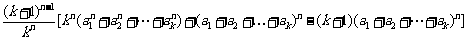
= =
=
由定理知:  故
故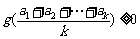

故
即:  .…………………………..14分
.…………………………..14分
11、已知函数y=f(x)满足f(a-tanθ)=cotθ-1,(其中,a、θ∈R均为常数)
(1)求函数y=f(x)的解析式;
(2)利用函数y=f(x)构造一个数列{xn},方法如下:
对于给定的定义域中的x1,令x2= f(x1),x3= f(x2),…,xn= f(xn-1),…
在上述构造过程中,如果xi(i=1,2,3,…)在定义域中,构造数列的过程继续下去;如果xi不在定义域中,则构造数列的过程停止.
① 如果可以用上述方法构造出一个常数列{xn},求a的取值范围;
② 如果取定义域中的任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求a实数的值.
 解:(1)令
解:(1)令 则
则

①×②,并整理,得 y= ,
,
∴y=f(x) = , (x≠a). ………………………………4分
, (x≠a). ………………………………4分
(2)①根据题意,只需当x≠a时,方程f(x) =x有解,
亦即方程 x2+(1-a)x+1-a=0 有不等于的解.
将x=a代入方程左边,得左边为1,故方程不可能有解x=a.
由 △=(1-a)2-4(1-a)≥0,得 a≤-3或a≥1,
即实数a的取值范围是 . …………………………9分
. …………………………9分
②根据题意, =a在R中无解,
=a在R中无解,
亦即当x≠a时,方程(1+a)x=a2+a-1无实数解.
由于x=a不是方程(1+a)x=a2+a-1的解,
所以对于任意x∈R,方程(1+a)x=a2+a-1无实数解,
∴ a= -1即为所求a的值. ……………………………………14分
10、
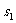 ,
, ,┅,
,┅,
 ,
,
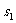 ,
, ,┅,
,┅,
 分别表示实数
分别表示实数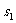 ,
, ,┅,
,┅, 中的最小者和最大者.
中的最小者和最大者.
(1)作出函数 =|
=| +3|+2|
+3|+2| -1|(
-1|( ∈R)的图像;
∈R)的图像;
(2)在求函数 =|
=| +3|+2|
+3|+2| -1|(
-1|( ∈R)的最小值时,有如下结论:
∈R)的最小值时,有如下结论:
 =
=
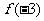 ,
,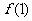
 =4.请说明此结论成立的理由;
=4.请说明此结论成立的理由;
(3)仿照(2)中的结论,讨论当 ,
, ,┅,
,┅,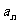 为实数时,
为实数时,
函数 =
= +
+ +┅+
+┅+

 ∈R,
∈R,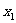 <
< <┅<
<┅< ∈R
∈R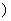 的最值.
的最值.
解:(1)图略;
(2)当 ∈(-∞,-3)时,
∈(-∞,-3)时, 是减函数,
是减函数,
当 ∈
∈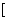 -3,1)时,
-3,1)时, 是减函数,
是减函数,
当 ∈
∈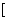 1,+∞)时,
1,+∞)时, 是增函数,
是增函数,
∴ =
=
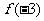 ,
,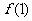
 =4.
=4.
(3)当 +
+ +┅+
+┅+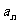 <0时,
<0时, =
=
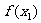 ,
,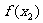 ,┅,
,┅,
 ;
;
当 +
+ +┅+
+┅+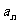 >0时,
>0时, =
=
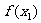 ,
,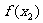 ,┅,
,┅,
 ;
;
当 +
+ +┅+
+┅+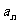 =0时,
=0时, =
=
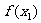 ,
,
 ,
,
 =
=
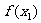 ,
,
 .
.
9、对于在区间[m,n]上有意义的两个函数f (x)与g (x),如果对任意x∈[m,n]均有| f
(x) – g (x) |≤1,则称f (x)与g (x)在[m,n]上是接近的,否则称f (x)与g (x)在[m,n]上是非接近的,现有两个函数f 1(x)
= loga(x – 3a)与f 2 (x)
= loga (a > 0,a≠1),给定区间[a + 2,a + 3]
(a > 0,a≠1),给定区间[a + 2,a + 3] 
(1)若f 1(x)与f 2 (x)在给定区间[a + 2,a + 3]上都有意义,求a的取值范围;
(2)讨论f 1(x)与f 2 (x)在给定区间[a + 2,a + 3]上是否是接近的?
解:(1)要使f 1 (x)与f 2 (x)有意义,则有

要使f 1 (x)与f 2 (x)在给定区间[a + 2,a + 3]上有意义,
等价于真数的最小值大于0
 即
即
(2)f 1 (x)与f 2 (x)在给定区间[a + 2,a + 3]上是接近的
 | f 1 (x) – f 2 (x)|≤1
| f 1 (x) – f 2 (x)|≤1

 ≤1
≤1
 |loga[(x – 3a)(x – a)]|≤1
|loga[(x – 3a)(x – a)]|≤1
 a≤(x – 2a)2 – a2≤
a≤(x – 2a)2 – a2≤
对于任意x∈[a + 2,a + 3]恒成立
设h(x) = (x – 2a)2 – a2,x∈[a + 2,a + 3]
 且其对称轴x = 2a < 2在区间[a
+ 2,a + 3]的左边
且其对称轴x = 2a < 2在区间[a
+ 2,a + 3]的左边




当 时
时
f 1 (x)与f 2 (x)在给定区间[a + 2,a + 3]上是接近的
当 < a < 1时,f 1 (x)与f 2
(x)在给定区间[a + 2,a + 3]上是非接近的.
< a < 1时,f 1 (x)与f 2
(x)在给定区间[a + 2,a + 3]上是非接近的.
8、已知函数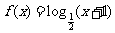 ,当点
,当点 在
在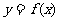 的图像上移动时,
的图像上移动时,
点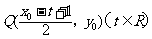 在函数
在函数 的图像上移动.
的图像上移动.
(1) 若点P坐标为(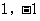 ),点Q也在
),点Q也在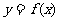 的图像上,求
的图像上,求 的值;
的值;
(2) 求函数 的解析式;
的解析式;
(3) 当 时,试探求一个函数
时,试探求一个函数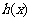 使得
使得 在限定定义域为
在限定定义域为
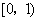 时有最小值而没有最大值.
时有最小值而没有最大值.
解:(1)当点 坐标为(
坐标为(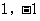 ),点
),点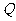 的坐标为
的坐标为 ,…………2分
∵点
,…………2分
∵点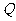 也在
也在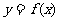 的图像上,∴
的图像上,∴ ,即
,即 .……5分
.……5分
(根据函数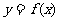 的单调性求得
的单调性求得 ,请相应给分)
(2)设
,请相应给分)
(2)设 在
在 的图像上
则
的图像上
则 ,即
,即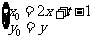 ……………………………………8分
而
……………………………………8分
而 在
在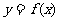 的图像上,∴
的图像上,∴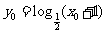 代入得,
代入得,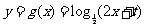 为所求.…………………………………11分
为所求.…………………………………11分
(3)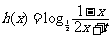 ;或
;或 等. …………………15分
如:当
等. …………………15分
如:当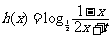 时,
时,


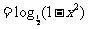
∵ 在
在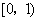 单调递减, ∴
单调递减, ∴ 故
故  ,
即
,
即 有最小值
有最小值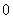 ,但没有最大值.………………………18分
,但没有最大值.………………………18分
(其他答案请相应给分)
(参考思路)在探求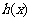 时,要考虑以下因素:①
时,要考虑以下因素:①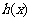 在
在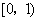 上必须有意义(否则不能参加与
上必须有意义(否则不能参加与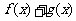 的和运算);②由于
的和运算);②由于 和
和 都是以
都是以 为底的对数,所以构造的函数
为底的对数,所以构造的函数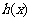 可以是以
可以是以 为底的对数,这样与
为底的对数,这样与 和
和 进行的运算转化为真数的乘积运算;③以
进行的运算转化为真数的乘积运算;③以 为底的对数是减函数,只有当真数取到最大值时,对数值才能取到最小值;④为方便起见,可以考虑通过乘积消去
为底的对数是减函数,只有当真数取到最大值时,对数值才能取到最小值;④为方便起见,可以考虑通过乘积消去 ;⑤乘积的结果可以是
;⑤乘积的结果可以是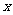 的二次函数,该二次函数的图像的对称轴应在直线
的二次函数,该二次函数的图像的对称轴应在直线 的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与
的左侧(否则真数会有最小值,对数就有最大值了),考虑到该二次函数的图像与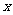 轴已有了一个公共点
轴已有了一个公共点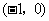 ,故对称轴又应该是
,故对称轴又应该是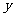 轴或在
轴或在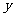 轴的右侧(否则该二次函数的值在
轴的右侧(否则该二次函数的值在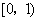 上的值不能恒为正数),即若抛物线与
上的值不能恒为正数),即若抛物线与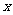 轴的另一个公共点是
轴的另一个公共点是 ,则
,则 ,且抛物线开口向下.
,且抛物线开口向下.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com