
1.(杭州第十中学2008学年高三月考)下列晶体中不属于原子晶体的是
A.干冰 B.金刚砂 C.金刚石 D.水晶
22.
设 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,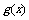 的图象与
的图象与 的图象关于直
的图象关于直
线 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时, 222233.
222233.
(1)求 的解析式;
的解析式;
(2)若 在
在 上为增函数,求
上为增函数,求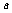 的取值范围;
的取值范围;
(3)是否存在正整数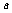 ,使
,使 的图象的最高点落在直线
的图象的最高点落在直线 上?若存在,求出
上?若存在,求出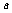 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解:(1)当x∈[-1,0]时,2-x∈[2,3],f(x)=g(2-x)= -2ax+4x3;当x∈ 时,f(x)=f(-x)=2ax-4x3,∴
时,f(x)=f(-x)=2ax-4x3,∴
(2)由题设知,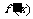 >0对x∈
>0对x∈ 恒成立,即2a-12x2>0对x∈
恒成立,即2a-12x2>0对x∈ 恒成立,于是,a>6x2,从而a>(6x2)max=6
恒成立,于是,a>6x2,从而a>(6x2)max=6
(3)因f(x)为偶函数,故只需研究函数f(x)=2ax-4x3在x∈ 的最大值.
的最大值.
令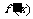 =2a-12x2=0,得
=2a-12x2=0,得 .若
.若 ∈
∈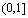 ,即0<a≤6,则
,即0<a≤6,则
 ,
,
故此时不存在符合题意的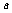 ;21世纪教育网
;21世纪教育网
若 >1,即a>6,则
>1,即a>6,则 在
在 上为增函数,于是
上为增函数,于是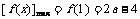 .
.
令2a-4=12,故a=8. 综上,存在a = 8满足题设.
21.解法(一):(1)设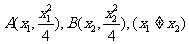
由 得:
得: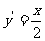

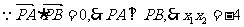
直线PA的方程是: 即
即 ①
①
同理,直线PB的方程是: ②21世纪教育网
②21世纪教育网
由①②得:
∴点P的轨迹方程是
(2)由(1)得:
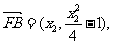


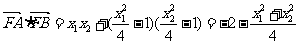

所以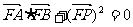
故存在 =1使得
=1使得
解法(二):(1)∵直线PA、PB与抛物线相切,且
∴直线PA、PB的斜率均存在且不为0,且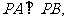
设PA的直线方程是
由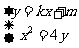 得:
得:
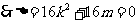 即
即
即直线PA的方程是: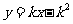 21世纪教育网
21世纪教育网
同理可得直线PB的方程是:
由 得:
得:
故点P的轨迹方程是
(2)由(1)得: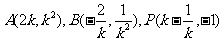

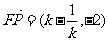

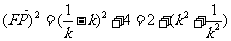 21世纪教育网
21世纪教育网
故存在 =1使得
=1使得
21.过抛物线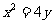 上不同两点A、B分别作抛物线的切线相交于P点,
上不同两点A、B分别作抛物线的切线相交于P点, (1)求点P的轨迹方程;
(1)求点P的轨迹方程;
(2)已知点F(0,1),是否存在实数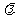 使得
使得 ?若存在,求出
?若存在,求出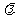 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
20. 已知点Pn(an,bn)都在直线L:y=2x+2上,P1为直线L与x轴的交点,数列{an}成等差数列,公差为1(n∈N*)。
(1)求数列{an},{bn}的通项公式;
(2)若f(n)= ,问是否存在k∈N*,使得f(k+5)=2f(k)-2成立?若存在,求出k的值,若不存在,说明理由;
,问是否存在k∈N*,使得f(k+5)=2f(k)-2成立?若存在,求出k的值,若不存在,说明理由;
20解:(1)P1(-1,0),an=-1+(n-1)×1=n-2,bn=2(n-2)+2=2n-2 21世纪教育网
(2)f(n)= ,假设存在符合条件的k
,假设存在符合条件的k
①若k为偶数,则k+5为奇数,有f(k+5)=k+3,f(k)=2k-2,如果f(k+5)=2f(k)-2,则k+3=4k-6 k=3与k为偶数矛盾。
k=3与k为偶数矛盾。
②若k为奇数,则k+5为偶数,有f(k+5)=2k+8,f(k)=k-2,如果f(k+5)=2f(k)-2,则2k+8=2k-6,这样的k也不存在。 故不存在符合条件的k
19.(1)证明:∵正四棱柱ABCD-A1B1C1D1; ∴PC⊥面ABCD,
∴P在ABCD上射影为C
又∵BD⊥AC ∴AP⊥BD
(2)解:延长BC,B1P,交于点R,过B作BQ⊥AR于Q,连结B1Q
∴B1在面ABCD上射影为C ; BQ⊥AR,AR 面ABCD; ∴B1Q⊥AR
面ABCD; ∴B1Q⊥AR
∴∠B1QB为二面角B1-AR-B的平面角 .设P底边长为G,则BQ=
tan∠B1QB=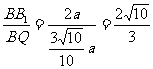 , cos∠B1QB=
, cos∠B1QB= ; 21世纪教育网
; 21世纪教育网
19.在正四棱柱ABCD-A1B1C1D1中,侧棱长是底面边长的2倍,P是侧棱CC1上的任意一动点 .(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
 (2)(理)若CC1=3C1P,求平面AB1P与平面ABCD所成的二面角的余弦值;
(2)(理)若CC1=3C1P,求平面AB1P与平面ABCD所成的二面角的余弦值;
(文)若CC1=2C1P,求二面角A–BP–B的大小;
18、某实验室新购进10件精密仪器,因运输途中一次意外紧急刹车,导致其中3件仪器有不同程度的破损(变成废品),余下7件完好无损。现从包装箱中一件一件地抽取仪器,假设每件仪器抽到的可能性都相同.
(1)若每次抽出后都不放回,当拿到完好无损仪器时停止抽取,请写出抽取次数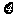 的概率分布律(只列表,不要求计算过程).
的概率分布律(只列表,不要求计算过程).
(2)求 .
.
解 (1)
由题可知,随机变量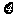 的概率分布律为:
的概率分布律为:
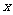 |
1 |
2 |
3 |
4 |
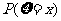 |
 |
 |
 |
 |
(2) 由(1)可知,
=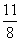 .
.
17.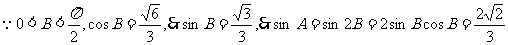 ,
,
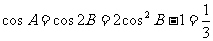
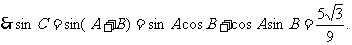 21世纪教育网
21世纪教育网
(2)在△ACD中,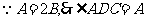 ,由正弦定理得,
,由正弦定理得,

17.已知 中,角A、B、C对应的边为a、b、c,
中,角A、B、C对应的边为a、b、c,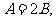
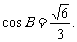
(1)求 的值;
的值;
(2)若角A的内角平分线AD的长为2,求b的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com