
3.如图是将二进制数11111(2)化为十进制数的一个程序框图,判断框内应填入的条件是( )
A.i≤5 B.i≤4
C.i>5 D.i>4
2.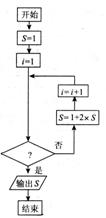 A =
A = “x∈A”是“x∈B”的( )
“x∈A”是“x∈B”的( )
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分也非必要条件
1.设U为全集,M、P是U的两个非空子集,且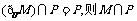 等于( )
等于( )
A.M B.P C. D.
D.
19.(本小题满分13分)
已知数列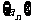 的前
的前 项和为
项和为 ,对任意
,对任意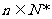 ,点
,点 都在函数
都在函数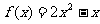 的图像上.
的图像上.
(1)求数列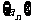 的通项公式;
的通项公式;
(2)设 ,且数列
,且数列 是等差数列,求非零常数
是等差数列,求非零常数 的值;
的值;
(3)设 ,
, 是数列
是数列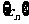 的前
的前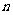 项和,求使得
项和,求使得 对所有
对所有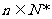 都成立的最小正整数
都成立的最小正整数 .
.
解析:(1)由已知,对所有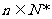 ,
, ,
……(1分)
,
……(1分)
所以当 时,
时, ,
,
当 时,
时, ,
,
因为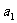 也满足上式,所以数列
也满足上式,所以数列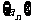 的通项公式为
的通项公式为 (
(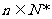 ). ……(4分)
). ……(4分)
(2)由已知 ,
……(5分)
,
……(5分)
因为 是等差数列,可设
是等差数列,可设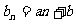 (
(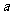 、
、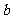 为常数),
…(6分)
为常数),
…(6分)
所以 ,于是
,于是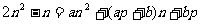 ,
,
所以 , 因为
, 因为 ,所以
,所以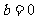 ,
, .
………(8分)
.
………(8分)
(注:用 为定值也可解,可按学生解答步骤适当给分)
为定值也可解,可按学生解答步骤适当给分)
(3) ,
……(10分)
,
……(10分)
所以
……(11分)
由 ,得
,得 ,因为
,因为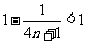 ,所以
,所以 .
.
所以,所求的最小正整数 的值为
的值为 .
……(13分)
.
……(13分)
20(本小题满分13分)
工厂生产某种产品,次品率p与日产量x(万件)间的关系为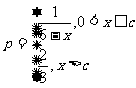 ,
,
 .已知每生产1件合格产品盈利3元,每出现1件次品亏损1.5元.
.已知每生产1件合格产品盈利3元,每出现1件次品亏损1.5元.
(1)将日盈利额y(万元)表示为日产量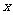 (万件)的函数;
(万件)的函数;
(2)为使日盈利额最大,日产量应为多少万件?(注:次品率= ×100%)
×100%)
(1)当 时,
时,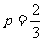 ,
,
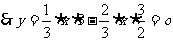 ……1分
……1分
当 ,
,
 ……3分
……3分
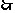 日盈利额y(万元)与日产量x(万件)的函数关系为
日盈利额y(万元)与日产量x(万件)的函数关系为
 …… 6分
…… 6分
(2)由(Ⅰ)知,当 时,日盈利额为0.
时,日盈利额为0.
当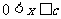 时,
时,
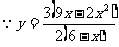 ,
,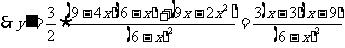 ,
,
令 得
得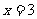 或
或 (舍去)
…… 8分
(舍去)
…… 8分
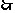 ①当
①当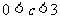 时,
时,
 ,
, 在区间
在区间 上单调递增,
上单调递增,
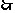
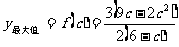 ,此时
,此时 ;
……10分
;
……10分
②当 时,在(0,3)上,
时,在(0,3)上, ,在(3,6)上
,在(3,6)上 ,
,
 ,
,
综上,若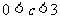 ,则当日产量为c万件时,日盈利额最大;
,则当日产量为c万件时,日盈利额最大;
若 ,则当日产量为3万件时,日盈利额最大
…… 13分
,则当日产量为3万件时,日盈利额最大
…… 13分
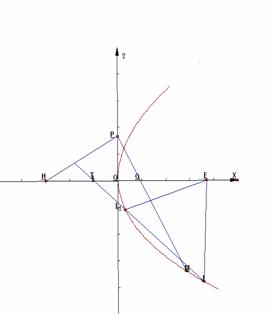
21(本小题满分13分)
如图:已知点 ,点P在y轴上,点Q在x轴的正半轴上,
,点P在y轴上,点Q在x轴的正半轴上,
点M在直线PQ上,且满足 ,
, ,
,
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点 作直线m与轨迹C交于A、B两点,
作直线m与轨迹C交于A、B两点,
若在x轴上存在一点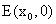 ,使得
,使得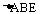 为等边三角形,求
为等边三角形,求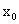 的值.
的值.

 解析(1)设
解析(1)设 ,由
,由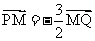 得:
得: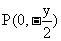 ,
, ,
,
由 得:
得: ,即
,即 ,
,
由点Q在x轴的正半轴上,故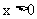 ,
,
即动点M的轨迹C是以 为顶点,以
为顶点,以 为焦点的抛物线,除去原点;……(5分)
为焦点的抛物线,除去原点;……(5分)
(2)设 ,代入
,代入 得:
得:
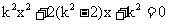 …………①
…………①
设 ,
,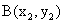 ,则
,则 是方程①的两个实根,
是方程①的两个实根,
则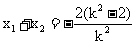 ,
,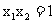 ,所以线段AB的中点为
,所以线段AB的中点为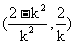 ,……(8分)
,……(8分)
线段AB的垂直平分线方程为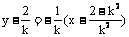 ,
,
令 ,
,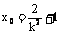 ,得
,得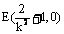 ,
……(10分)
,
……(10分)
因为 为正三角形,则点E到直线AB的距离等于
为正三角形,则点E到直线AB的距离等于 ,
,
又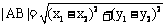 =
=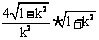 ,
,
所以,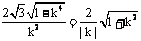 ,解得:
,解得: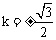 ,
, . ……(13分)
. ……(13分)
18.(本小题满分12分)
在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,
四边形BCC1B1是矩形,且C1B1⊥AB.
(Ⅰ)求证:平面CA1B⊥平面A1AB B1;
(Ⅱ)若C1B1=3,AB=4,∠ABB1=60O,求直线AC1与平面BCC1B1所成角的正弦值.

18(Ⅰ)证明 在三棱柱ABC-A1B1C1中,C1B1//CB,
∵C1B1⊥AB,∴CB⊥AB.
又四边形BCC1B1是矩形,CB⊥B1B,∴CB⊥平面A1AB B1.
而CB 平面CA1B ,故平面CA1B⊥平面A1A
B B1.
平面CA1B ,故平面CA1B⊥平面A1A
B B1.
(Ⅱ)解 过A作AH⊥BB1于H,连C1H.
∵CB⊥平A1AB
B1,CB 平面BC C1B1,
平面BC C1B1,
∴平面BCC1B1⊥平面A1AB B1.
∴AH⊥平面BCC1B1.
∴∠AC1H为AC1与平面BCC1B1所成的角.
连结A1B交于A1B于O,由四边形A1ABB1是菱形, ABB1=60O,
ABB1=60O,
可知△ABB1为等边三角形, AB1=AB =4,而H为BB中点,于是AH=2
在Rt△C1B1A中,
AC1=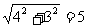 ,
,
在Rt△AH C1中,
故直线AC1与平面BCC1B1所成的角的正弦值为

17.解:

16.解:(1) ………………………3分
………………………3分
由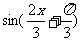 =0即
=0即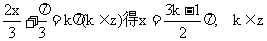
即对称中心的横坐标为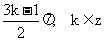 ………………………………………… 6分
………………………………………… 6分
(2)由已知b2=ac知
 ……………………………9分
……………………………9分

 即
即 的值域为
的值域为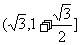 ,
,
综上所述,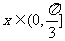 ,
,  的值域为
的值域为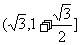 ………………………………12分.
………………………………12分.
17(本小题满分12分)
田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A、B、C,田忌的三匹马分别为a、b、c;三匹马各比赛一次,胜两场者为获胜.若这六匹马比赛优、劣程度可以用以下不等式表示:A>a>B>b>C>c.
(1)如果双方均不知道对方马的出场顺序,求田忌获胜的概率;
(2)为了得到更大的获胜概率,田忌预先派出探子到齐王处打探实情,得知齐王第一场必出上等马.那么,田忌应怎样安排出马的顺序,才能使自己获胜的概率最大?
16.(本小题满分12分)
已知函数 .
.
(1)将f(x)写成 (
(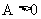 )的形式,并求其图像对称中心的横坐标;
)的形式,并求其图像对称中心的横坐标;
(2)如果△ABC的三边a、b、c满足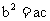 ,且边b所对的角为x,试求x的取值范围及
,且边b所对的角为x,试求x的取值范围及
此时函数f(x)的值域.
15.设函数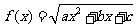
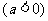 的定义域为
的定义域为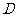 ,值域为
,值域为 .
.
(1)若 则D=
, A= .
则D=
, A= .
(2)若所有点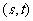
 构成一个正方形区域,则
构成一个正方形区域,则
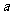 的值为
.
的值为
.
(1)D=[-1,3], A=[0,2].
(2)
14. 右图所给出的是用来求解:
 的程序框图.则在框图
的程序框图.则在框图
的空格(1)处应填入的语句为 ;空格(2)处应填入
的语句为 .
(1) (2)
(2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com