3．“方程ax²+by²＝c表示双曲线”是“ab＜0”的(　)

　 A．充分非必要条件　 　　　　　　　　　　　　 B．必要非充分条件

　 C．充要条件　 　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

　 答案：A

2．已知点F₁(－，0)、F₂(，0)，动点P满足|PF₂|－|PF₁|＝2，当点P的纵坐标是时，点P到坐标原点的距离是(　)

　 A.　 　　　　　　　　　　　 B.　 　　　　　　　　　　 C.　 　　　　　　　　　 D．2

　 解析：由已知条件知P点轨迹是以F₁(－，0)，F₂(，0)为焦点实轴长为2的双曲线的左支，方程为x²－y²＝1(x≤－1)，令y＝可求得x＝－，因此|PO|＝＝.

　 答案：A

1．如果双曲线－＝1上一点P到右焦点的距离等于，那么点P到右准线的距离是(　)

　 A.　 　　　　　　　　 B．13 　　　　　　　　　 C．5　 　　　　　　　　　 D.

　 解析：由－＝1得a＝，b＝2，c＝5，e＝.

　 设P到右准线的距离为d，根据双曲线的定义＝e，即d＝＝.

　 答案：A

5．　 如图，已知点P是以F₁、F₂为焦点的椭圆+＝1(a>b>0)上一点，若PF₁⊥PF₂，

　　 tan∠PF₁F₂＝，则此椭圆的离心率是________．

解析：本题考查椭圆离心率的求法．由题得△PF₁F₂为直角三角形，设|PF₁|＝m，

则tan∠PF₁F₂＝，∴|PF₂|＝，|F₁F₂|＝m，∴e＝＝＝.

4．椭圆+＝1的右焦点为F，设A(－，)，P为椭圆上的动点，则|AP|+ |PF|

　 取得最小值时P点的坐标是(　)

　 A．(，)　 　　　　　　　 B．(5,0)　 　　　　 C．(0,2)　 　 D．(0，－2)或(0,2)

　 答案：A

3．已知如图，椭圆+＝1(a>b>0)上一点P，F₁、F₂为椭圆的焦点，若∠F₁PF₂＝θ，

　 则△PF₁F₂的面积等于(　)

　 A．a²tan　 　　　　　　　　　　　　　　　　　　　　　　　　 B．a²cot

　 C．b²tan 　　　　　　　　　　　　　　　　　　　　　　　　 D．b²cot

　 解析：在△PF₁F₂中，由余弦定理得：2|PF₁|·|PF₂|·cos θ＝|PF₁|²+|PF₂|²－|F₁F₂|²＝

　 (|PF₁|+|PF₂|)²－2|PF₁|·|PF₂|－|F₁F₂|²＝(2a)²－2|PF₁|·|PF₂|－(2c)²(其中c²＝a²－b²)．

　 ∴|PF₁|·|PF₂|·(1+cos θ)＝2b²，∴S△F₁PF₂＝|PF₁|·|PF₂|·sin θ＝··

　 sin θ＝b²tan.

　 答案：C

2．椭圆+＝1的离心率为，则k的值为(　)

　 A．－21　 　　　　　 B．21 　　　　　　 C．－或21　 　　　 D.或21

　 解析：若a²＝9，b²＝4+k，则c＝，由＝即＝得k＝－；

　 若a²＝4+k，b²＝9，则c＝，由＝，即＝，解得k＝21.

　 答案：C

1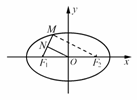．椭圆+＝1上一点M到焦点F₁的距离为2，N是MF₁的中点，则|ON|　　　 　 等于(　)

　 A．2　 　　　　　　　 B．4 　　　　　　　 C．8　 　　　　　　　　　 D.

　 解析：连接MF₂，已知|MF₁|＝2，又|MF₁|+|MF₂|＝10，

　 |MF₂|＝10－|MF₁|＝8，如图，|ON|＝|MF₂|＝4.

　 答案：B

2．已知直线l₁：mx－y＝0，l₂：x+my－m－2＝0.

　 (1)求证：对m的任意实数值，l₁和l₂的交点P在一定圆上；

　 (2)若l₁与定圆另一交点P₁，l₂与定圆另一交点为P₂，求当m在实数范围内取值时，△PP₁P₂的面积的最大值，并求此时l₁的方程．

　 解答：(1)证明：由mx－y＝0，得m＝代入x+my－m－2＝0中得x+y－－2＝0，即x²+y²－y－2x＝0，亦即(x－1)²+(y－)²＝，所以，l₁和l₂的交点在定圆上．

　 (2)由消去y，得(1+m²)x²－(m+2)x＝0，

　 ∴P₁(0,0)，P(，)．∴|P₁P|＝ ＝.

　 由

　 得P₂(2,1)，∵|P₂P|＝ ＝，

　 又∵l₁⊥l₂，∴△PP₁P₂为直角三角形．

　 ∴S△PP₁P₂＝|P₁P|·|P₂P|＝·＝·.

　 令y＝，则(y－2)m²－3m+y+2＝0.①

　 当y≠2时，应有Δ＝(－3)²－4(y－2)(y+2)≥0.得－≤y≤，

　 ∴||的最大值为，∴△PP₁P₂的最大面积为，

　 此时y＝±代入①式中求得m＝3或－.

　 ∴此时l₁的方程为y＝3x或y＝－x.

1．一直线经过点P(－3，－)被圆x²+y²＝25截得的弦长为8，求此弦所在直线方程．

　 解答： (1)当斜率k不存在时，过点P的直线方程为x＝－3，代入x²+y²＝25，得y₁＝4，y₂＝－4.

　 ∴弦长为|y₁－y₂|＝8，符合题意．

　 (2)当斜率k存在时，设所求直线方程为y+＝k(x+3)，即kx－y+3k－＝0.

　 由已知，弦心距|OM|＝ ＝3，∴＝3，解得k＝－.

　 所以此直线方程为y+＝－(x+3)，即3x+4y+15＝0.

　 所以所求直线方程为x+3＝0或3x+4y+15＝0.