
6.(2009·江苏卷)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
|
学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
|
甲班 |
6 |
7 |
7 |
8 |
7 |
|
乙班 |
6 |
7 |
6 |
7 |
9 |
则以上两组数据的方差中较小的一个为s2=________.
解析:x甲=7,s=(12+02+02+12+02)=,x乙=7,s=(12+02+12+02+22)=,
∴s<s,∴方差中较小的一个为s,即s2=.
5.(2009·浙江卷)某个容量为100的样本的频率分布直方图如下,则在区间[4,5)上的数据的频数为________.
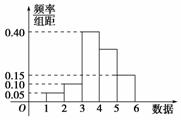
解析:对于在区间[4,5)的的数值为1-(0.4+0.15+0.1+0.05)=0.3,而样本容量为100,因此频数为30.
答案:30
4. (2010·安徽名校联考)关于统计数据的分析,有以下几个结论:
(2010·安徽名校联考)关于统计数据的分析,有以下几个结论:
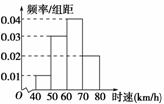
①一组数不可能有两个众数;②将一组数据中的每个数据都减去同一个数后,方差没有变化;③调查剧院中观众观看感受时,从50排(每排人数相同)中任意抽取一排的人进行调查,属于分层抽样;④一组数据的方差一定是正数;⑤如右图是随机抽取的200辆汽车通过某一段公路时的时速分布直方图,根据这个直方图,可以得到时速在[50,60)的汽车大约是60辆.
则这5种说法中错误的个数是( )
A.2 B.3 C.4 D.5
解析:一组数中可以有两个众数,故①错;根据方差的计算法可知②正确;③属于简单随机抽样,故③错误;④错误,因为方差可以是零;⑤正确.故错误的说法有3个.
答案:B
3.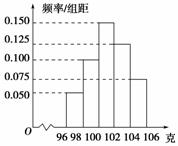 (2009·山东卷)某工厂对一批产品进行了抽样检测,如右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
(2009·山东卷)某工厂对一批产品进行了抽样检测,如右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
A.90 B.75
C.60 D.45
解析:净重小于100克的频率是(0.050+0.100)×2=0.30,故这批产品的个数x满足=0.30,即x=120,净重大于或等于98克且小于104克的频率是(0.100+0.150+0.125)×2=0.75,故所求产品的个数是120×0.75=90.
答案:A
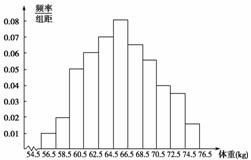
2.为了了解某学校学生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图(如图),根据此图,估计该校2 000名高中男生中体重大于70.5公斤的人数为( )
A.300 B.360 C.420 D.450
解析:图中70.5公斤以上的人数的频率为(0.04+0.035+0.015)×2=0.18,则该校男生体重在70.5公斤以上的人数为2 000×0.18=360.
答案:B
1. (2009·济南二调)如右图是某电视台综艺节目举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
(2009·济南二调)如右图是某电视台综艺节目举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
A.84,4.84 B.84,1.6 C.85,4 D.85,1.6
解析:由茎叶图可知评委打出的最低分为79,最高分为93,其余得分为84,84,86,84,87,故平均分为=85,方差为[3×(84-85)2+(86-85)2+(87-85)2]=1.6.
答案:D
2.一个总体中有100个个体,随机编号0,1,2,…,99,依从小到大的编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=8,则在第8组中抽取的号码是________.
解析:由题意知:m=8,k=8,则m+k=16,也就是第8组的个位数字为6,十位数字为8-1=7,故抽取的号码为76.
答案:76
1.(2010·创新题)某企业三月中旬生产A、B、C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的统计表:
|
产品类别 |
A |
B |
C |
|
产品数量(件) |
|
1
300 |
|
|
样本容量 |
|
130 |
|
由于不小心,表格中A、C产品的有关数据已被污染看不清楚了,统计员只记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C产品的数量是________件.
解析:设样本的总容量为x,则×1 300=130,∴x=300.
∴A产品和C产品在样本中共有300-130=170(件).
设C产品的样本容量为y,则y+y+10=170,∴y=80.∴C产品的数量为×80=800.
答案:800
10.某单位有工程师6人,技术员12人,技工18人,要从这些人中抽取一个容量为n的样本.如果采用系统抽样法和分层抽样法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要在总体中先剔除1个个体,求样本容量n.
解答:总体容量为6+12+18=36.当样本容量是n时,由题意知,系统抽样的间隔为,分层抽样的比例是,抽取工程师×6=(人),抽取技术人员×12=(人),抽取技工×18=(人).所以n应是6的倍数,36的约数即n=6,12,18,36.
当样本容量为(n+1)时,在总体中剔除1人后还剩35人,系统抽样的间隔为,因为必须是整数,所以n只能取6,即样本容量为6.

9.某煤矿有采煤工人400人,运输工人302人,管理和服务人员250人.要从中抽取190人组成职工代表参加讨论奖金分配方案,试确定用何种方法抽取,三种类型的职工各抽多少?
解答:由于奖金分配涉及到各种人的利益不同,所以应采用分层抽样方法.
因为总体人数400+302+250=952(人),=5余2,应剔除2人,而=80(人),=60(人),=50(人),所以采煤工、运输工、管理和服务人员分别抽取80人、60人、50人.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com