
1.(2008年全国Ⅱ理11)等腰三角形两腰所在直线的方程分别为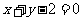 与x-7y-4=0,
与x-7y-4=0,
原点在等腰三角形的底边上,则底边所在直线的斜率为 ( ).
A.3
B.2 C.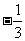 D.
D.
答案 A
解析 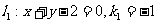 ,
,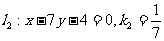 ,设底边为
,设底边为
由题意,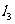 到
到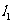 所成的角等于
所成的角等于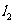 到
到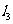 所成的角于是有
所成的角于是有
再将A、B、C、D代入验证得正确答案 是A。
16.(2009江苏卷18)(本小题满分16分)
 在平面直角坐标系
在平面直角坐标系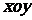 中,已知圆
中,已知圆 和圆
和圆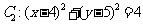 .
.
(1)若直线 过点
过点 ,且被圆
,且被圆 截得的弦长为
截得的弦长为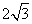 ,求直线
,求直线 的方程;
的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线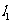 和
和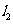 ,它们分别与圆
,它们分别与圆 和圆
和圆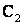 相交,且直线
相交,且直线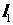 被圆
被圆 截得的弦长与直线
截得的弦长与直线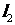 被圆
被圆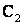 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
解 (1)设直线 的方程为:
的方程为: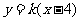 ,即
,即
由垂径定理,得:圆心 到直线
到直线 的距离
的距离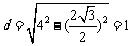 ,
,
结合点到直线距离公式,得:
化简得: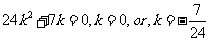
求直线 的方程为:
的方程为: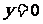 或
或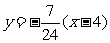 ,即
,即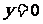 或
或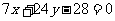
(2) 设点P坐标为 ,直线
,直线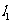 、
、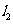 的方程分别为:
的方程分别为:
 ,即:
,即:
因为直线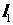 被圆
被圆 截得的弦长与直线
截得的弦长与直线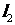 被圆
被圆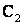 截得的弦长相等,两圆半径相等。
截得的弦长相等,两圆半径相等。
由垂径定理,得::圆心 到直线
到直线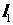 与
与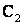 直线
直线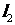 的距离相等。
的距离相等。
故有: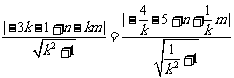 ,
,
化简得:
关于 的方程有无穷多解,有:
的方程有无穷多解,有: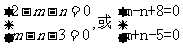
解之得:点P坐标为 或
或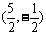 。
。
2005-2008年高考题
15.(江西理16).设直线系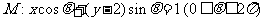 ,对于下列四个命题:
,对于下列四个命题:
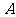 .
.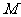 中所有直线均经过一个定点
中所有直线均经过一个定点
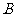 .存在定点
.存在定点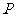 不在
不在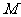 中的任一条直线上
中的任一条直线上
 .对于任意整数
.对于任意整数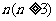 ,存在正
,存在正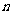 边形,其所有边均在
边形,其所有边均在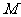 中的直线上
中的直线上
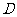 .
.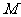 中的直线所能围成的正三角形面积都相等
中的直线所能围成的正三角形面积都相等
其中真命题的代号是 (写出所有真命题的代号).
[解析]因为 所以点
所以点 到
到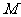 中每条直线的距离
中每条直线的距离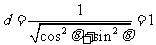
即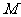 为圆
为圆 :
: 的全体切线组成的集合,从而
的全体切线组成的集合,从而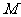 中存在两条平行直线,
中存在两条平行直线,
所以A错误;
又因为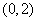 点不存在任何直线上,所以B正确;
点不存在任何直线上,所以B正确;
对任意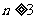 ,存在正
,存在正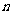 边形使其内切圆为圆
边形使其内切圆为圆 ,故
,故 正确;
正确;
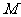 中边能组成两个大小不同的正三角形
中边能组成两个大小不同的正三角形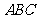 和
和 ,故D错误,
,故D错误,
故命题中正确的序号是 B,C.
[答案]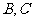
14.(湖北文14)过原点O作圆x2+y2‑-6x-8y+20=0的两条切线,设切点分别为P、Q,
则线段PQ的长为 。
[解析]可得圆方程是 又由圆的切线性质及在三角形中运用正弦定理得
又由圆的切线性质及在三角形中运用正弦定理得 .
.
[答案]4
13.(全国Ⅱ文15)已知圆O: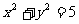 和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于
和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于
[解析]由题意可直接求出切线方程为y-2= (x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和
(x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和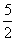 ,所以所求面积为
,所以所求面积为 。
。
[答案]

12.(全国Ⅱ理16)已知 为圆
为圆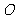 :
: 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为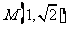 ,则四边形
,则四边形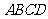 的面积的最大值为
。
的面积的最大值为
。
[解析]设圆心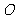 到
到 的距离分别为
的距离分别为 ,则
,则 .
.
四边形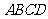 的面积
的面积
[答案]5
11.(全国Ⅰ文16)若直线 被两平行线
被两平行线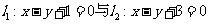 所截得的线段的长为
所截得的线段的长为 ,则
,则 的倾斜角可以是
的倾斜角可以是
①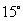 ②
②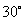 ③
③ ④
④ ⑤
⑤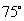
其中正确答案的序号是 .(写出所有正确答案的序号)
[解析]解:两平行线间的距离为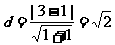 ,由图知直线
,由图知直线 与
与 的夹角为
的夹角为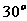 ,
, 的倾斜角为
的倾斜角为 ,所以直线
,所以直线 的倾斜角等于
的倾斜角等于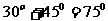 或
或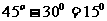 。
。
[答案]①⑤
10. (天津文,14)若圆 与圆
与圆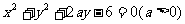 的公共弦长为
的公共弦长为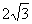 ,则a=________.
,则a=________.
[解析]由已知,两个圆的方程作差可以得到相交弦的直线方程为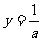 ,
,
利用圆心(0,0)到直线的距离d 为
为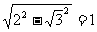 ,解得a=1.
,解得a=1.
[答案]1
9.(天津理,13)设直线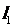 的参数方程为
的参数方程为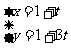 (t为参数),直线
(t为参数),直线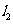 的方程为y=3x+4则
的方程为y=3x+4则 与
与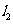 的距离为_______
的距离为_______
[解析]由题直线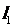 的普通方程为
的普通方程为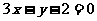 ,故它与与
,故它与与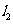 的距离为
的距离为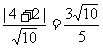 。
。
[答案]
8. (广东文,13)以点(2,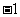 )为圆心且与直线
)为圆心且与直线 相切的圆的方程是
.
相切的圆的方程是
.
[解析]将直线 化为
化为 ,圆的半径
,圆的半径 ,
,
所以圆的方程为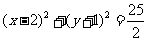
[答案]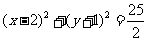
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com