
4.常用词语的否定
|
正面词 |
都是 |
任意的 |
至多有一个 |
至少有一个 |
|
反面词 |
不都是 |
某个 |
至少有两个 |
一个也没有 |
3. 反证法:否定结论,再找矛盾。
2.四种命题,充要条件及判定;
1.要正确理解和运用逻辑联结词“或”、“且”、“非”;
[例1]写出下列命题的逆命题、否命题、逆否命题,并判断真假.
(1)“当abc=0时,a=0或b=0或c=0”
(2) 若
解:(1)原命题即:若abc=0,则a=0或b=0或c=0,是真命题.
逆命题:若a=0或b=0或c=0,则abc=0,是真命题.
否命题:若abc≠0,则a≠0且b≠0且c≠0,是真命题.
逆否命题:若a≠0且b≠0且c≠0,则abc≠0,是真命题.
(2)逆命题:
否命题: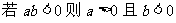
逆否命题: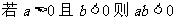
易判定否命题假,逆否命题真,从而,逆命题假,原命题真。
温馨提示:判断命题真假时注意利用等价关系,原命题不易判定时,可判断与之等价的逆否命题真假,如(2)小题。
[例2] 已知抛物线C:y=-x2+mx-1,点M(0,3),
N(3,0),求抛物线C与线段MN有两个不同交点的
(充要)条件。
解:∵线段MN: y= -x+3 (0≤x≤3)
∴有两个不同交点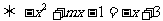
即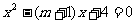 在[0,3]上有两个不等实根
在[0,3]上有两个不等实根


特别提醒:求充要条件本题是进行等价转化,也可先推出必要条件,再验证充分性。
[例3](2003全国)已知 ,设
,设
命题 P:函数 在R上单调递减;
在R上单调递减;
命题Q:不等式 的解集为R。
的解集为R。
如果P和Q有且仅有一个正确,求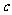 的取值范围
的取值范围
解法1: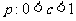 ;
;
又 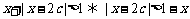
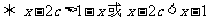

要使解集是R只有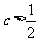 ,即
,即

解法2:函数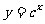 在R上单调递减
在R上单调递减
不等式 的解集为R<=>函数
的解集为R<=>函数
 在R上恒大于1。
在R上恒大于1。


……下同解法1
[研讨.欣赏]用反证法证明:若整数系数一元二次方程:ax2+bx+c=0(a≠0)有有理根,那么a,b,c中至少有一个是偶数。
思路点拨:有有理根则 中的Δ必是完全平方数;研究的是奇偶数问题,就从奇偶上找矛盾。
中的Δ必是完全平方数;研究的是奇偶数问题,就从奇偶上找矛盾。
证明:假设a、b、c都是奇数,则 是完全平方数,且是奇数。
是完全平方数,且是奇数。
设b=2t+1,m=2s+1, 由  得 (b+m)(b-m)=4ac
得 (b+m)(b-m)=4ac
即 (t+s+1)(t-s)=ac,事实上,不论t、s是奇数还是偶数,(t+s+1),(t-s)总有一个是偶数,而ac却是奇数,矛盾,假设不成立。
所以,a、b、c中至少有一个是偶数。
6.可借助文氏图分析。
4. 若苹果在A盒内,则A、B盒上纸条写的为真,不合题意.
若苹果在B盒内,则A、B、D盒上纸条写的为假,C盒上纸条写的为真,符合题意。
2.设p: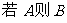 ; 则
; 则 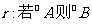 ,
,  …
…
5. (2005湖北卷)对任意实数a,b,c,给出下列命题:
①“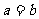 ”是“
”是“ ”充要条件;
”充要条件;
②“ 是无理数”是“a是无理数”的充要条件
是无理数”是“a是无理数”的充要条件
③“a>b”是“a2>b2”的充分条件;
④“a<5”是“a<3”的必要条件.
其中真命题的序号是
6已知 ,命题
,命题 ,则下列
,则下列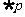 的表述正确的序号是
的表述正确的序号是
①、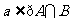 ;
②、
;
②、 ;
;
③、 ; ④、
; ④、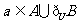 。
。
答案.提示:1-4、BCDB;5、②④; 6、①④
4.有A、B、C、D四个盒子,其中只有一个盒内放有一个苹果,在四个盒子上各有一张纸条.
A盒上纸条写“苹果在此盒内”,
B盒上纸条写“苹果不在此盒内”,
C盒上纸条写“苹果不在A盒内”
D盒上纸条写“苹果在C盒内”。
如果四张纸条中只有一张写的是真的,则苹果必在哪个盒内( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com