
3、下列解说,符合原文意思的一项是( )
A、 抗癌疫苗是一种人的基本遗传物质DNA制成的疫苗。
B、 免疫系统通常情况下不会把癌细胞当作敌人加以攻击。
C、 分裂后失去控制的人体细胞DNA具有基本遗传物质,至少可以阻止癌细胞的繁殖。
D、利用癌症病人的DNA制成的抗癌疫苗,实现了医学家们急于实现的目标。
2、根据文意,对“利用一种新的方法来治疗淋巴细胞 对于治疗所有癌症具有重要的意义”一句,理解正确的一项是( )
A、 淋巴癌包含各类癌症特点,能治疗淋巴癌,也能治疗所有癌症。
B、 各类癌症都产生于人体细胞的分裂,因此治疗淋巴癌的方法也适用于治疗各类癌症。
C、 肿瘤的产生和扩散是由于免疫系统功能受阻,用这种新方法诱导系统,可以治疗各类肿瘤。
D、治疗淋巴癌的新方法如获成功,意味着利用不同的癌症病人的DNA制备的疫苗,可以治疗不同的癌症。
1、根据文意,这种疫苗称为“具有人格化的疫苗”的原因是( )
A、 这种疫苗利用癌症病人的DNA制成。
B、 这种疫苗能刺激人体的免疫系统。
C、 这种疫苗能区分癌细胞和健康细胞。
D、这种疫苗对癌症病人没有副作用。
9.已知函数f(x)在R上为增函数,a,b∈R,对命题“若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”,写出逆命题、逆否命题,判断其真假,并证明你的结论。
解:(1)逆命题是:若f(a)+f(b)≥f(-a)+f(-b),则a+b≥0, 真命题。
用反证法证明:假设a+b<0, 则a<-b, b<-a, ∵f(x)在R上为增函数,则f(a)<f(-b),f(b)<f(-a),
∴f(a)+f(b)<f(-a)+f(-b)这与题设相矛盾,所以逆命题为真。
(2)逆否命题:若f(a)+f(b)<f(-a)+f(-b)则a+b<0,为真命题,因为一个命题等价于它的逆否命题,所以可证明原命题为真命题。
∵a+b≥0, ∴a≥-b, b≥-a,又∵ f(x)在R上是增函数,∴f(a)≥f(-b),f(b)≥f(-a),
∴f(a)+f(b)≥f(-a)+f(-b),原命题成立,所以逆否命题为真。
10. 反证法证明:若a、b、c是正实数,则关于x的方程: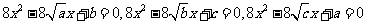 至少有一个方程有两个不相等的实数根。
至少有一个方程有两个不相等的实数根。
证明:假设都没有两个不等实根,则
 ,三式相加得:
,三式相加得: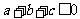 与已知矛盾。
与已知矛盾。
∴至少有一个方程有两个不相等的实数根。
[探索题]在Δ中,∠A、∠B、∠C的对边分别为a、b、c,若 ,求证:∠B必为锐角。
,求证:∠B必为锐角。
证明:假设∠B为直角或钝角,则∠A、∠C必都是锐角,那么
 ,与已知矛盾,故∠B为锐角。
,与已知矛盾,故∠B为锐角。
7.分别写出下列命题的逆命题,否命题,逆否命题,并判断其真假。
(1)若q<1,则方程x2+2x+q=0有实根。
(2)若ab=0,则a=0或b=0。
(3)若x2+y2=0,则x,y全为零。
解析:(1)逆命题:若方程x2+2x+q=0有实根,则q<1,为假命题,
否命题:若q≥1,则方程x2+2x+q=0无实根,假命题。
逆否命题:若方程x2+2x+q=0无实根,则q≥1,真命题。
(2)逆命题:若a=0或b=0, 则ab=0, 真命题。
否命题:若ab≠0,则a≠0且b≠0,真命题。
逆否命题:若a≠0且b≠0,则ab≠0,真命题。
(3)逆命题:若x,y全为零,则x2+y2=0,真命题。
否命题:若x2+y2≠0,则x,y不全为零,真命题。
逆否命题:若x,y不全为零,则x2+y2 0,真命题。
8.已知命题
0,真命题。
8.已知命题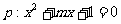 有两个不等的负根;命题
有两个不等的负根;命题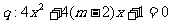 无实根. 若命题p与命题q有且只有一个为真,求实数m的取值范围.
无实根. 若命题p与命题q有且只有一个为真,求实数m的取值范围.
解: 有两个不等的负根,
有两个不等的负根,
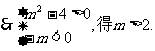
 无实根,
无实根,
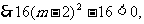 得
得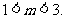
有且只有一个为真,若p真q假,得
若p假q真,得
综合上述得
6.若A是B的必要而不充分条件,C是B的充要条件,D是C的充分而不必要条件,则D是A的 条件。
答案:1-4、BCBB; 5、(1)p且q (2)p或q (3)p且q;6.充分不必要条件(∵D C
C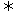 B
B A)
A)
[解答题]
5.分别用“p或q”“p且q”“非p”填空.
(1)命题“15能被3和5整除”是_______________形式;
(2)命题“16的平方根是4或-4”是____________形式;
(3)命题“李强是高一学生,也是共青团员”是_________形式.
3.已知h>0,设命题p为:两个实数a, b满足|a-b|<2h,命题q为:两个实数满足|a-1|<h且|b-1|<h,那么 ( ) A、p是q的充分条件,但不是q的必要条件
B、p是q的必要条件,但不是q的充分条件
C、p是q的充要条件
D、p不是q的充分条件,也不是q的必要条件 4.(2005天津卷)给出下列三个命题
①若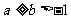 ,则
,则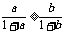
②若正整数m和n满足 ,则
,则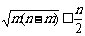
③设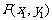 为圆
为圆 上任一点,圆O2以
上任一点,圆O2以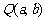 为圆心且半径为1.当
为圆心且半径为1.当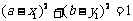 时,圆O1与圆O2相切
时,圆O1与圆O2相切
其中假命题的个数为 ( )
A.0 B.1 C.2 D.3
[填空题]
1.如果命题“p或q”与命题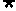 p都是真命题,那么( )。
A、命题p不一定是假命题 B、命题q一定是真命题
C、命题q不一定是真命题 D、命题p与命题q的真假相同
2.下列四个命题中所有真命题是
( )
p都是真命题,那么( )。
A、命题p不一定是假命题 B、命题q一定是真命题
C、命题q不一定是真命题 D、命题p与命题q的真假相同
2.下列四个命题中所有真命题是
( )
①“若xy=1,则x、y互为倒数”的逆命题 ②“面积相等的三角形全等”的否命题 ③“若m≤1,则方程x2-2x+m=0有实根”的逆否命题
④“若A∩B=B,则A B”的逆否命题
B”的逆否命题
A.①② B.②③ C.①②③ D.③④
5.题型.思想.方法:
(1)判断 “ ”真,需要证明或说明;
”真,需要证明或说明;
而判断“

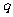 ”假,只要举出一个反例即可。
”假,只要举出一个反例即可。
(2)当判断一个命题的真假有困难时,可转化为其等价命题的真假。
(3)求充要条件可进行等价转化,也可先推出必要条件,再验证充分性。
同步练习 1.2 简易逻辑
[选择题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com