
4.(2004全国Ⅰ)已知a、b为不垂直的异面直线,α是一个平面,则a、b在α上的射影有可能是
①两条平行直线;
②两条互相垂直的直线;
③同一条直线;
④一条直线及其外一点.
在上面结论中,正确结论的编号是__________.(写出所有正确结论的编号)
3.设线段AB、CD是夹在两平行平面a、b之间的异面线段,点A、CÎa,B、DÎb,若M、N分别是AB、CD的中点,则有 ( )
A.MN= (AC+BD B.MN>
(AC+BD B.MN> (AC+BD)
(AC+BD)
C.MN<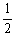 (AC+BD)
(AC+BD)
D.MN与 (AC+BD)大小关系不确定.
(AC+BD)大小关系不确定.
[填空题]
2.(2005年高考·湖北卷·文8)已知a、b、c是直线, 是平面,给出下列命题:
是平面,给出下列命题:
①若 ;
;
②若 ;
;
③若 ;
;
④若a与b异面,且 相交;
相交;
⑤若a与b异面,则至多有一条直线与a,b都垂直.其中真命题的个数是( )
A.1 B.2 C.3 D.4
1.a、b是两个不重合平面,l,m是两条不重合直线,那么a∥b的一个充分条件是( )
A.lÌa,mÌa,l∥b,m∥b
B.lÌa,mÌb,l∥m
C.l⊥a,m⊥b,l∥m
D.l∥a,m∥b,l∥m
3.解题中,要注意灵活地实施下面的转化: 线线ó线面ó面面;立体几何ó平面几何;从而使问题简
同步练习 9.2线面平行、面面平行
2.证明两平面平行的常用方法:
1.直线和平面平行的判定方法:
[例1]:如图,设a,b是异面直线,AB是a,b的公垂线,过AB的中点O作平面α与a,b分别平行,M,N分别是a,b上的任意两点,MN与α交于点P,求证P是MN的中点.
证明:连接AN,交平面α与点Q,连PQ,
∵b∥α,bÌ平面ABN,平面ABN∩α=OQ,
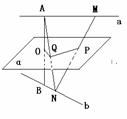
∴b∥OQ,又O为AB的中点,
∴Q为AN的中点.
∵a∥α,aÌ平面AMN且平面AMN∩α=PQ
∴a∥PQ. ∴P为MN的中点.
[例2]如图,四面体A-BCD被一平面所截,截面EFGH是一个矩形.
(1)求证:CD∥平面EFGH.
(2)求异面直线AB、CD所成的角.
(3)若AB=a,CD=b,
求截面EFGH面积的最大值. 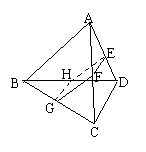
(1)证明:∵截面EFGH是一个矩形,
∴EF∥GH, 又GHÌ平面BCD.
∴EF∥面BCD,而EFÌ面ACD,
面ACD∩面BCD=CD.
∴EF∥CD,∴CD∥平面EFGH.
(2)解:由(1)知CD∥EF,同理AB∥FG,由异面直线所成角的定义知∠EFG即为所求的角.易得∠EFG=90°. (3)答案:ab/4
◆思悟提炼:灵活进行:“线线平行ó线面平行”.
[例3] 已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM∶MA=BN∶ND=5∶8.
(1)求证:直线MN∥平面PBC;
(2)求直线MN与平面ABCD所成的角


证明(1):∵P-ABCD是正四棱锥,
∴ABCD是正方形.连结AN并延长交
BC于点E,连结PE.
∵AD∥BC,∴EN∶AN=BN∶ND.
又∵BN∶ND=PM∶MA,
∴EN∶AN=PM∶MA.
∴MN∥PE.又∵PE在平面PBC内,
∴MN∥平面PBC.
解(2):由(1)知MN∥PE,
∴求MN与平面ABCD所成的角即可.
作PO⊥面ABCD于O,连结OE,则∠PEO为PE与平面ABCD所成的角.
由正棱锥的性质知
PO=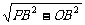 =
= .
.
由(1)知,BE∶AD=BN∶ND=5∶8,
∴BE= .
.
在△PEB中,∠PBE=60°,
PB=13,BE= ,
,
根据余弦定理,得PE=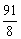 .
.
在Rt△POE中,PO= ,PE=
,PE=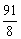 ,
,
∴sin∠PEO=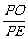 =
= .
.
故MN与平面ABCD所成的角为arcsin .
.
◆思悟提炼:证线面平行,一般是转化为证线线平行.
求直线与平面所成的角一般是作出线与面所成的角-转化为一个平面内的线线角.
[例4]如下图,在正方体ABCD-A1B1C1D1中,AB=a.
(1)求证:平面AD1B1∥平面C1DB;
(2)求证:A1C⊥平面AD1B1;
(3)求平面AB1D1与平面BC1D间的距离.
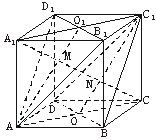
(1)
证明:∵D1B1∥DB,∴D1B1∥平面C1DB.同理,AB1∥平面C1DB.
又D1B1∩AB1=B1,∴平面AD1B1∥平面C1DB.
(2)证明:∵A1C1⊥D1B1,而A1C1为A1C在平面A1B1C1D1上的射影,∴A1C1⊥D1B1. 同理,A1C⊥AB1,D1B1∩AB1=B1.
∴A1C⊥平面AD1B1.
(3)解:设A1C∩平面AB1D1=M,
A1C∩平面BC1D=N,O1、O分别为上底面A1B1C1D1、下底面ABCD的中心. 则M∈AO1,N∈C1O,且AO1∥C1O,MN的长等于平面AD1B1与平面C1DB的距离,即MN=A1M=NC= A1C=
A1C= a.
a.
6. 平面ABC、平面ABD
6.在四面体ABCD中,M、N分别是面△ACD、△BCD的重心,则四面体的四个面中与MN平行的是________.
◆答案提示:1-4.CBCD; 5. 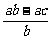 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com