
2.数学思想方法是支撑数学试卷的骨架.
(1)合情推理是培养创新意识的一种途径和手段.
理(10)定义在R上的函数f(x)满足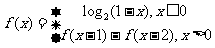 ,则f(2009)的值为
,则f(2009)的值为
(A) -1 (B) 0 (C) 1 (D) 2
解析:本小题主要考查分段函数的概念及归纳(合情)推理的方法.
由已知得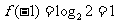 ,
,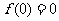 ,
, ,
,
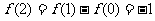 ,
,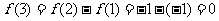 ,
,
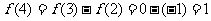 ,
,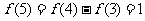 ,
,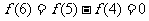 ,
,
文(7)定义在R上的函数f(x)满足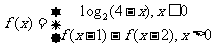 ,则f(3)的值为
,则f(3)的值为
(A) -1 (B) -2 (C) 1 (D) 2
解析:此题是理科(10)的姊妹题.本小题主要考查分段函数的概念及归纳(合情)推理的方法.答案为(B).
文(5)在R上定义运算⊙:a⊙b= a b+2 a+ b,则满足x⊙(x─2)<0的实数x的取值范围为
(A)(0,2) (B) (-2,1) (C)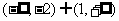 (D) (-1,2)
(D) (-1,2)
解析:本小题主要考查类比(合情)推理与解一元二次不等式.答案为(B).
(2)数形结合是求解数学问题的有效方法和工具.
理(11)在区间[-1,1]上随机取一个数x,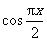 的值介于0到
的值介于0到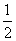 之间的概率是
之间的概率是
(A) 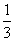 (B)
(B) 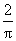 (C)
(C) 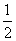 (D)
(D) 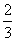
解析:本小题主要考查利用余弦函数值构造几何概型.
在区间[-1,1]上随机取一个数x,即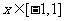 时,
时,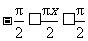 ,
,
因为 当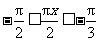 或
或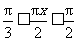 时,
时,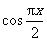 的值介于0到
的值介于0到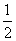 ,
,
所以 根据几何概型的意义,两个区间长度之比为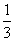 ,故答案为(A).
,故答案为(A).
文(11)在区间[-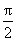 ,
,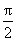 ]上随机取一个数x,
]上随机取一个数x,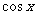 的值介于0到
的值介于0到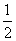 之间的概率是
之间的概率是
(A) 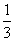 (B)
(B) 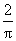 (C)
(C) 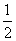 (D)
(D) 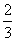
解析:此题是理科(11)的姊妹题.本小题主要考查利用余弦函数值构造几何概型.答案为(A).
 理(12)设x,y满足约束条件
理(12)设x,y满足约束条件 若目标函数
若目标函数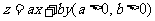 的最大值为12,则
的最大值为12,则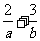 的最小值为
的最小值为
(A) 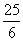 (B)
(B) 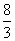 (C)
(C) 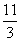 (D) 4
(D) 4
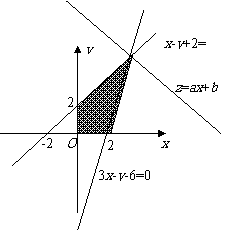
解析:本小题主要考查线性规划与基本(均值)不等式的应用和运算能力,考查数形结合的数学方法.
不等式表示的平面区域如图所示阴影部分,当直线ax+by= z(a>0,b>0)过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,目标函数z=ax+by(a>0,b>0)取得最大值12,即4a+6b=12,即2a+3b=6,
而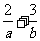 =
=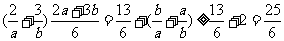 ,故答案为(A).
,故答案为(A).
 理文(14)若函数
理文(14)若函数 且
且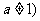 有两个零点,则实数a的取值范围
有两个零点,则实数a的取值范围
是 .
解析:本小题主要考查图像法解函数零点问题.答案为(1, ).
).
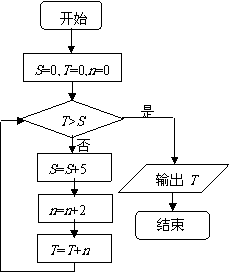
理文(15)执行右边的程序框图,输出的T= .
解析:本小题主要考查循环结构框图应用.答案为30.
理(16)已知定义在R上的奇函数f(x)满足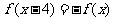 ,且在区间[0,2]上是增函数.若方程
,且在区间[0,2]上是增函数.若方程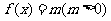 在区间[-8,8]上有四个不同的根
在区间[-8,8]上有四个不同的根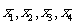 ,则
,则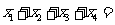 .
.
解析:本小题主要考查抽象函数的周期性(对称性)和单调性,以及数形结合的数学思想方法.
因为 定义在R上的奇函数,满足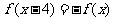 ,所以
,所以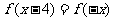 ,
,
所以 函数图象关于直线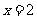 对称且
对称且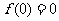 .
.
由 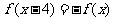 ,知
,知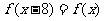 ,所以函数又是以8为周期的周期函数,
,所以函数又是以8为周期的周期函数,
又因为 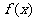 在区间[0,2]上是增函数,所以
在区间[0,2]上是增函数,所以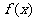 在区间[–2,0]上也是增函数.
在区间[–2,0]上也是增函数.
由对称性知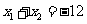
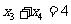 ,所以
,所以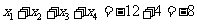 .故答案为 -8.
.故答案为 -8.
文(12)已知定义在R上的奇函数f(x)满足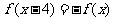 ,且在区间[0,2]上是增函数,则
,且在区间[0,2]上是增函数,则
(A) f(-25)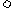 f(11)
f(11)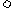 f(80) (B) f(80)
f(80) (B) f(80) 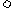 f(11)
f(11)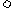 f(-25)
f(-25)
(C) f(11)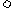 f(80)
f(80)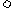 f(-25) (D) f(-25)
f(-25) (D) f(-25)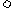 f(80)
f(80)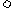 f(11)
f(11)
解析:此题是理科(16)的姊妹题.本小题主要考查抽象函数的周期性(对称性)和单调性.答案为(D).
文(16)某公司租赁甲、乙两种设备生产A、B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元.现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为 元.
解析:本小题主要考查线性规划的应用以及运算能力.答案为2300.
(3)转化与化归是最普遍的数学思想方法.
理(17)设函数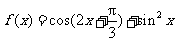 .
.
(Ⅰ)求函数f(x)的最大值和最小正周期;(5分)
(Ⅱ)设A,B,C分别为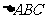 的三个内角,若
的三个内角,若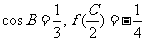 且C为锐角,求
且C为锐角,求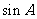 .
.
解析:本小题主要考查两角和的余弦和正弦、二倍角公式及三角函数的最值和周期的概念.
(Ⅰ)法一:f(x)=cos(2x+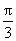 )+sin
)+sin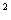 x=
x=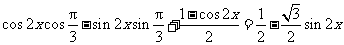 .
.
所以函数f(x)的最大值为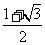 ,最小正周期
,最小正周期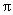 .
.
法二:“导数法”.
(Ⅱ)f(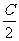 )=
)=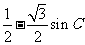 =-
=-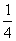 ,所以
,所以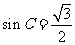 ,又因为C为锐角,所以
,又因为C为锐角,所以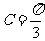 ,
,
 所以sinA =
所以sinA =
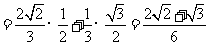 .
.
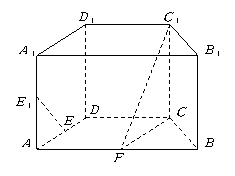
理(18)如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰三角形,AB//CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.
(Ⅰ)证明:直线EE1//平面FCC1;(6分)
(Ⅱ)求二面角B-F C1-C的余弦值.
解析:本小题主要考查底面为等腰梯形的直四棱柱中的线面平行及求二面角问题(传统方法较易).
理(19)在某学校组织的一次篮球定点投篮训练中,规定每人最多投三次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次.某同学在A处的命中率q1为0.25,在B处的命中率为q2.该同学选择先在A处投一球,然后都在B处投,用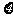 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
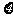 |
0 |
2 |
3 |
4 |
5 |
|
P |
0.03 |
P1 |
P2 |
P3 |
P4 |
(Ⅰ)求q2的值;(3分)
(Ⅱ)求随机变量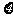 的数学期望E
的数学期望E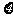 ;(8分)
;(8分)
(Ⅲ)是比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
解析:本小题主要考查随机变量的概率分布与数学期望在定点投篮问题中的应用.
(Ⅰ)设该同学在A处投中为事件A,在B处投中为事件B,则事件A,B相互独立,且P(A)=0.25,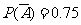 , P(B)= q
, P(B)= q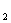 ,
,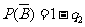 .
.
根据分布列知: 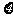 =0时,
=0时,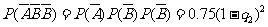 =0.03,
=0.03,
所以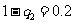 ,q
,q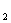 =0.8.
=0.8.
(Ⅱ)当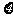 =2时, P1=
=2时, P1=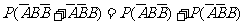
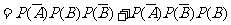 =0.75 q
=0.75 q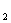 (
(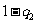 )×2=1.5 q
)×2=1.5 q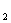 (
(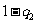 )=0.24,
)=0.24,
当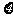 =3时, P2 =
=3时, P2 =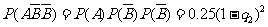 =0.01,
=0.01,
当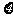 =4时, P3=
=4时, P3=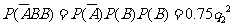 =0.48,
=0.48,
当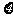 =5时, P4=
=5时, P4=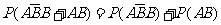
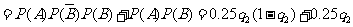 =0.24.
=0.24.
所以随机变量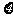 的分布列为
的分布列为 

 |
0
|
2
|
3 |
4 |
5 |
|
P
|
0.03
|
0.24
|
0.01 |
0.48
|
0.24
|
随机变量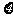 的数学期望
的数学期望 .
.
(Ⅲ)该同学选择都在B处投篮得分超过3分的概率为
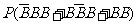
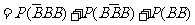
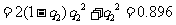 ;
;
该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72.
由此看来该同学选择都在B处投篮得分超过3分的概率大.
理(20)等比数列{an}的前n项和为Sn,已知对于任意的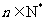 ,点(n, Sn)均在函数
,点(n, Sn)均在函数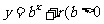 且
且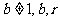 均为常数)的图像上.
均为常数)的图像上.
(Ⅰ)求r的值;(4分)
(Ⅱ)当b=2时,记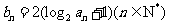 .
.
证明:对于任意的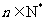 ,不等式
,不等式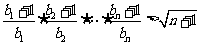 成立.
成立.
解析:本小题主要考查等比数列的概念与不等式证明(数学归纳法或放缩法).
(Ⅰ)因为对任意的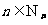 ,点
,点 均在函数
均在函数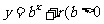 且
且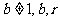 均为常数的图像上.所以得
均为常数的图像上.所以得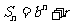 ,
,
当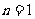 时,
时,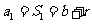 ,
,
当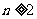 时,
时,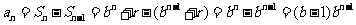 ,
,
又因为{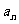 }为等比数列,所以
}为等比数列,所以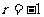 ,公比为
,公比为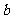 ,
,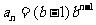 .
.
(Ⅱ)当b=2时,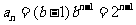 ,
, 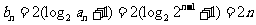 .
.
则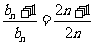 ,所以
,所以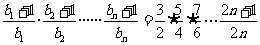 .
.
可以用数学归纳法或放缩法证明不等式:
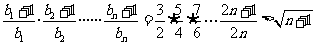 成立. 以下略.
成立. 以下略.
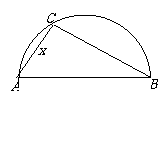
理(21)两县城A和B相距20公里,先计划在两县城外以AB为直径的半圆弧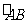 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与对城B的影响度之和.记C点到城A的距离为xkm,建在C处的垃圾处理厂对城A和城B的总影响度为y.统计表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4,对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k.当垃圾处理厂建在弧
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与对城B的影响度之和.记C点到城A的距离为xkm,建在C处的垃圾处理厂对城A和城B的总影响度为y.统计表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4,对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k.当垃圾处理厂建在弧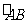 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.
(Ⅰ)将y表示成x的函数;(6分)
(Ⅱ)讨论(Ⅰ)中函数的单调性,并判断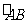 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由.
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由.
解析:本小题主要考查函数应用问题,垃圾处理厂的选点对两城市的影响度、反比概念和导数求极值的方法.
(Ⅰ)如图,由题意知AC⊥BC,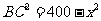 ,
,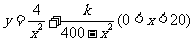 ,
,
 其中当
其中当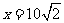 时,y=0.065,所以k=9.
时,y=0.065,所以k=9.
所以y表示成x的函数为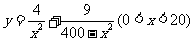 .
.
(Ⅱ)法一:利用导数求函数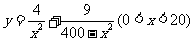 的最小值.
的最小值.
法二:令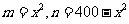 ,则
,则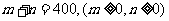 .
.
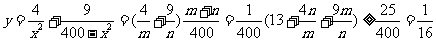 .
.
理(22)设椭圆E: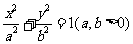 过
过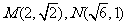 两点,O为坐标原点.
两点,O为坐标原点.
(Ⅰ)求椭圆E的方程;(3分)
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且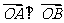 ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求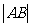 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
解析:本小题主要考查待定系数法求椭圆方程,圆的方程与切线,垂直的概念及方法,弦长的最值问题.
(Ⅰ)因为椭圆E: 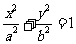 (a,b>0)过M(2,
(a,b>0)过M(2,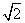 ),N(
),N(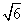 ,1)两点,
,1)两点,
所以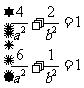 解得
解得 所以
所以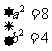
椭圆E的方程为 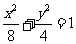 .
.
(Ⅱ)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且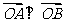 .
.
法一:设该圆的切线方程为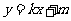 ,
,
解方程组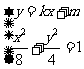 得
得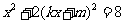 ,即
,即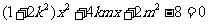 ,
,
则△= , 即
, 即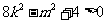 .
.
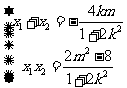 ,
,
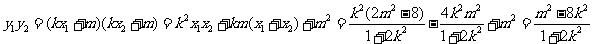 要使
要使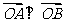 ,需使
,需使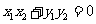 ,即
,即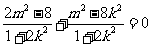 ,
,
所以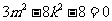 ,所以
,所以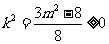 .
.
又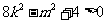 ,所以
,所以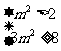 ,所以
,所以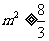 ,即
,即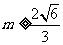 或
或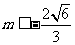 .
.
因为直线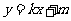 为圆心在原点的圆的一条切线,所以圆的半径为
为圆心在原点的圆的一条切线,所以圆的半径为
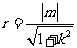 ,
,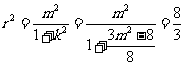 ,
,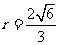 ,
,
所求的圆为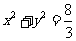 ,此时圆的切线
,此时圆的切线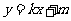 都满足
都满足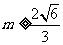 或
或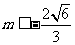 ,
,
而当切线的斜率不存在时切线为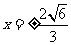 与椭圆
与椭圆 的两个交点为
的两个交点为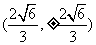 或
或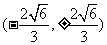 ,满足
,满足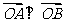 .
.
综上, 存在圆心在原点的圆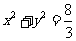 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且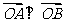 .
.
推广:设椭圆E: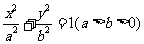 ,O为坐标原点.
,O为坐标原点.
(Ⅰ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且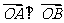 ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求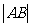 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(Ⅱ)设直线l与圆C: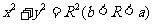 相切于A1,且l与椭圆E只有一个公共点B1.当R为何值时,
相切于A1,且l与椭圆E只有一个公共点B1.当R为何值时,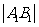 取得最大值?并求最大值.
取得最大值?并求最大值.
文(22)设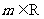 ,在平面直角坐标系中,已知向量a=(mx,y+1),向量b=(x,y-1),a
,在平面直角坐标系中,已知向量a=(mx,y+1),向量b=(x,y-1),a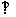 b,动点M(x,y)的轨迹为E.
b,动点M(x,y)的轨迹为E.
(Ⅰ)求轨迹E的方程,并说明该方程所表示曲线的形状;(5分)
(Ⅱ)已知m=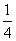 .证明:存在圆心在坐标原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA
.证明:存在圆心在坐标原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且OA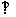 OB(O为坐标原点),并求该圆的方程;(4分)
OB(O为坐标原点),并求该圆的方程;(4分)
(Ⅲ)已知m=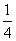 .设直线l与圆C:
.设直线l与圆C: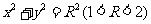 相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,
相切于A1,且l与轨迹E只有一个公共点B1.当R为何值时,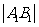 取得最大值?并求最大值.
取得最大值?并求最大值.
解析:本小题主要考查平面向量的数量积运算与含参数的二元二次方程类型的讨论(难于理科同题);圆的方程与切线,垂直的概念及方法;圆与椭圆公切线长的问题.
(Ⅰ)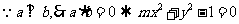 .
.
因此,轨迹E的方程为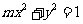 .
.
文(17)已知函数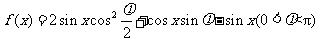 在
在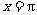 处取最小值.
处取最小值.
(Ⅰ)求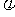 的值;(6分)
的值;(6分)
(Ⅱ)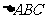 中,a,b,c分别是角A,B,C的对边.已知a=1,b=
中,a,b,c分别是角A,B,C的对边.已知a=1,b=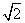 ,
,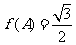 ,求角C.
,求角C.
解析:本小题主要考查两角和的三角函数与倍角公式,弦函数的最值,由三角函数值求角(学生最易出错的问题之一),正弦定理的应用(第(Ⅱ)小题两解,难于理科对应题).
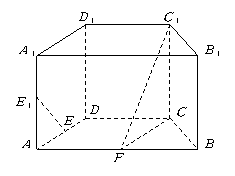 文(18)如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰三角形,AB//CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
文(18)如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰三角形,AB//CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
(Ⅰ)设F是棱AB的中点,证明:直线EE1//平面FCC1;(6分)
(Ⅱ)证明:平面D1AC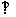 平面BB1C1C.
平面BB1C1C.
解析:理科(18)姊妹题.本小题主要考查空间线面平行与垂直的位置关系和推理论证能力.
文(19)一汽车厂生产A、B、C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
z |
|
标准型 |
300 |
450 |
600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(Ⅰ)求z的值;(3分)
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;(8分)
(Ⅲ)用随机抽样的方法从类舒适型轿车中抽取8辆,经检验它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
解析:本小题主要考查分层抽样的方法与古典概型的应用.
文(20)等比数列{an}的前n项和为Sn,已知对于任意的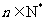 ,点(n, Sn)均在函数
,点(n, Sn)均在函数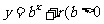 且
且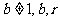 均为常数)的图像上.
均为常数)的图像上.
(Ⅰ)求r的值;(6分)
(Ⅱ)当b=2时,记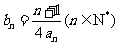 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
解析:理科(20)的姊妹题.本小题主要考查等比数列的概念与数列的错项求和.
文(21)已知函数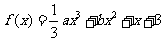 ,其中
,其中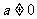 .
.
(Ⅰ)当a,b满足什么条件时,f(x)取得极值?(6分)
(Ⅱ)已知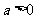 ,且f(x)在区间(0,1]上单调递增,试用a表示出b的取值范围.
,且f(x)在区间(0,1]上单调递增,试用a表示出b的取值范围.
解析:本小题主要考查三次函数的极值存在(导函数的零点)问题,双参数的函数(双曲)最值问题.
(Ⅰ)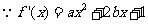 ,
,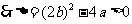 ,即
,即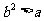 时函数f(x)取得极值.
时函数f(x)取得极值.
不讨论 的情况,不扣分.但是要分
的情况,不扣分.但是要分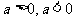 讨论.
讨论.
(Ⅱ)由题意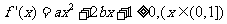 恒成立.
恒成立.
解法一: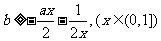 ,令
,令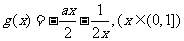 .
.
下面只要求出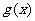 的最大值即可.
的最大值即可.
解法二: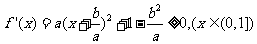 .
.
下面只要求出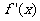 的最小值即可.
的最小值即可.
1.基本数学知识与方法是构成数学试卷的主体.
理文(1) 集合 ,若
,若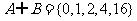 ,则a的值为
,则a的值为
(A)0 (B)1 (C)2 (D)4
解析:本小题主要考查集合的概念与并集运算,实际解答用代入法求解比较快捷.这道题说考知识,不如说考选择题的解法.分别用选择支中的答案去试,很容易排除(A)、(B)、(C),故答案为(D).
理文(2) 复数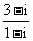 等于
等于
(A) (B)
(B) 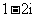 (C)
(C) 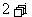 (D)
(D) 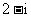
解析:本小题主要考查复数除法运算.答案为(C).
理文(3)将函数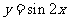 的图像向左平移
的图像向左平移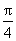 个单位,再向上平移1个单位,所得图像的函数解析式是
个单位,再向上平移1个单位,所得图像的函数解析式是
(A) (B)
(B) 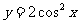
(C) 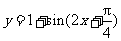 (D)
(D) 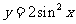
解析:本小题主要考查三角函数图像平移、诱导公式与二倍角公式,考生可能会受选择支(C)的干扰.
将函数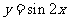 的图像向左平移
的图像向左平移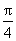 个单位,再向上平移1个单位,所得图像的函数解析式是
个单位,再向上平移1个单位,所得图像的函数解析式是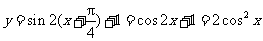 ,答案为(B).
,答案为(B).
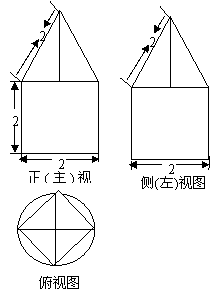
理文(4)一空间几何体的三视图如图所示,则该几何体的体积为
 (A)
(A) (B)
(B) 
(C) 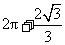 (D)
(D) 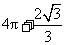
解析:本小题主要考查空间几何体的三视图与体积计算.此几何体是上部为一个底边长为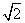 ,高为
,高为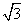 的正四棱锥,下部为一个高为2的等边圆柱.答案为(C).
的正四棱锥,下部为一个高为2的等边圆柱.答案为(C).
理(5)文(9)已知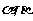 表示两个不同的平面,m为平面
表示两个不同的平面,m为平面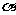 内的一条直线,则“
内的一条直线,则“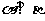 ”是“
”是“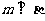 ”的
”的
(A) 充分不必要条件 (B) 必要不充分条件
(C) 充要条件 (D) 既不充分也不必要条件
解析:本小题主要考查空间线面位置关系与充要条件.答案为(B).
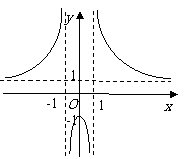
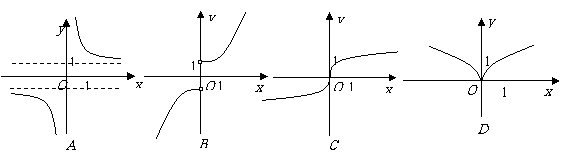 理文(6)函数
理文(6)函数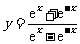 的图像大致为
的图像大致为
解析:本小题主要考查分式复合函数的图像性质.
 因为
因为 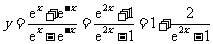 ,
,
显然函数为奇函数,且当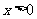 时,函数为减函数.故答案为(A).
时,函数为减函数.故答案为(A).
原型题:(1)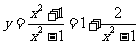 ;
;
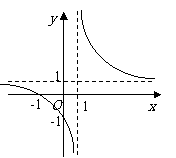 (2)
(2)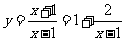 .
.
理(7)文(8)设P是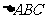 所在平面内的一点,
所在平面内的一点,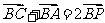 ,则
,则
 (A)
(A) 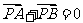 (B)
(B) 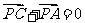
(C) 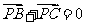 (D)
(D) 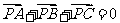
解析:本小题主要考查平面向量的加法运算.由题设P是AC边的中点,故答案为(B).
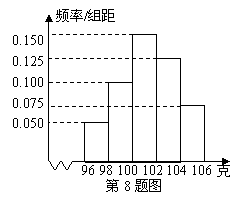
理(8)某工厂对一批产品进行了抽样检测右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98), [98.100),[100.102),[102,104),[104.106].已知样本产品净重小于100克的个数是36,则样本中净重大于或等于98克且小于104克的产品个数是
(A) 90 (B) 75 (C) 60 (D) 45
解析:本小题主要考查频率分布直方图的应用.答案为(A).
理(9)设双曲线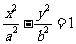 的一条渐近线与抛物线
的一条渐近线与抛物线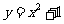 只有一个公共点,则双曲线的离心率为
只有一个公共点,则双曲线的离心率为
(A) 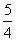 (B) 5 (C)
(B) 5 (C) 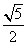 (D)
(D) 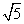
解析:本小题主要考查双曲的渐近线、离心率的概念,直线与抛物线只有一个公共点(相切)的概念及方法.答案为(D).
双曲线 的一条渐近线为
的一条渐近线为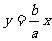 ,
,
由方程组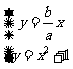 ,消去y,得
,消去y,得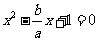 有唯一解,所以△=
有唯一解,所以△=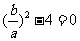 ,
,
所以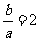 ,
,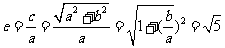 .
.
文(10)设斜率为2的直线l过抛物线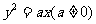 的焦点F,且和y轴交于点A.若
的焦点F,且和y轴交于点A.若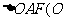 为坐标原点)的面积为4,则抛物线方程为
为坐标原点)的面积为4,则抛物线方程为
(A)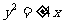 (B)
(B) 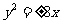 (C)
(C) 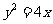 (D)
(D) 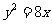
解析:本小题主要考查直线与抛物线方程、直线的斜率和抛物线焦点的概念,三角形面积计算.答案为(B).
文(13)在等差数列{an}中,a3=7,a5= a2+6,则a6= .
解析:本小题主要考查等差数列的概念.答案为13.
理(13)不等式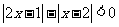 的解集为
.
的解集为
.
解析:本小题主要考查绝对值不等式(选修4-5)的解法.显然移项后,不等式两边平方的解法较简单.答案为(-1,1).
1.试卷的主要参数
表1:知识点分布表
表2:文理科试题比较
表3:卷二成绩分布表
|
|
二 |
17 |
18 |
19 |
20 |
21 |
22 |
合计 |
||
|
文科 |
09 |
均分 |
9.44 |
5.67 |
7.4 |
6.78 |
2.87 |
1.98 |
1.71 |
35.85 |
|
难度 |
0.59 |
0.47 |
0.62 |
0.57 |
0.24 |
0.17 |
0.12 |
0.40 |
||
|
08 |
均分 |
10.2 |
7.01 |
8.23 |
7.28 |
2.61 |
3.97 |
1.33 |
40.66 |
|
|
难度 |
0.64 |
0.58 |
0.69 |
0.61 |
0.22 |
0.33 |
0.10 |
0.45 |
||
|
理科 |
09 |
均分 |
8.65 |
9.31 |
8.19 |
6.20 |
3.17 |
3.79 |
3.51 |
42.82 |
|
难度 |
0.54 |
0.78 |
0.68 |
0.52 |
0.26 |
0.32 |
0.25 |
0.48 |
||
|
08 |
均分 |
11.37 |
7.95 |
8.39 |
4.09 |
5.41 |
2.62 |
2.14 |
41.96 |
|
|
难度 |
0.71 |
0.66 |
0.70 |
0.34 |
0.45 |
0.22 |
0.15 |
0.47 |
5.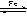 1,2,3,4-四氢化萘的结构简式是
,分子式是C10H12。常温下为无色液体,有刺激性气味,沸点207℃,不溶于水,是一种优良的溶剂,它与液溴发生反应:C10H12+4Br2 C10H8Br4+4HBr。生成的四溴化萘常温下为固态,不溶于水。有人用四氢化萘、液溴、蒸馏水和纯铁粉为原料,制备少量饱和氢溴酸溶液,实验步骤如下:①按一定质量比把四氢化萘和水加入适当的容器中,加入少量纯铁粉。②慢慢滴入液溴,不断搅拌,直到反应完全。③取下反应容器,补充少量四氢化萘,直到溶液颜色消失。过滤,将滤液倒入分液漏斗,静置。④分液,得到的“水层”即氢溴酸溶液。
1,2,3,4-四氢化萘的结构简式是
,分子式是C10H12。常温下为无色液体,有刺激性气味,沸点207℃,不溶于水,是一种优良的溶剂,它与液溴发生反应:C10H12+4Br2 C10H8Br4+4HBr。生成的四溴化萘常温下为固态,不溶于水。有人用四氢化萘、液溴、蒸馏水和纯铁粉为原料,制备少量饱和氢溴酸溶液,实验步骤如下:①按一定质量比把四氢化萘和水加入适当的容器中,加入少量纯铁粉。②慢慢滴入液溴,不断搅拌,直到反应完全。③取下反应容器,补充少量四氢化萘,直到溶液颜色消失。过滤,将滤液倒入分液漏斗,静置。④分液,得到的“水层”即氢溴酸溶液。
回答下面问题:
(1)下面示意图中的装置,适合步骤①和②操作的是 ;
(2)步骤②中如何判断“反应完全” ;
(3)步骤③中补充少量四氢化萘的目的是 ;
(4)步骤③中过滤后得到的固体物质是 ;
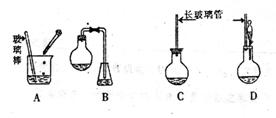
(5)已知在实验条件下,饱各氢溴酸水溶液中氢溴酸的质量分数是66%,如果溴化反应进行完全,则步骤①中四氢化萘和水的质量比约是1: (保留小数点后1位)。
|
Cu2(OH)2CO3·xH2O 2CuO+CO2↑+(x+1)H2O
现取一定量该粉末(未精确测定质量)样品,用下图所列仪器(夹持、加热等仪器均略)先后进行两个实验:
(Ⅰ)测定该粉末组成中结晶水的x值;
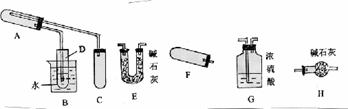 (Ⅱ)用前一个实验结束后的残留固体与乙醇蒸气反应(该残留固体可使乙醇发生去氢氧化),并检验反应产物。(已知乙醇的沸点为78℃)
(Ⅱ)用前一个实验结束后的残留固体与乙醇蒸气反应(该残留固体可使乙醇发生去氢氧化),并检验反应产物。(已知乙醇的沸点为78℃)
(1)见图中已装配好一套装置,回答下列问题:
①该装置用于进行实验(选填Ⅰ或Ⅱ) ,需加热的仪器有(选填序号字母) ;
②在试管D中所放试剂及可观察到的现象是
,
反应的离子方程式为 ;
③为确保反应物有较高的利用率,且使装置中气流平稳,应对C部分进行的改进是 ;
(2)用图中其它仪器组装完成另一实验的装置,回答以下问题:
①这些仪器按气流从左到右方向的连接顺序是(填写序号字母) → → →H;其中H的作用是 ;
②组装试管F时,试管口应略向下倾斜,其原因是
;
(3)若各装置中的反应都能进行完全,实验后测得A中固体质量减轻ag、E增重bg、G增重cg,则表示结晶水x值的计算式为(从a、b、c中选两个量求算,不必化简)
。
4.工业上测量SO2、N2、O2混合气体中SO2含量的装置如下图;反应管中装有碘的淀粉溶液。SO2和I2发生的反应为(N2、O2不与I2反应):SO2+I2+2H2O=H2SO4+2HI
(1)混合气体进入反应管后,量气管内增加的水的体积等于 的体积(填写气体的分子式)。
(2)反应管内溶液蓝色消失卮,没有及时停止通气,则测得的SO2含量 (选填:偏高,偏低,不受影响)。
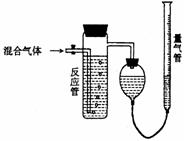 (3)反应管内的碘的淀粉溶液也可以用 代替(填写物质名称)。
(3)反应管内的碘的淀粉溶液也可以用 代替(填写物质名称)。
(4若碘溶液体积为VamL.,浓度为Cmol·L-1,N2与O2的体积为VbmL(已折算为标准状况下的体积)。用C、Va、Vb表示SO2的体积百分含量为: 。
(5)将上述装置改为简易实验装置,除导管外,还需选用的仪器为. (选下列仪器的编号)。
 a.烧杯 b.试管 c.广口瓶 d.容量瓶 e.量筒 f.单孔塞 g.双孔塞
a.烧杯 b.试管 c.广口瓶 d.容量瓶 e.量筒 f.单孔塞 g.双孔塞
3.选择使用下列仪器、药品验证由铜和适量浓硝酸反应
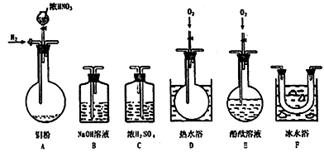
产生的气体中含有NO(N2和O2的用量可自由控制)
已知:Ⅰ NO+NO2+2OH-=2NO2-+H2O
Ⅱ气体液化温度NO2:21℃, NO:-152℃
(1)现有甲、乙、丙3位同学分别设计了以下3个实验方案(用仪器的连接顺序表示)。
甲:A→C→F→D→B 乙:A→B→C→E 丙:A→F→D→B
请回答:甲、乙、丙3位同学提出的实验方案是否能验证Cu与适量浓硝酸反应,产生的气体中含有NO(填“能”或“不能”)。
甲 ,乙 ,丙 ;
(2)反应前先通足量N2,其目的是 ;
(3)确认气体中含有NO的现象是 。
2. 实验室有CuO和Cu粉的混合物。请你利用给出的实验仪器及试剂,设计两种测定该样品(已称得其质量为m克)中氧化铜质量分数的方法,并填写表格中的有关内容。
|
实验 方法 |
实验过程中所发生反应的 化学方程式 |
实验所用仪器 (用编号表示) |
实验需直接测定的有关物理量 (用文字说明) |
|
1 |
|
|
|
|
2 |
|
|
|
实验可能用到的主要仪器:
①托盘天平 ②启普发生器 ⑧硬质玻璃管 ④泥三角 ⑤烧杯 ⑥坩埚 ⑦酒精灯 ⑧玻棒 ⑨漏斗 ⑩干燥管
实验可能用到的试剂:
a.锌粒 b.稀硫酸 c.氯化钠溶液 d,浓硫酸
1.某硝酸钠固体中混有少量硫酸铵和碳酸氢钠杂质,试设计一个实验方案,既除去杂质,又配成硝酸钠溶液。
供选用的试剂有:①稀HCl ②稀HNO3 ③稀H2SO4 ④NaOH溶液 ⑤Na2CO3溶液 ⑥BaCl2溶液 ⑦Ba(OH)2溶液 ⑧Ba(NO3)2溶液
供选用的实验操作有:A.加热 B.过滤 C.分液 D.蒸发 E.蒸馏 F.结晶
要求:试剂不超过三种,空格按要求填人试剂或操作的序号,可不填满。
实验方案:先将固体溶于蒸馏水配成溶液,然后填下列空格:
选择试剂
选择操作
2.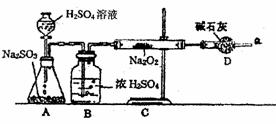 某同学通过下列装置进行实验,推断SO2与Na2O2反应的产物,已知SO2可由浓H2SO4与Na2SO3反应制取,Na2O2完全反应。
某同学通过下列装置进行实验,推断SO2与Na2O2反应的产物,已知SO2可由浓H2SO4与Na2SO3反应制取,Na2O2完全反应。
(1)怎样确定反应中是否有O2生成?
;
(2)装置B的作用是
;
装置D的作用是 ;
(3)该同学为了确定另一产物是Na2SO3还是Na2SO4,设计实验如下:
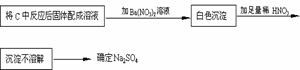
你认为该同学的实验是否合理 ,理由
。
若你认为不合理,请你设计一个合理实验来确定产物(括号内填加入物质,方框内填现象);若你认为合理,可不回答此问。

检测提高
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com