1．对于任意实数a，b定义运算a*b＝(a+1)(b+1)－1，给出以下结论：①对于任意实数a，b，c，有a*(b+c)＝(a*b)+(a*c)；②对于任意实数a，b，c，有a*(b*c)＝(a*b)*c；③对于任意实数a，有a*0＝a，则以上结论正确的是________．(写出你认为正确的结论的所有序号)

解析：按新定义，可以验证a*(b+c)≠(a*b)+(a*c)，所以①不成立；

而a*(b*c)＝(a*b)*c成立，a*0＝(a+1)(0+1)－1＝a.所以正确的结论是②③.

答案：②③

10．已知数列{a_n}的前n项的和S_n满足S_n＝2a_n－3n (n∈N^*)．

(1)求证{a_n+3}为等比数列，并求{a_n}的通项公式；

(2)数列{a_n}是否存在三项使它们按原顺序可以构成等差数列？若存在，求出一组适合条件的项；若不存在，请说明理由．

证明：(1)∵S_n＝2a_n－3n (n∈N^*)，∴a₁＝S₁＝2a₁－3，∴a₁＝3.

又由得a_n+1＝S_n+1－S_n＝2a_n+1－2a_n－3，

∴a_n+1+3＝2(a_n+3)，∴{a_n+3}是首项为a₁+3＝6，公比为2的等比数列．

∴a_n+3＝6×2^n－1，即a_n＝3(2ⁿ－1)．

(2)解答：假设数列{a_n}中存在三项a_r，a_s，a_t (r<s<t)，它们可以构成等差数列．

由(1)知a_r<a_s<a_t，则2a_s＝a_r+a_t，

∴6(2^s－1)＝3(2^r－1)+3(2^t－1)，即2^s+1＝2^r+2^t，∴2^s+1－r＝1+2^t－r(*)

∵r、s、t均为正整数且r<s<t，∴(*)左边为偶数而右边为奇数，

∴假设不成立，即数列{a_n}不存在三项使它们按原顺序可以构成等差数列．

9．如右图所示，O是正方形ABCD的中心，PO⊥底面ABCD，E是PC的中点，求证：平面PAC⊥平面BDE.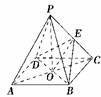

证明：∵PO⊥底面ABCD，∴PO⊥BD.

又∵O是正方形的中心，∴BD⊥AC.

∵PO∩AC＝0，∴BD⊥平面PAC，

又BD⊂平面BDE，所以平面PAC⊥平面BDE.

8．试证：当n∈N^*时，f(n)＝3²ⁿ⁺²－8n－9能被64整除．

证明：证法一：(1)当n＝1时，f(1)＝64，命题显然成立．

(2)假设当n＝k(k∈N^*，k≥1)时，f(k)＝3^2k+2－8k－9能被64整除．

当n＝k+1时，由于3^2(k+1)+2－8(k+1)－9

＝9(3^2k+2－8k－9)+9·8k+9·9－8(k+1)－9＝9(3^2k+2－8k－9)+64(k+1)，

即f(k+1)＝9f(k)+64(k+1)，∴n＝k+1时命题也成立．

根据(1)、(2)可知，对于任意n∈N^*，命题都成立．

证法二：(1)当n＝1时f(1)＝64

命题显然成立．

(2)假设当n＝k(k∈N^*，k≥1)时，f(k)＝3^2k+2－8k－9能被64整除．

由归纳假设，设3^2k+2－8k－9＝64m(m为大于1的自然数)，

将3^2k+2＝64m+8k+9代入到f(k+1)中得

f(k+1)＝9(64m+8k+9)－8(k+1)－9＝64(9m+k+1)，∴n＝k+1时命题也成立．

根据(1)(2)知，对于任意n∈N^*，命题都成立．

7．如下图，在杨辉三角形中，从上往下数共有n(n∈N^?)行，在这些数中非1的数字之和是________________．

1

1　1

1　2　1

1　3　3　1

1　4　6　4　1

……

解析：所有数字之和S_n＝2⁰+2+2²+…+2^n－1＝2ⁿ－1，除掉1的和2ⁿ－1－(2n－1)＝2ⁿ－2n.

答案：2ⁿ－2n

6．如果函数f(x)的定义域为R，对于m，n∈R，恒有f(m+n)＝f(m)+f(n)－6，且f(－1)是不小于5的正整数，当x>1时，f(x)<0.那么具有这种性质的函数f(x)＝________.(注：填上你认为正确的一个函数即可)

解析：令m＝n＝0，由f(m+n)＝f(m)+f(n)－6得f(0)＝6，设f(x)＝ax+6，

∵f(－1)＝－a+6≥5.∴a≤1.

又知当x>1时，f(x)<0，∴a<0且f(1)＝a+6≤0.

∴a≤－6 (a∈Z)．∴a＝－6，－7，－8…都符合要求．

答案：－7x+6

5．已知函数f(x)＝ax+2a+1，当x∈[－1,1]时，f(x)有正值也有负值，则实数a的取值范围为________．

解析：由题意得f(x)＝ax+2a+1为斜率不为0的直线，由单调性知f(1)·f(－1)<0，

∴(a+2a+1)·(2a－a+1)<0.∴－1<a<－.

答案：－1<a<－

4．设a、b、c是互不相等的正数，则下列不等式中不恒成立的是(　)

A．|a－b|≤|a－c|+|b－c|　 　　　　 B．a²+≥a+

C．|a－b|+≥2　 　　　　　　　　 D.－＜－

解析：A：|a－b|＝|(a－c)+(c－b)|≤|a－c|+|c－b|一定成立．

B：a²+＝²－2，a²+≥a+⇔²≥+2

⇔²－－2≥0⇔a+≥2或a+≤－1.

而a+≥2或a+≤－2.∴上式恒成立．

C：|a－b|≥0，而a－b∈R，∴不能使用均值不等式．

D：显然成立．

答案：C

3．设S是至少含有两个元素的集合．在S上定义了一个二元运算“*”(即对任意的a，b∈S，对于有序元素对(a，b)，在S中有唯一确定的元素a*b与之对应)．若对任意的a，b∈S，有a*(b*a)＝b，则对任意的a，b∈S，下列等式中不恒成立的是(　)

A．(a*b)*a＝a　 　　　B．[a*(b*a)]*(a*b)＝a

C．b*(b*b)＝b　 　　　D．(a*b)*[b*(a*b)]＝b

解析：此题只有一个已知条件：a*(b*a)＝b.B中a*(b*a)＝b原式变为b*(a*b)＝a，成立，C中相当于已知条件中a替换为b，明显成立，D中，b*(a*b)＝a，原式变为(a*b)*a＝b成立．

答案：A

2．下列条件：①ab>0，②ab<0，③a>0，b>0，④a<0，b<0，其中能使+≥2成立的条件有(　)

A．1个　 　　B．2个　 　　C．3个　 　　D．4个

解析：要使+≥2，只要>0且>0，即a，b不为0且同号即可，故有3个．

答案：C