7.(2010福建文)

5.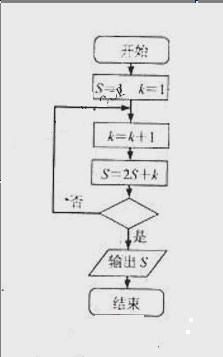(2010浙江文)4.某程序框图所示，若输出的S=57，则判断框内为

(A) k>4?　　　　　　　 　　 　　 (B) k>5?

(C) k>6?　　　　　 　　　 　　(D) k>7?　　

[答案]A

解析：本题主要考察了程序框图的结构，以及与数列有

关的简单运算，属容易题

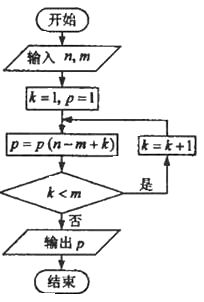
4.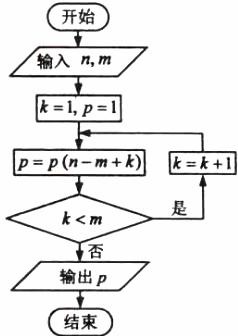(2010辽宁理)(4)如果执行右面的程序框图，输入正整数n，m，满足n≥m，那么输出的P等于

(A)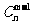　　

(B)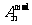 　　

(C)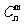 　　

(D)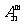

[答案]D

[命题立意]本题考查了循环结构的程序框图、排列公式，考查了学生的视图能力以及观察、推理的能力

[解析]第一次循环：k=1,p=1,p=n-m+1;

　　　　 第二次循环：k=2,p=(n-m+1)(n-m+2)；

　　　　 第三次循环：k=3，p=(n-m+1) (n-m+2) (n-m+3)

　　　　 ……

第m次循环：k=3，p=(n-m+1) (n-m+2) (n-m+3)…(n-1)n

　　　　 此时结束循环，输出p=(n-m+1) (n-m+2) (n-m+3)…(n-1)n=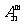

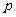3.(2010辽宁文)(5)如果执行右面的程序框图，输入，那么输出的等于

(A)720　　　

　(B) 360　　

　 (C) 240　　　

　(D) 120

[答案]B

解析：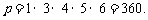

2.(2010陕西文)5.右图是求x₁,x₂，…，x₁₀的乘积S的程序框图，图中空白框中应填入的内容为　　 (A)S=S*(n+1)

(B)S=S*x_n+1

(C)S=S*n

(D)S=S*x_n

[答案]D

解析：本题考查算法

S=S*x_n

1.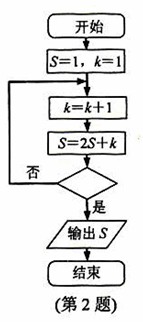(2010浙江理)(2)某程序框图如图所示，

若输出的S=57，则判断框内位　　　

(A) k＞4?　　　　　　　　　　

(B)k＞5?　

(C) k＞6?　　　　　　　　　　

(D)k＞7?　

[答案]A

解析：本题主要考察了程序框图的结构，

以及与数列有关的简

单运算，属容易题

2010年高考题

3．已知函数f(x)＝x³+ax+b定义在区间[－1,1]上，且f(0)＝f(1)，设x₁，x₂∈[－1,1]且x₁≠x₂.

(1)求证：|f(x₁)－f(x₂)|<2|x₁－x₂|；

(2)若0<x₁<x₂≤1，求证：|f(x₁)－f(x₂)|<1.

证明：(1)由f(0)＝f(1)，得b＝1+a+b，解得a＝－1.故f(x)＝x³－x+b，设x₁，x₂∈[－1,1]．

则|f(x₁)－f(x₂)|＝|x－x₁－x+x₂|＝|x₁－x₂|·|x+x₁x₂+x－1|.

因为－1≤x₁，x₂≤1，则0≤x≤1,0≤x≤1，－1≤x₁x₂≤1，所以－1≤x+x+x₁x₂≤3，

当且仅当x₁＝x₂＝±1时，右边取等号．∵x₁≠x₂，∴右边等号取不到．

若x+x+x₁x₂＝－1，则x+x+(x₁x₂+1)＝0.

∵x₁x₂+1≥0，∴x₁＝x₂＝0且x₁x₂+1＝0矛盾，∴左边等号也取不到．

所以两边等号均不成立．所以－1<x+x+x₁x₂<3.

所以－2<x+x+x₁x₂－1<2.所以|x+x+x₁x₂－1|<2，

即|f(x₁)－f(x₂)|<2|x₁－x₂|.

(2)因为f′(x)＝3x²－1，令f′(x)＝0，则x＝.由导数的知识容易验证，

当x＝时，[f(x)]_min＝b－.又f(1)＝b，所以当x∈(0,1]时，b－≤f(x)≤b.

则b－≤f(x₁)≤b，b－≤f(x₂)≤b.因为x₁≠x₂，所以f(x₁)≠f(x₂)．所以－≤f(x₁)－f(x₂)≤.即|f(x₁)－f(x₂)|≤.又<1，所以|f(x₁)－f(x₂)|<1.

2．已知数列{a_n}的各项都是正数，且满足：a₀＝1，a_n+1＝a_n·(4－a_n)(n∈N)．

证明：a_n<a_n+1<2(n∈N)．

证明：证法一：用数学归纳法证明：

(1)当n＝0时，a₀＝1，a₁＝a₀(4－a₀)＝，所以a₀<a₁<2，命题正确．

(2)假设n＝k－1(k∈N^*)时命题成立，即a_k－1<a_k<2.

则当n＝k时，a_k－a_k+1

＝a_k－1(4－a_k－1)－a_k(4－a_k)＝2(a_k－1－a_k)－(a_k－1－a_k)(a_k－1+a_k)

＝(a_k－1－a_k)(4－a_k－1－a_k)．

而a_k－1－a_k<0,4－a_k－1－a_k>0，所以a_k－a_k+1<0.

又a_k+1＝a_k(4－a_k)＝ [4－(a_k－2)²]<2.所以n＝k时命题成立．

由(1)(2)可知，对一切n∈N时有a_n<a_n+1<2.

证法二：用数学归纳法证明：

(1)当n＝0时，a₀＝1，a₁＝a₀(4－a₀)＝，所以0<a₀<a₁<2；

(2)假设n＝k－1(k∈N^*)时有a_k－1<a_k<2成立，令f(x)＝x(4－x)，f(x)在[0,2]上单调递增，所以由假设有：f(a_k－1)<f(a_k)<f(2)，

即a_k－1(4－a_k－1)<a_k(4－a_k)<×2×(4－2)，

也即当n＝k时，a_k<a_k+1<2成立．所以对一切n∈N，有a_k<a_k+1<2.