216.在正方体木块ABCD－A₁B₁C₁D₁的表面上有一动点P由顶点A出发按下列规则向点C₁移动； ⑴点P只能沿着正方体木块的棱或表面对角线移动； ⑵点P每一变化位置，都使P点到C₁点的距离缩短。 动点P共有_________种不同的运行路线。 解析：通过画图逐一计数，共得12种不同路线(从B到C₁，就有3种不同路线)

经过一条边，一条对角线的情况有6种， ，，

，，

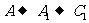经过三条边的情况有6种：

，，

，，

215. 如图2－22：在长方体AC₁中， (1)求证：BC₁//平行平面AB₁D₁ (2)若E、F分别是D₁C，BD的中点，则EF//ADD₁A₁ 解析：(1)∵D₁C₁DCAB ∴ABC₁D₁是平行四边形 BC₁//AD₁ 又BC₁平面AB₁D₁，又AD₁平面AB₁D₁

BC₁//平面AB₁D₁ (2)证明：连结AF、CF、AD₁， ∵ABCD是正方形，且F是BD的中点，知A、F、C三点共线， 且F是AC的中点，又E是CD₁的中点 ∴EF//AD，又EF平面ADD₁A₁，AD平面ADD₁A₁， ∴EF//平面ADD₁A₁

214. 直线a//直线b，直线a与平面α相交，判定直线b与平面α的位置关系，并证明你的结论

　证明：假设直线b与α不相交，则bα或b//α (1)若bα，由a//b，bα，aαa//α，与a与平面α相交矛盾，故bα不可能。 (2)若b//α，又a// b，a，b可以确定平面β，设α∩β＝c，由cα,知b与c没有公共点，又b、c同在平面β内，故b//c，又a//b，故a//c，cα，aαa//α，这与a与平面α相交矛盾。故b不平行α。 综上所述，b与α必相交。

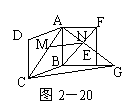
212.如图2－20，两个全等的正方形ABCD和ABEF所在平面相交于AB，M∈AC，N∈FB，且AM＝FN，求证：MN//平面BCE。

解析： 要证MN//平面BCE，就是要在平面BCE上找一条直线，证明它与MN平行即可。

证明: 连结AN并延长，交BE延长张于G，连结CG。 由AF//BG，知，故MN//CG，MN平面BCE，CG平面BCE，于是MN//平面BCE。

点评:证线面平行，通常转化为证线线平行，关键是在平面内找到所需的线。 213. 如图2－21，正方体ABCD－A₁B₁C₁D₁的棱长为2，E为DD₁的中点， (1)判断BD₁和过A、C、E三点的平面的位置关系， 　并证明你的结论。 (2)求ACE的面积。 证明(1)：连结BD，令BD∩AC＝F。 ∵BD₁和过A、C、E三点的平面平行， 则F是DB的中点，又E是DD₁的中点， ∴EF∥BD₁ 又EF平面ACE，BD₁平面ACE， ∴BD₁∥平面ACE (2)在正方形ABCD中，AB＝2，AC＝2，∴AF＝ 在直角△ADE中，AD＝2，DE＝1，∴AE＝

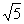
在Rt△EAF中，EF＝＝＝ ∴

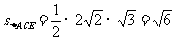
211. 下列说法中正确的是(　)： A. 直线l平行于平面α内的无数条直线，则l//α B. 若直线a在平面α外，则a//α C. 若直线a//b，直线bα，则a//α D. 若直线a//b，bα，那么a就平行于平面α内的无数条直线

解析：画出图形，根据直线与平面平行的定义和判定定理进行分析。

解答: 由直线l 虽与平面α内无数条直线平行，但l有可能在平面α内，知l不一定平行于α，从而排除A 直线a在平面α外，包括两种情况：a//α或a与α相交，故a与α不一定平行，从而排除B 直线a//b ，bα只能说明a和b无公共点，但a可能在平面α内，故a不一定平行于α，从而排除C a//b，bα，那么aα或a//α，故a可能与平面α内的无数条直线平行，从而选择D

点评: 判定直线与平面平行时，要注意直线与平面平行的判定定理中的三个条件，缺一不可。　　　　 。

21．(本小题满分13分)

　　　 已知椭圆的离心率为，其左、右焦点分别为F₁、F₂，点P是坐标平面内一点，且(O为坐标原点)。

　 (1)求椭圆C的方程；

　 (2)过点且斜率为的动直线交椭圆于A、B两点，在轴上是否存在定点M，使以AB为直径的圆恒过这个点？若存在，求出M的坐标和面积的最大值；若不存在，说明理由。

20．(本小题满分13分)

　　　 已知数列满足，点在直线上，数列满足

　 (1)求的值；

　 (2)求证：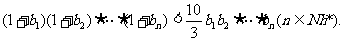

19．(本小题满分13分)

　　　 张家界某景区为提高经济效益，现对某一景点进行改造升级，从而扩大内需，提高旅游增加值，经过市场调查，旅游增加值万元与投入万元之间满足：为常数。当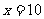万元时，万元；当万元时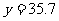，万元。(参考数据：)

　 (1)求的解析式；

　 (2)求该景点改造升级后旅游利润的最大值。(利润=旅游增加值-投入)

18．(本小题满分12分)

　　　 下图分别为三棱锥S-ABC的直观图与三视图，在直观图中，，M、N分别为AB、SB的中点。

　 (1)求证：；

　 (2)求二面角M-NC-B的余弦值。

17．(本小题满分12分)

　　　 “上海世博会”于2010年5月1日至10月31日在上海举行，世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所，陈列其中的艺术品是体现兼容并蓄，海纳百川的重要文化载体，为此，上海世博会事物协调局举办“中国2010年上海世博会”中国馆·贵宾厅艺术品方案征集活动，某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应证，假设代表中有中国画、书法、油画入选“中国馆·贵宾厅”的概率均为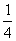，陶艺入选“中国馆·贵宾厅”的概率为。

　 (1)求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率；

　 (2)设该地美术馆选送的四件代表作中入选“中国馆·贵宾厅”的作品件数为随机变量，求的数学期望。