3．体会分类、转化等数学思想.

[课后作业]

班级　　 姓名　　　　　 学号　　　

2．圆周角定义、圆周角定理，会用定理进行推证和计算。

1. 探索了圆周角的有关性质

2. 如图， A、B、E、C四点都在⊙O上，AD是△ABC的高，∠CAD

=∠EAB,AE是⊙O的直径吗？为什么？

1.如左图，△ABC的顶点都在⊙O上，AD是△ABC的高，AE是⊙O的直径.

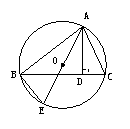
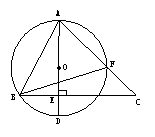△ABE与△ACD相似吗？为什么？

变式：如右图，△ABF与△ACB相似吗？

4.　　 巩固练习

3.　　 典型例题

例1.AB是☉O直径，弦CD与AB相交于点E，∠ACD=60⁰，∠ADC=50⁰，

求∠CEB的度数.

例2．如图AB是⊙O的直径，弦CD与AB相交于点E，∠ACD=60°，∠ADC=50°,求∠CEB的度数.

例3.在ΔABC的3个顶点都在☉O上，AD是ΔABC的高，AE是☉O的直径，求证：ΔABE∽ΔACD。

2.　　 总结

直径所对的圆周角是　　 角，90⁰的圆周角所对的弦是　　 。

1.　　 尝试、交流

(1)BC是☉O的直径，它所对的圆周角是锐角、还是钝角、还是直角？为么？

(2)圆周角∠BAC=90⁰，弦BC过圆心吗？为什么？

问题情境：我们学过哪些与圆有关的角？它们之间有什么关系？