1．下列词语中加点的字，读音全都不相同的一组是

A．模棱　　 摹拟　　 落寞 　　莫逆之交　　 顶礼膜拜

B．扉页　　 菲薄　　 斐然　　 匪夷所思　　 蜚短流长

C．诋毁　　 底蕴　　 邸所　　 低首下心　　 砥柱中流

D．搁浅　　 奶酪　　 贿赂　　 洛阳纸贵　　 一丘之貉

10、已知函数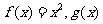为一次函数，且一次项系数大于零，若的表达式。

解：由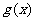为一次函数，设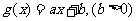

∵

∴,

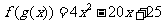
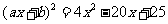即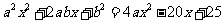

解得a＝2,b＝-5

故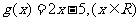

[探索题]

设f(x)是一次函数,当x≥0时,恒有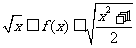,求f(x)的函数解析式.

解: 设,当x=1时,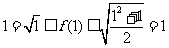即f(1)=1.

∴a+b=1,b=1-a

∵对一切x≥0,恒有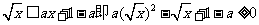,显然a>0,

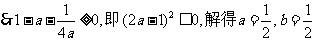
此时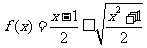恒成立,故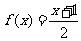

9、用长为l的铁丝弯成下部为矩形，上部为半圆形的框架(如下图)，若矩形底边长为2x，求此框架围成的面积y与x的函数关系式，并写出其定义域.

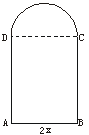
解：∵AB=2x，则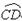=πx，AD=.

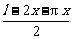∴y=2x·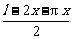+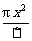=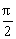－(+2)x²+lx.

由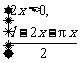＞0，解得0＜x＜.

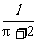8、解：∵f(a)∈N，f(b)∈N，f(c)∈N，且f(a)+f(b)+f(c)=0，

∴有0+0+0=0+1+(－1)=0.

当f(a)=f(b)=f(c)=0时，只有一个映射；

当f(a)、f(b)、f(c)中恰有一个为0，而另两个分别为1，－1时，有C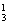·A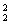=6个映射.因此所求的映射的个数为1+6=7.

评述：本题考查了映射的概念和分类讨论的思想.

8、集合M={a，b，c}，N={－1，0，1}，映射f:M→N满足f(a)+f(b)+f(c)=0，那么映射f:M→N的个数是多少？

7、解：∵f(1)=3×1+1=4，f(2)=3×2+1=7，f(3)=3×3+1=10，f(k)=3k+1，由映射的定义知

(1)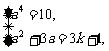或(2)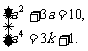 　

∵a∈N，∴方程组(1)无解.

解方程组(2)，得a=2或a=－5(舍)，3k+1=16，3k=15，k=5.∴A={1，2，3，5}，B={4，7，10，16}.

7、若f :y=3x+1是从集合A={1，2，3，k}到集合B={4，7，a⁴，a²+3a}的一个映射，求自然数a、k的值及集合A、B.

5、(2004年湖北，3)已知f(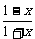)=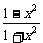，则f(x)=　　　 　

6 (2004北京)函数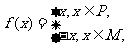其中P、M为实数集R的两个非空子集，又规定f(P)={y|y=f(x),x∈P}，f(M)={y|y=f(x),x∈M}，，给出下列四个判断：

　 ①若P∩M=φ,则f(P)∩f(M)=φ　

②若P∩M≠φ,则f(P)∩f(M)≠φ　

　 ③若P∪M=R,则f(P)∪f(M)=R　

④若P∪M≠R,则f(P)∪f(M)≠R

　其中正确判断的序号是　　　　　

简答:1-4、BCD； 4. 3,2,1;　 　5、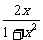； 6、②④.提示:若P∩M≠φ则只有若P∩M={0}这一种可能．否则f(x)不是单值，与函数定义矛盾。②和④是正确的．

[解答题]

4、已知两个函数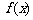和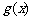的定义域和值域都是集合{1,2,3},其定义如下表.

则g(f(1))_、g(f(2))、g(f(3))的值依次为　　　　

3、(2006浙江10)函数f：{1，2，3}{1，2，3} 满足f(f(x))＝f(x)，则这样的函数个数共有　　 (　 )

(A)1个　　　 (B)4个　　　 (C)8个　　　 (D)10个

[填空题]