4．质量为25.6g的KOH和KHCO₃混合物在250^oC的密闭容器中充分煅烧后排出气体，冷却，残留固体20.7g，原混合物中KOH和KHCO₃的物质的量关系正确的是

A．大于　 　　B．小于 　　C．等于 　　D．任意比

(此题以KOH和KHCO₃的性质为依托，考查学生运用反应方程式计算的能力。可运用假设法答题。)

3．等体积、等物质的量浓度的硫酸、氢氧化钠溶液分别放在甲、乙两烧杯中，各加等质量的铝，生成氢气的体积比为5：6，则甲、乙两烧杯中的反应情况可能分别是( 　)

A．甲、乙中都是铝过量

B．甲中铝过量、乙中碱过量

C．甲中酸过量、乙中铝过量

D．甲中酸过量、乙中碱过量

(该题考查有关化学方程式的计算，同时考查学生思维的逻辑性、敏捷性，能力要求较高。解题依据判断物质过量的方法，计算出以后通过比较、推理可求得。)

2．用足量的CO还原48.0g某种氧化物，将生成的气体通入足量澄清石灰水中，得到60.0g沉淀，则该氧化物是( 　)

A．FeO　　　　　 B．Fe₂O₃ C．CuO　　 D．Cu₂O

(本题以氧化还原反应、沉淀反应为依托，考查学生对氧化还原反应中基本概念的理解，同时考查学生的逆向思维能力、灵活处理问题的能力和综合计算能力。答题时利用选项的暗示及质量关系，或通过比较求解。)

1．加热碳酸镁和氧化镁的混合物mg，使之完全反应，得剩余物ng，则原混合物中氧化镁的百分含量为( 　)

A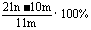．　　 　B． 　　

C．　　 　　D．

(该题旨在考查学生运用差量法进行计算。答题时由反应前后物质质量差量关系列式计算。)

2．(2000年上海高考题)某天然碱(纯净物)可看作由CO₂和NaOH反应后的产物所组成。称取天然碱样品四份，溶于水后，分别逐滴加入相同浓度的盐酸溶液30mL，产生CO₂的体积(标准状况)如下表：

(1)由第Ⅰ组数据中的CO₂体积与样品质量之比，可以推测用2.49g样品进行同样的实验时，产生CO₂_________mL(标准状况)。

(2)另取3.32g天然碱样品于300℃加热分解至完全(300℃时Na₂CO₃不分解)，产生CO₂112mL(标准状况)和水0.45g，计算并确定该天然碱的化学式。　

(3)已知Na₂CO₃和HCl(aq)的反应分下列两步进行：

Na₂CO₃+HCl→NaCl+NaHCO₃

NaHCO₃+HCl→NaCl+CO₂↑+H₂O

由上表中第Ⅳ组数据可以确定所用的HCl(aq)的浓度为

　 　　　mol/L。

(4)依据上表所列数据以及天然碱的化学式，讨论并确定上述实验中CO₂(标准状况)体积V(mL)与样品质量W(g)之间的关系式。

(该题以天然碱的组成及碳酸盐的性质为依托，构筑成一道有层次、有深度且思维容量大的综合计算题。对信息的理解能力、对数据的观察和处理能力、综合计算能力是完成本题的关键。)

新活题网站

1．(2001年全国高考题)标准状况下1.68 L无色可燃气体在足量氧气中完全燃烧。若将产物通入足量澄清石灰水，得到的白色沉淀质量为15.0 g；若用足量碱石灰吸收燃烧产物，增重9.3 g。

(1)计算燃烧产物中水的质量。

(2)若原气体是单一气体，通过计算推断它的分子式。

(3)若原气体是两种等物质的量的气体的混合物，其中只有一种是烃，请写出它们的分子式(只要求写出一组)。

(此题是一道综合性的化学计算推理题，意在考查学生的综合计算能力、归纳分析能力和判断推理能力。答题时抓住物质的性质，利用化学方程式所体现的量的关系来确定分子组成，根据第③问的题干要求，运用平均组成法作出合理的判断。)

4．借助数学工具解决化学问题的综合运用。化学计算能力以化学知识和技能为载体，测试考生将化学问题抽象成数学问题，利用数学工具，通过计算和推理，解决化学问题的能力。主要包括数轴的借用、函数的思想、讨论的方法、空间想象的能力、不等式的迁移及实验数据(表格、图象)的分析等多方面的知识。该类题目的解题思路是：运用所掌握的数学知识，通过分析化学变量之间的相互关系，建立一定的数学关系(等式、不等式、函数、几何模型、图像关系、数列、数轴)用以解题，这是高层次的素质教育的体现，也是学科能力的体现。

典型题点击

3．讨论型的综合计算包括过量计算讨论、过程讨论、不定方程讨论，他们都可归结为范围讨论计算，此类题融化学原理、元素化合物知识、数据分析、逻辑推理于化学计算之中，技巧性强，方法灵活，因而是高考的热点和难点。范围讨论计算所依据的化学原理是反应物之间相对含量或浓度不同而产物不同(如NaOH与CO₂反应、Na₂O₂与NaHCO₃共热、Cu与HNO₃反应、FeO与C反应等)，所以，此类题实际上是过量计算的演化和延伸。解题方法思路是：

(1)写方程式、找完全点。即写出因反应物相对量不同而可以发生的化学反应方程式，并分别计算找出二者恰好完全反应时的特殊点。

(2)确定范围、计算判断。即以恰好完全反应的点为基准，讨论大于、小于或等于的情况，从而划出相应的区间，确定不同范围，进行相对过量计算即可。

2．假设法的综合计算包括极端假设、过程假设、赋值假设等。其中极端假设思想运用较多，采取极端假设可把问题或过程推向极限，使复杂的问题变得单一化、极端化和简单化，通过对极端问题的讨论，使思路清晰，过程简明，从而迅速准确地得到正确答案。常用于混合物的计算、化学平衡、平行反应等。

1．利用化学方程式、关系式的综合计算：此类计算可能涉及到许多反应，存在多种变化关系，关键是抓住始态和终态，写出关系式(一般采用物质的量之比)，一次列式求解，而不必对每一步反应都进行计算。正确提取关系式是用关系式法解题的关键，提取关系式的常用方法有：

①从化学方程式中提取关系式；

②从化学式和电极反应式等中提取关系式；

③从物质和对应的差量(质量差、体积差、物质的量差、浓度差等)之间提取关系式。

也可依据反应过程中某一元素的存在形式，结合二元代数方程，运用守恒法(如质量守恒、元素守恒、电荷守恒、得失电子守恒等)列出关系解题。