
4.由简单命题和逻辑联结词“或”、“且”、“非”构成的命题是复合命题
3.不含有逻辑联结词的命题是简单命题;
2.逻辑符号:
“或”的符号是“∨”,例如“P或q”可以记作“P ∨q”;
“且”的符号是“∧”,例如,“P且q”可以记作“P∧q”;
“非”的符号是“┑”,例如,“非P”可以记作“┑P”.
1.“或”、“且”、“非”这些词叫做逻辑联结词;
3.复合命题的构成形式
如果用 p, q, r, s……表示命题,则复合命题的形式接触过的有以下三种:
即:p或q 记作 pÚq p且q 记作 pÙq
非p (命题的否定) 记作 Øp
释义:“p或q”是指p,q中的任何一个或两者.例如,“x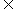 A或x
A或x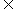 B”,是指x可能属于A但不属于B(这里的“但”等价于“且”),x也可能不属于A但属于B,x还可能既属于A又属于B(即x
B”,是指x可能属于A但不属于B(这里的“但”等价于“且”),x也可能不属于A但属于B,x还可能既属于A又属于B(即x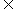 A3B);又如在“p真或q真”中,可能只有p真,也可能只有q真,还可能p,q都为真.
A3B);又如在“p真或q真”中,可能只有p真,也可能只有q真,还可能p,q都为真.
“p且q”是指p,q中的两者.例如,“x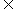 A且x
A且x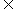 B”,是指x属于A,同时x也属于B(即x
B”,是指x属于A,同时x也属于B(即x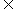 A
A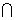 B).
B).
“非p”是指p的否定,即不是p. 例如,p是“x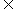 A”,则“非p”表示x不是集合A的元素(即x
A”,则“非p”表示x不是集合A的元素(即x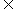
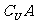 ).
).
开语句:语句中含有变量x或y,在没有给定这些变量的值之前,是无法确定语句真假的.这种含有变量的语句叫做开语句(有的逻辑书也称之为条件命题).也可以把简单的开语句用逻辑联结词“或”、“且”、“非”连结起来,构成复合的开语句(有的逻辑书也称之为复合条件命题),这里的“或”、“且”、“非”与复合命题中的“或”、“且”、“非”符号与意义相同.在进行命题教学时,要注意命题与开语句的区别,特别在举有关逻辑联结词“或”、“且”、“非”的例子时,容易把两者混淆.
例1(课本第26页例1)分别指出下列复合命题的形式及构成它们的简单命题:
⑴ 24既是8的倍数,也是6的被数;
⑵ 李强是篮球运动员或跳高运动员;
⑶ 平行线不相交.
解:⑴ 这个命题是p且q的形式,其中p:24是8的倍数,q:24是6的倍数.
⑵ 这个命题是p或q的形式,其中p:李强是篮球运动员,q:李强是跳高运动员.
⑶ 这个命题是非p的形式,其中p:平行线相交.
例2 命题“方程|x|=1的解是x=±1”中,使用逻辑联结词的情况是( )
A:使用了逻辑联结词“或” B:使用了逻辑联结词“且”
C:使用了逻辑联结词“非” D:没有使用逻辑联结词
2.简单命题与复合命题:
简单命题:不含有逻辑联结词的命题叫做简单命题
复合命题:由简单命题再加上一些逻辑联结词构成的命题叫复合命题
其实,有些概念前面已遇到过
如:或:不等式  -x-6>0的解集 { x | x<-2或x>3 }
-x-6>0的解集 { x | x<-2或x>3 }
且:不等式 -x-6<0的解集 { x | -2< x<3 } 即 { x | x>-2且x<3 }
-x-6<0的解集 { x | -2< x<3 } 即 { x | x>-2且x<3 }
1.逻辑连接词
例 ⑥ 10可以被2或5整除; (10可以被2整除或10可以被5整除)
⑦ 菱形的对角线互相垂直且平分;
(菱形的对角线互相垂直且菱形的对角线互相平分)
⑧ 0.5非整数 .( 非“0.5是整数”)
逻辑联结词:“或”、“且”、“非”这些词叫做逻辑联结词
命题的概念:可以判断真假的语句叫命题正确的叫真命题,错误的叫假命题
例如:①11>5 ②3是15的约数 ③0.7是整数
①②是真命题,③是假命题
反例:④3是15的约数吗? ⑤ x>8
都不是命题,不涉及真假(问题) 无法判断真假
“这是一棵大树”; “x<2”. 都不能叫命题.由于“大树”没有界定,就不能判断“这是一棵大树”的真假.由于x是未知数,也不能判断“x<2”是否成立.
注意:①初中教材中命题的定义是:判断一件事情的句子叫做命题;这里的定义是:可以判断真假的语句叫做命题.说法不同,实质是一样的
②判断命题的关键在于能不能判断其真假,即能不能判断其是否成立;不能判断真假的语句,就不是命题.
③与命题相关的概念是开语句例如,x<2,x-5=3,(x+y)(x-y)=0.这些语句中含有变量x或y,在没有给定这些变量的值之前,是无法确定语句真假的.这种含有变量的语句叫做开语句(有的逻辑书也称之为条件命题).
在教学时,不要在判断一个语句是不是命题上下功夫,因为这个工作过于复杂,要求学生能够从正面的例子了解命题的概念就可以了.
12. 解:(Ⅰ)假设∥,则2cosx(cosx+sinx)-sinx(cosx-sinx)=0,
∴2cos2x+sinxcosx+sin2x=0,2·+sin2x+=0,即sin2x+cos2x=-3,
∴(sin2x+)=-3,与|(sin2x+)|≤矛盾,故向量与向量不可能平行.
(Ⅱ)∵f(x)=·=(cosx+sinx)·(cosx-sinx)+sinx·2cosx=cos2x-sin2x+2sinxcosx=cos2x+sin2x=(cos2x+sin2x)=(sin2x+),
∵-≤x≤,∴-≤2x+≤,∴当2x+=,即x=时,f(x)有最大值;
当2x+=-,即x=-时,f(x)有最小值-1.
11. 解:(I) ,
,
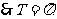 ……………3分
……………3分
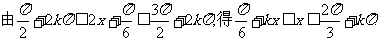
故函数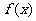 的单调递减区间是
的单调递减区间是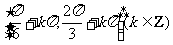 .
………6分
.
………6分
(II)
当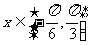 时,原函数的最大值与最小值的和
时,原函数的最大值与最小值的和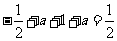 ,
,
解得a=0 . ………8分
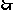
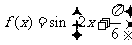 ,图象如图. ………………12分
,图象如图. ………………12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com