
3.命题“"xÎR,x2-x+3>0”的否定是
2.有这样一段演绎推理是这样的“有 些有理数是分数,整数是有理数,则整数是分数”结论显然是错误的,是因为( )
些有理数是分数,整数是有理数,则整数是分数”结论显然是错误的,是因为( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
1.命题p:存在实数m,使方程x2+mx+1=0有实数根,则“非p”形式的命题是( )
A.存在实数m,使得方程x2+mx+1=0无实根;
B.不存在实数m,使得方程x2+mx+1=0有实根;
C.对任意的实数m,使得方程x2+mx+1=0 有实根;
有实根;
D.至多有一个实数m,使得方程x2+mx+1=0有实根;
在教学中,务必理清各类型命题形式结构、性质关系,才能真正准确地完整地表达出命题的否定,才能避犯逻辑性错误,才能更好把逻辑知识负载于其它知识之上,达到培养和发展学生的逻辑思维能力。
3. 原命题“若P则q” 的形式,它的非命题“若p,则Øq”;而它的否命题为 “若┓p,则┓q”,既否定条件又否定结论。
例1 写出下列全称命题的否定:
(1)p:所有人都晨练;
(2)p:"xÎR,x2+x+1>0;
(3)p:平行四边形的对边相等;
(4)p:$ x∈R,x2-x+1=0;
分析:(1)Ø P:有的人不晨练;(2)$ x ∈R,x2+x+1≤0;(3)存在平行四边形,它的的对边不相等;(4)"xÎR,x2-x+1≠0;
∈R,x2+x+1≤0;(3)存在平行四边形,它的的对边不相等;(4)"xÎR,x2-x+1≠0;
例2 写出下列命题的否定。
(1) 所有自然数的平方是正数。
(2) 任何实数x都是方程5x-12=0的根。
(3) 对任意实数x, 存在实数y,使x+y>0.
存在实数y,使x+y>0.
(4) 有些质数是奇数。
解:(1)的否定:有些自然数的平方不是正数。
(2)的否定:存在实数x不是方程5x-1 2=0的根。
2=0的根。
(3)的否定:存在实数x,对所有实数y,有x+y≤0。
(4)的否定:所有的质数都不是奇数。
解题中会遇到省略了“所有,任何,任意”等量词的简化形式,如“若x>3,则x2>9”。在求解中极易误当为简单命题处理;这种情形下时应先将命题写成完整形式,再依据法则来写出其否定形式。
例3 写出下列命题的否定。
(1) 若x2>4 则x>2.。
(2) 若m≥0,则x2+x-m=0有实数根。
(3) 可以被5整除的整数,末位是0。
(4) 被8整除的数能被4整除。
(5) 若一个四边形是正方形,则它的四条边相等。
解(1)否定:存在实数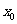 ,虽然满足
,虽然满足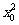 >4,但
>4,但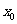 ≤2。或者说:存在小于或等于2的数
≤2。或者说:存在小于或等于2的数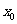 ,满足
,满足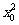 >4。(完整表达为对任意的实数x, 若x2>4 则x>2)
>4。(完整表达为对任意的实数x, 若x2>4 则x>2)
(2)否定:虽然实数m≥0,但存在一个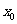 ,使
,使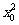 +
+ 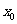 -m=0无实数根。
-m=0无实数根。 (原意表达:对任意实数m,若m≥0,则x2+x-m=0有实数根。)
(原意表达:对任意实数m,若m≥0,则x2+x-m=0有实数根。)
(3)否定:存在一个可以被5整除的整数,其末位不是0。
(4)否定:存在一个数能被8整除,但不能被4整除.(原意表达为所有能被8整除的数都能被4整除)
(5)否定:存在一个四边形,虽然它是正方形,但四条边中至少有两条不相等。(原意表达为无论哪个四边形,若它是正方形,则它的四条边中任何两条都相等。)
例4 写出下列命题的非命题与否命题,并判断其真假性。
(1)p:若x>y,则5x>5y;
(2)p:若x2+x﹤2,则x2-x﹤2;
(3)p:正方形的四条边相等;
(4)p:已知a,b为实 数,若x2+ax+b≤0有非空实解集,则a2-4b≥0。
数,若x2+ax+b≤0有非空实解集,则a2-4b≥0。
解:(1)Ø P:若 x>y,则5x≤5y; 假命题
否命题:若x≤y,则5x≤5y;真命题
(2)Ø P:若x2+x﹤2,则x2-x≥2;真命题
否命题:若x2+x≥2,则x2-x≥2);假命题。
(3)Ø P:存在一个四边形,尽管它是正方形,然而四条边中至少有两条边不相等;假命题。
否命题:若一个四边形不是正方形,则它的四条边不相等。假命题。
(4)Ø P:存在两个实数a,b,虽然满足x2+ax+b≤0有非空实解集,但使a2-4b﹤0。假命题。
否命题:已知a,b为实数,若x2+ax+b≤0没有非空实解集,则a2-4b﹤0。真命题。
评注:命题的否定与否命题是完全不同的概念。其理由:
1.任何命题均有否定,无论是真命题还是假命题;而否命题仅针对命题“若P则q”提出来的。2.命题的否定(非)是原命题的矛盾命题,两者的真假性必然是一真一假,一假一真;而否命题与原命题可能是同真同假,也可能是一真一假。
2.关键量词的否定
|
词语 |
是 |
一定是 |
都是 |
大于 |
小于 |
且 |
|
词语的否定 |
不是 |
一定不是 |
不都是 |
小于或等于 |
大于或等于 |
或 |
|
词语 |
必有一个 |
至少有n个 |
至多有一个 |
 所有x成立 所有x成立 |
所有x不成立 |
|
|
词语的否定 |
一个也没有 |
至多有n-1个 |
至少有两个 |
存在一个x不成立 |
存在有一个成立 |
|
1.全称命题、存在性命题的否定
一般地,全称命题P:" xÎM,有P(x)成立;其否定命题┓P为:$x∈M,使P(x)不成立。存在性命题P:$xÎM,使P(x)成立;其否定命题┓P为:" xÎM,有P(x)不成立。
用符号语言表示:
P:"ÎM, p(x)否定为Ø P: $ÎM, Ø P(x)
P:$ÎM, p(x)否定为Ø P: "ÎM, Ø P(x)
在具体操作中就是从命题P把全称性的量词改成存在性的量词,存在性的量词改成全称性的量词,并把量词作用范围进行否定。即须遵循下面法则:否定全称得存在,否定存在得全称,否定肯定得否定,否定否定得肯定.
问题2:写出命题的否定
(1)p:$ x∈R,x2+2x+2 ≤0;
≤0;
(2)p:有的三角形是等边三角形;
(3)p:有些函数没有反函数;
(4)p:存在一个四边形,它的对角线互相垂直且平分;
分析:(1)" xÎR,x2+2x+2>0;
(2)任何三角形都不是等边三角形;
(3)任何函数都有反函数;
(4)对于所有的四边形,它的对角线不可能互相垂直或平分;
从集合的运算观点剖析: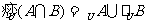 ,
,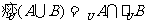
问题1:指出下列命题的形式,写出下列命题的否定。
(1)所有 的矩形都是平行四边形;
的矩形都是平行四边形;
(2)每一个素数都是奇数;
(3)"xÎR,x2-2x+1≥0
分析:(1)"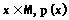 ,否定:存在一个矩形不是平行四边形;
,否定:存在一个矩形不是平行四边形;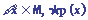
(2)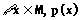 ,否定:存在一个素数不是奇数;
,否定:存在一个素数不是奇数;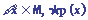
(3)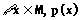 ,否定:$xÎR,x2-2x+1<0;
,否定:$xÎR,x2-2x+1<0;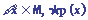
这些命题和它们的否定在形式上有什么变化?
结论:从命题形式上看,这三个全称命题的否定都变成了存在性命题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com