
4、________________________________________________。
[典例示范]
例1 已知函数f(x)=2ax+1(a≠0)在(0,1)上存在零点,求实数a的取值范围。
例2 用二分法求函数f(x)=8x3-16x+7在区间(-1,1)上的零点。

[巩固强化]
3、________________________________________________。
2、________________________________________________。
1、________________________________________________。
1、函数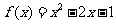 在下列哪个区间内有零点 ( )
在下列哪个区间内有零点 ( )
A  B
B  C
C  D
D 
2、观察下面的函数图象,

该函数在区间(a,b)、 (b,c)、 (a,d)内是否有零点?
观察这三个区间端点函数值f(a)、f(b)、f(c)、、f(d)的符号,你发现 f(a)·f(b)、 f(b)·f(c)、 f(a)·f(d)具有什么共同点?
[归纳总结1]
如果函数y=f(x)在区间[a,b]上的图象不间断,那么在什么条件下,函数y=f(x)在区间(a,b)内一定存在零点?
跟踪练习2:已知函数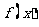 的图象是不间断的,x、
的图象是不间断的,x、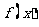 的对应关系见下表,则函数
的对应关系见下表,则函数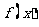 存在零点的区间有( )
存在零点的区间有( )
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
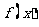 |
6 |
5 |
-3 |
10 |
-5 |
-23 |
A  B
B  C
C  D
D 
思考1:满足上述条件的函数y=f(x)在区间(a,b)上的零点的个数是否唯一?
思考2:若把条件“f(a)·f(b)<0”改为“f(a)·f(b)>0”, 函数y=f(x)在区间
(a,b)上是否不存在零点?
思考3:根据条件“f(a)·f(b)<0”确定地是函数的变号零点还是不变号零点?
[合作探究二]求函数零点近似解的方法的探索:
1、请找出下列函数的零点所在的区间:
① ___________ A
___________ A  B
B  C
C
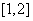 D
D
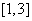
②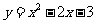 ___________ A
___________ A 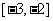 B
B
 C
C
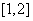 D
D

2、请给出变号零点与不变号零点的严格定义:
如果函数图象 ,则称这样的零点为变号零点。
如果函数图象 ,则称这样的零点为不变号零点。
跟踪练习1:函数f(x)的图象如图所示,则该函数变号零点的个数是 个。

[合作探究一]零点存在性的探索:
1、画出函数 的图象,并找出它们的零点。
的图象,并找出它们的零点。

观察上述图象,你发现它们在零点两侧函数值的符号有何不同?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com