
6.为了得到函数 y = 3×( ) x 的图象,可以把函数 y = ( ) x 的图象 ( )
A.向左平移 3 个单位长度 B.向右平移 3 个单位长度
C.向左平移 1 个单位长度 D. 向右平移 1 个单位长度
5. 函数 f (x) =ax3+(a-1)x2+(b-3)x+b的图象关于原点成中心对称,则 f (x) ( )
A.有极大值和极小值 B.有极大值无极小值
C.无极大值有极小值 D. 无极大值无极小值
4. 已知函数 f (x)=x2+1(x>0),那么 f -1 (10) = ( )
A.101 B.99 C.3 D. -3
3.设 f (x) = ,则 f (f (2)) = ( )
A.-2 B.2 C.5 D. 26
2.如果映射f:A→B满足集合B中的任意一个元素在A中都有原象,则称为“满射”.若集
合A中有3个元素,集合B中有2个元素,则从A到B的不同满射的个数为 ( )
A.2 B.4 C.6 D.8
1. 若集合 A = {1,2,3},B = {0,1,2,5},则U= A∪B ,则∁U (A∩B)的元素的个数为( )
A.2 B.3 C.4 D.5
48.解:⑴由题意得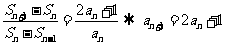 4′
4′

 (n≥2),又∵
(n≥2),又∵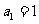 ,
,
 数列
数列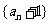 是以
是以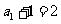 为首项,以2为公比的等比数列。 8′
为首项,以2为公比的等比数列。 8′
[则

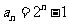 (
(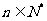 )]
)]
⑵由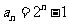 及
及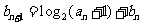 得
得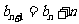

 , 则
, 则
 13′
13′


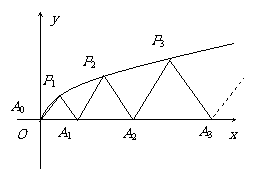
38.解:(1) 由已知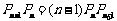 ,
,
令n = 2,P1P2 = P2P3,所以a2 = 1,····························································· 1分
令n = 3,P2P3 =
2P3P4,所以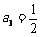 ,·························································· 2分
,·························································· 2分
同理, .
.
所以 ······· 5分
······· 5分
(2) 因为
所以
 .
.
而n = 1时,易知a1 = 1 < 3成立,所以 ······· 10分
······· 10分
(3) 假设有两个点A(p,ap),B(q,aq) ,都在函数
,都在函数
即 .所以
.所以 .
.
消去k得 ,……①
,……①
以下考查数列{bn}, 的增减情况,
的增减情况,
 ,
,
当n > 2时,n2 – 3n + 1 > 0,所以对于函数{bn}有b2 > b3 > b4 > … > bn > …
所以①式不能成立,
所以,不可能有两个点同时在函数 图像上.···························· 14分
图像上.···························· 14分
41解析: (Ⅰ) 设第n个集合中最小数an , 则第 个集合中最小数
个集合中最小数 ,
,
又第 个集合中共有
个集合中共有 个数, 且依次增加2 ,
个数, 且依次增加2 ,
∴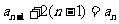 ,即
,即  , ------2分
, ------2分
∴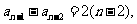

 ,
,
相加得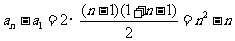 ,即得
,即得 .
.
又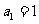 ,
∴
,
∴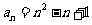 .
------4分
.
------4分
(Ⅱ)由(Ⅰ)得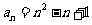 ,
,
从而得 .
- -----8分
.
- -----8分
(Ⅲ)由(Ⅱ)得 , ∴
, ∴
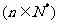 ,
,
∵
≥ , -
-----10分
, -
-----10分
又当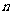 ≥2 时,
≥2 时, 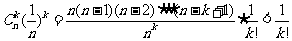
≤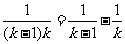 .
- -----12分
.
- -----12分
∴
≤
 .
.
∴ 2≤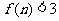 .
–
.
–
34. 解:(Ⅰ)  .…………………………………………… 2分
.…………………………………………… 2分
(Ⅱ)依题意 ,则
,则
 ,
, … 3分
… 3分
在正三角形 中,有
中,有
 .
.
 .…………………………………………………… 4分
.…………………………………………………… 4分
 ,
,
 ,
①
,
①
同理可得 . ②
. ②
①-②并变形得

 ,
,
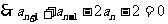 ,
…………………………………
6分
,
…………………………………
6分
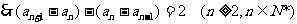 .
.
∴数列 是以
是以 为首项,公差为
为首项,公差为 的等差数列.
的等差数列.
 , …………………………………… 7分
, …………………………………… 7分

 ,
,

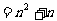 .
.
 .
………………………… 8分
.
………………………… 8分
(Ⅲ)解法1 :∵ ,
,
∴ .
.


 .
.
∴当 时,上式恒为负值,
时,上式恒为负值,
∴当 时,
时, ,
,
∴数列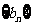 是递减数列.
是递减数列.
 的最大值为
的最大值为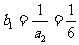 . ………………………………………………… 11分
. ………………………………………………… 11分
若对任意正整数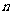 ,当
,当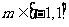 时,不等式
时,不等式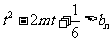 恒成立,则不等式
恒成立,则不等式 在
在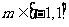 时恒成立,即不等式
时恒成立,即不等式 在
在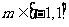 时恒成立.
时恒成立.
设 ,则
,则 且
且 ,
,
∴
解之,得 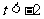 或
或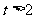 ,
,
即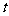 的取值范围是
的取值范围是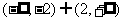 .…………………………………………… 14分
.…………………………………………… 14分
30.解:(Ⅰ)因为 所以
所以

一般地,当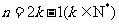 时,
时,
= ,即
,即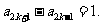
所以数列 是首项为1、公差为1的等差数列,因此
是首项为1、公差为1的等差数列,因此
当 时,
时,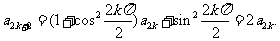
所以数列 是首项为2、公比为2的等比数列,因此
是首项为2、公比为2的等比数列,因此
故数列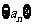 的通项公式为
的通项公式为
(Ⅱ)由(Ⅰ)知,
 ①
①
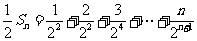 ②
②
①-②得,

所以
要证明当 时,
时, 成立,只需证明当
成立,只需证明当 时,
时, 成立.
成立.
证法一
(1)当n = 6时, 成立.
成立.
(2)假设当 时不等式成立,即
时不等式成立,即
则当n=k+1时,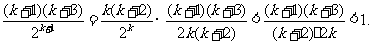
由(1)、(2)所述,当n≥6时, .即当n≥6时,
.即当n≥6时,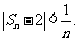
证法二
令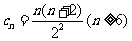 ,则
,则
所以当 时,
时, .因此当
.因此当 时,
时,
于是当 时,
时, 综上所述,当
综上所述,当 时,
时,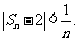
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com