
24.- Why was Professor Liu thundering in the classroom yesterday?
- A student’s interrupting his speech the burst of his anger.
A. set up B. set out C. set about D. set off
23.- Sunny day, isn’t it?
- Let’s hope the sunny weather for Saturday’s tennis match.
A. carries on B. moves on C. keeps up D. goes up
22.The rich only themselves in making money and had no eye for the needs and welfare of
their workers
A. devoted B. concerned C. enjoyed D. occupied
第一节:单项选择(共10小题;每小题1分,满分10分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21.Many middle school teachers are too heavily with teaching to engage in research work.
A. burdened B. related C. associated D. provided
21.解:(1) 由
相减得: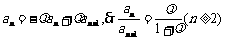 ,
,
 数列
数列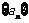 是等比数列。
是等比数列。
(2) ,
,
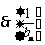 是首项为
是首项为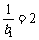 ,公差为1的等差数列;
,公差为1的等差数列; ,
,
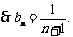
(3)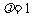 时,
时,
 ,
①
,
①
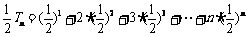 ②
②
①-②得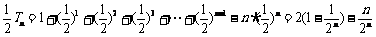 ,
,
 ,
,
又因为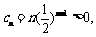
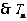 单调递增,
单调递增, 时
时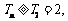
故当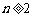 时,
时,
21.(本小题满分14分)设数列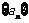 的前
的前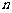 项和为
项和为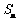 ,且
,且 ,其中
,其中 为常数,且
为常数,且 、0.
、0.
(1)证明:数列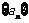 是等比数列;
是等比数列;
(2)设数列 的公比
的公比 ,数列
,数列 满足
满足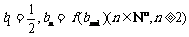 ,求数列
,求数列
 的通项公式;
的通项公式;
(3)设 ,数列
,数列 的前
的前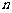 项和为
项和为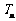 ,求证:当
,求证:当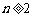 时,
时,
20.解析:(1)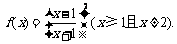
∵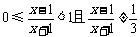 ,∴函数
,∴函数 的值域为
的值域为
由 ,得
,得 ,因此,函数
,因此,函数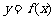 的反函数
的反函数

(2)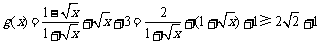 ,当且仅当
,当且仅当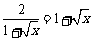 ,
,
即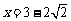 时,
时, 有最小值
有最小值
(3)由 ,得
,得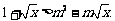
设 ,则
,则
根据题意,对区间 中的一切t值,
中的一切t值,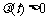 恒成立.
恒成立.
则 得
得 ∴
∴
∴ 即实数m的取值范围是
即实数m的取值范围是
20.(本小题满分13分)已知函数 (其中x≥1且x≠2).
(其中x≥1且x≠2).
(1)求函数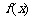 的反函数
的反函数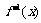 ;
;
(2)设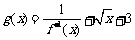 ,求函数
,求函数 最小值及相应的x值;
最小值及相应的x值;
(3)若不等式 对于区间
对于区间 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.
19.解析:(1)由题知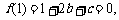
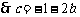
记 ,
,
则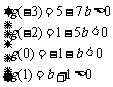
 ,
即
,
即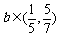 .
.
(2)令 ,
,
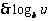 在区间
在区间 上是减函数.
上是减函数.
而 ,函数
,函数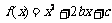 的对称轴为
的对称轴为 ,
,
 在区间
在区间 上单调递增.
上单调递增.
从而函数 在区间
在区间 上为减函数.
上为减函数.
且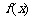 在区间
在区间 上恒有
上恒有 ,只需要
,只需要 ,
,

19.(本小题满分12分)已知二次函数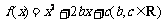 满足
满足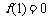 ,且关于
,且关于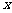 的方程
的方程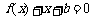 的两个实数根分别在区间
的两个实数根分别在区间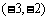 、
、 内.
内.
(1)求实数 的取值范围;
的取值范围;
(2)若函数 在区间
在区间 上具有单调性,求实数
上具有单调性,求实数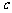 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com