6、仅在2008元旦前后三天，欧美亚报刊上就出现了一批醒目的大字标题：英国《卫报》──《中国崛起比9•11事件更具影响》，法新社新闻网──《中国崛起迹象随处可见》，美国《新闻周刊》──《中国一个强悍又脆弱大国的崛起》，新加坡《联合早报》──《面对中国崛起西方进退失据》……。中国用“和平崛起”来描述自己的未来形象，这体现了我们传统文化中的

① 民为贵，君为轻　　　 　　　　　 ② 人性本善　

③ 已欲立而立人，已欲达而达人　 　④ 已所不欲，勿施于人

A．①③　　　　　　　 　　 B．②④　　　　　　　 　　 C．②③　　　　 　　　 D．③④

5、下列选项中正确反映了1870-1956年中国民族资本主义发展趋势的是

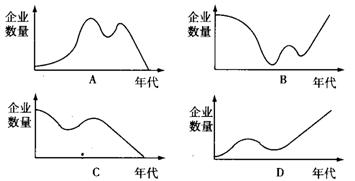
4、1784年刚刚获得独立的美国为了打破英国组织的经济封锁，派遣商船中国皇后号来华开展贸易，该船在中国停靠的港口应该是：

　　 A．宁波　　　　　　 B．上海　　　 C．厦门　　　　 D．广州

3、1932年，英国外交大臣张伯伦曾说：“由于某种难以确切指出的东西，世界近两年正在倒退。各国相互之间不是更加接近，不是在增进友谊，不是在向稳定的和平迈进，而是采取了一种危及世界和平的猜疑、恐惧和危险的态度。”张伯伦不能确定的“某种东西”应该是:　

　 　　A．法西斯及其侵略扩张　　　　　　　 B．苏联及其社会主义的影响

　 　　C．罗斯福新政及其影响　　　　　　　 D．大萧条及其影响

2、2007年12月，宋代沉船“南海一号”的打捞吸引了全球的目光。考古工作者已经从南海一号上整理出大量珍贵的文物。以下文物不可能从该船发现的是

1.下面图一到图二两则史料的变化可以直接用来论证　　　　　　　　　　

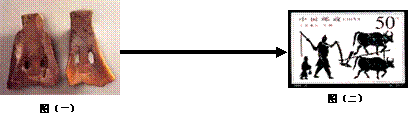
A．我国古代农业经营方式的变化　 　　　B．我国古代手工业技术的进步

C．我国古代经济结构的变化　　　　　　 D．我国古代农业耕作方式的变化

答案：1.⑴真；⑵真；⑶假.

2.⑴p或q：4∈{2，3}或2∈{2，3}；p且q：4∈{2，3}且2∈{2，3}；非p：4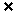{2，3}.

∵p假q真，∴“p或q”为真，“p且q”为假，“非p”为真.

⑵p或q：2是偶数或不是质数；p且q：2是偶数且不是质数；非p：2不是偶数.

∵p真q假，∴“p或q”为真，“p且q”为假，“非p”为假.

5．学习逻辑的意义

一方面是因为数学基础需要用逻辑来阐明，另一方面是因为计算机离不开数学逻辑，课本中介绍的洗衣机上的“或门电路”和电子保险门上的“与门电路”就是两个在这方面应用的实例.可以说计算机的“智能”装置是以数学逻辑为基础进行设计的.

同学们可以结合日常生活中电器的自动控制功能，再找出一些这样的例子.

电路：

或门电路(或)　　　　 与门电路(且)

4．逻辑符号

“或”的符号是“∨”，“且”的符号是“∧”，“非”的符号是“┐”.

例如，“p或q”可记作“p∨q”； “p且q”可记作“p∧q”；“非p”可记作“┐p”.

注意：数学中的“或”与日常生活用语中的“或”的区别

“或”这个逻辑联结词的用法，一般有两种解释：

一是“不可兼有”，即“a或b”是指a，b中的某一个，但不是两者.日常生活中有时采用这一解释.例如“你去或我去”，人们在理解上不会认为有你我都去这种可能.

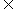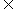二是“可兼有”，即“a或b”是指a，b中的任何一个或两者.例如“xA或xB”，是指x可能属于A但不属于B(这里的“但”等价于“且”)，x也可能不属于A但属于B，x还可能既属于A又属于B(即x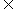A∩B)；又如在“p真或q真”中，可能只有p真，也可能只有q真，还可能p,q都为真.数学书中一般采用这种解释，运用数学语言和解数学题时，都要遵守这一点.还要注意“可兼有”并不意味“一定兼有”.

另外，“苹果是长在树上或长在地里”这一命题，按真值表判断，它是真命题，但在日常生活中，我们认为这句话是不妥的.

3．“p或q”形式的复合命题：

例3．如果p表示“5是12的约数” q表示“5是15的约数”，r表示“5是8的约数”，写出，p或r，q或s，p或q的复合命题，并判断其真假，归纳其规律.

p或q即“5是12的约数或是15的约数”为真(p为假、q为真)；

p或r即“5是12的约数或是8的约数”为假(p、r为假)

小结：“p或q”形式的复合命题真假判断

当p，q中至少有一个为真时，“p或q”为真；当p，q都为假时，“p或q”为假. 即“p或q”形式的复合命题，当p与q同为假时为假，其他情况时为真. 可用下表表示.

像上面三个表用来表示命题的真假的表叫做真值表.

在真值表中，是根据简单命题的真假，判断由这些简单命题构成的复合命题的真假，而不涉及简单命题的具体内容.

例4(课本第28页例2)分别指出由下列各组命题构成的“ p或q”，“p且q”，“非p”形式的复合命题的真假：

① p：2+2=5，q：3>2；

② p：9是质数，q：8是12的约数；

③ p：1∈{1，2}，q：{1}{1，2}；

④ p：φ{0}，q：φ={0}.

解：①p或q：2+2=5或3>2 ；p且q：2+2=5且3>2 ；非p：2+2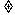5.

∵p假q真，∴“p或q”为真，“p且q”为假，“非p”为真.

②p或q：9是质数或8是12的约数；p且q：9是质数且8是12的约数；非p：9不是质数.

∵p假q假，∴“p或q”为假，“p且q”为假，“非p”为真.

③p或q：1∈{1，2}或{1}{1，2}；p且q：1∈{1，2}且{1}{1，2}；非p：1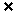{1，2}.

∵p真q真，∴“p或q”为真，“p且q”为真，“非p”为假.

④p或q：φ{0}或φ={0}；p且q：φ{0}且φ={0} ；非p：φ{0}.

∵p真q假，∴“p或q”为真，“p且q”为假，“非p”为假.