
(一)选择题:
1、(07陕西)抛物线 的准线方程是( )
的准线方程是( )
A、 B、
B、 C、
C、 D、
D、
2、(07海南)已知抛物线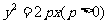 的焦点为
的焦点为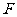 ,点
,点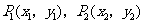 ,
, 在抛物线上,且
在抛物线上,且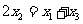 ,则有( )
,则有( )
A、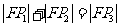 B、
B、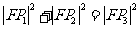
C、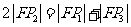 D、
D、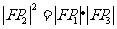
3、(07全国Ⅰ11)抛物线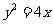 的焦点为
的焦点为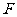 ,准线为
,准线为 ,经过
,经过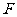 且斜率为
且斜率为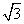 的直线与抛物线在
的直线与抛物线在 轴上方的部分相交于点
轴上方的部分相交于点 ,
, ,垂足为
,垂足为 ,则
,则 的面积是( )
的面积是( )
A、 B、
B、 C、
C、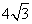 D、
D、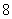
4、(06四川)直线 与抛物线
与抛物线 交于
交于 两点,过
两点,过 两点向抛物线的准线作垂线,垂足分别为
两点向抛物线的准线作垂线,垂足分别为 ,则梯形
,则梯形 的面积为( )
的面积为( )
A、48. B、56 C、64 D、72
5、(06江西)设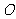 为坐标原点,
为坐标原点,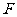 为抛物线
为抛物线 的焦点,
的焦点, 是抛物线上一点,若
是抛物线上一点,若 ,则点
,则点 的坐标是( )
的坐标是( )
A、(2,±2 ) B、
(1,±2) C、(1,2) D、(2,2
) B、
(1,±2) C、(1,2) D、(2,2 )
)
6、(05上海)过抛物线 的焦点作一条直线与抛物线相交于
的焦点作一条直线与抛物线相交于 两点,它们的横坐标之和等于5,则这样的直线( )
两点,它们的横坐标之和等于5,则这样的直线( )
A、有且仅有一条 B、有且仅有两条 C、有无穷多条 D、不存在
7、(05江苏)抛物线 上的一点
上的一点 到焦点的距离为1,则
到焦点的距离为1,则 点的纵坐标是( )
点的纵坐标是( )
A、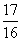 B、
B、 C、
C、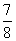 D、0
D、0
例1、(08上海春)在平面直角坐标系 中,
中, 分别为直线
分别为直线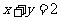 与
与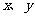 轴的交点,
轴的交点,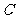 为
为 的中点. 若抛物线
的中点. 若抛物线 过点
过点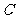 ,求焦点
,求焦点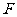 到直线
到直线 的距离。
的距离。
例2、(07山东)设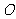 是坐标原点,
是坐标原点,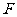 是抛物线
是抛物线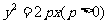 的焦点,
的焦点, 是抛物线上的一点,
是抛物线上的一点,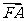 与
与 轴正向的夹角为
轴正向的夹角为 ,则
,则 为
;
为
;
例3、(07全国Ⅱ12)设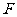 为抛物线
为抛物线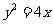 的焦点,
的焦点,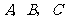 为该抛物线上三点,若
为该抛物线上三点,若 ,则
,则 ( )
( )
A、9 B、6 C、4 D、3
例4、(07湖北19)在平面直角坐标系 中,过定点
中,过定点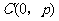 作直线与抛物线
作直线与抛物线 (
( )相交于
)相交于 两点。
两点。
(I)若点 是点
是点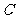 关于坐标原点
关于坐标原点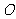 的对称点,求
的对称点,求 面积的最小值;
面积的最小值;
(II)是否存在垂直于 轴的直线
轴的直线 ,使得
,使得 被以
被以 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
例5、(05全国Ⅲ21)设 ,
, 两点在抛物线
两点在抛物线 上,
上, 是
是 的垂直平分线。(Ⅰ)当且仅当
的垂直平分线。(Ⅰ)当且仅当 取何值时,直线
取何值时,直线 经过抛物线的焦点
经过抛物线的焦点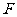 ?证明你的结论;(Ⅱ)当直线
?证明你的结论;(Ⅱ)当直线 的斜率为2时,求
的斜率为2时,求 在
在 轴上截距的取值范围。
轴上截距的取值范围。
解:(Ⅰ) 两点到抛物线的准线的距离相等,
两点到抛物线的准线的距离相等,
∵抛物线的准线是 轴的平行线,
轴的平行线, ,依题意
,依题意 不同时为0
不同时为0
∴上述条件等价于
∵
∴上述条件等价于
即当且仅当 时,
时, 经过抛物线的焦点
经过抛物线的焦点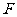 。
。
(Ⅱ)设 在
在 轴上的截距为
轴上的截距为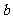 ,依题意得
,依题意得 的方程为
的方程为 ;过点
;过点 的直线方程可写为
的直线方程可写为 ,所以
,所以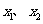 满足方程
满足方程
得
 为抛物线上不同的两点等价于上述方程的判别式
为抛物线上不同的两点等价于上述方程的判别式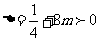 ,即
,即
设 的中点
的中点 的坐标为
的坐标为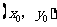 ,则
,则
 ,
,
由 ,得
,得 ,于是
,于是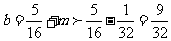
即得 在
在 轴上截距的取值范围为
轴上截距的取值范围为 。
。
例6、(05天津21)抛物线C的方程为 ,过抛物线
,过抛物线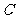 上一点
上一点  (
(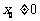 )作斜率为
)作斜率为 的两条直线分别交抛物线
的两条直线分别交抛物线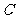 于
于 ,
, 两点(
两点( 三点互不相同),且满足
三点互不相同),且满足 (
( ≠0且
≠0且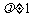 )。
)。
(Ⅰ)求抛物线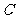 的焦点坐标和准线方程;
的焦点坐标和准线方程;
(Ⅱ)设直线 上一点
上一点 ,满足
,满足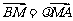 ,证明线段
,证明线段 的中点在
的中点在 轴上;
轴上;
(Ⅲ)当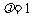 时,若点
时,若点 的坐标为(1,
的坐标为(1, 1),求
1),求 为钝角时点
为钝角时点 的纵坐标
的纵坐标 的取值范围。
的取值范围。
解:(I)由抛物线 的方程
的方程 得,焦点坐标为(
得,焦点坐标为( ),准线方程为
),准线方程为
(II)证明:设直线PA的方程为 ,直线PB的方程为
,直线PB的方程为
点 和点
和点 的坐标是方程组
的坐标是方程组 的解
的解
将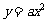 代入
代入 得:
得: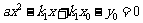
由韦达定理: ①
①
同理: ,又因为
,又因为 ,所以
,所以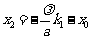 ②
②
设点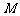 的坐标为
的坐标为 ,由
,由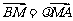 ,得
,得 ③
③
将
② 代入 ③ 得:
即: 。所以,线段
。所以,线段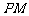 的中点在
的中点在 轴上
轴上
(III)解:因为点P(1, 1)在抛物线
1)在抛物线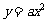 上,所以
上,所以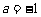 ,抛物线的方程为
,抛物线的方程为 。
。
由
① 得: ,代入
,代入 得
得
将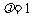 代入 ② ,得
代入 ② ,得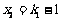 ,代入
,代入 得
得
因此,直线PA、PB分别与抛物线C的交点A、B的坐标为
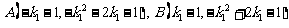
于是: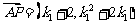 ,
,

因为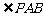 为钝角且P、A、B三点互不相同,故必有
为钝角且P、A、B三点互不相同,故必有 ,即
,即
解得 的范围为:
的范围为: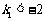 或
或
又点A的纵坐标 满足
满足 ,故
,故
当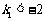 时,
时,
当 时,
时,
所以,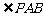 为钝角时,点A的纵坐标
为钝角时,点A的纵坐标 的取值范围是
的取值范围是 。
。
(三)解答题:
7、(07江西21)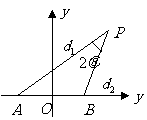 设动点
设动点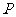 到点
到点 和
和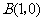 的距离分别为
的距离分别为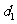 和
和 ,
, ,且存在常数
,且存在常数 ,使得
,使得 .
.
(1)证明:动点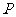 的轨迹
的轨迹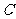 为双曲线,并求出
为双曲线,并求出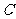 的方程;
的方程;
(2)过点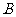 作直线双曲线
作直线双曲线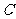 的右支于
的右支于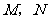 两点,试确定
两点,试确定 的范围,使
的范围,使 ,其中点
,其中点 为坐标原点.
为坐标原点.
解法一:(1)在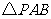 中,
中, ,即
,即 ,
,
 ,即
,即 (常数),
(常数),
点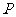 的轨迹
的轨迹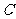 是以
是以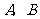 为焦点,实轴长
为焦点,实轴长 的双曲线.
的双曲线.
方程为: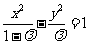 .
.
(2)设 ,
,
①当 垂直于
垂直于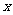 轴时,
轴时, 的方程为
的方程为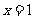 ,
, ,
, 在双曲线上.
在双曲线上.
即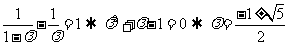 ,因为
,因为 ,所以
,所以 .
.
②当 不垂直于
不垂直于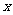 轴时,设
轴时,设 的方程为
的方程为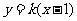 .
.
由 得:
得: ,
,
由题意知: ,
,
所以 ,
, .
.
于是: .
.
因为 ,且
,且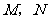 在双曲线右支上,所以
在双曲线右支上,所以
 .
.
由①②知, .
.
解法二:(1)同解法一
(2)设 ,
, ,
, 的中点为
的中点为 .
.
①当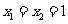 时,
时,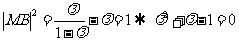 ,
,
因为 ,所以
,所以 ;
;
②当 时,
时, .
.
又 .所以
.所以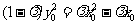 ;
;
由 得
得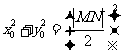 ,由第二定义得
,由第二定义得
 .
.
所以 .
.
于是由 得
得
因为 ,所以
,所以 ,又
,又 ,
,
解得: .由①②知
.由①②知 .
.
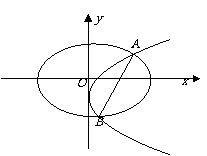
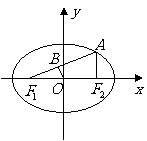
8、(07上海21)我们把由半椭圆
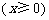 与半椭圆
与半椭圆
 合成的曲线称作“果圆”,其中
合成的曲线称作“果圆”,其中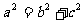 ,
, ,
, .如图,点
.如图,点 ,
, ,
,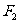 是相应椭圆的焦点,
是相应椭圆的焦点, ,
, 和
和 ,
, 分别是“果圆”与
分别是“果圆”与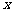 ,
, 轴的交点.
轴的交点.
 (1)若
(1)若 是边长为1的等边三角形,求“果圆”的方程;
是边长为1的等边三角形,求“果圆”的方程;
(2)当

 时,求
时,求 的取值范围;
的取值范围;
(3)连接“果圆”上任意两点的线段称为“果圆”
的弦.试研究:是否存在实数 ,使斜率为
,使斜率为 的“果圆”
的“果圆”
平行弦的中点轨迹总是落在某个椭圆上?若存在,求出所有可能的 值;若不存在,说明理由.
值;若不存在,说明理由.
解:(1)
 ,
,
 ,
,
于是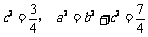 ,所求“果圆”方程为
,所求“果圆”方程为
 ,
,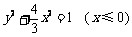 .
.
(2)由题意,得 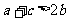 ,即
,即 .
.
 ,
, ,得
,得 .
.
又 .
.  .
.
(3)设“果圆”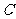 的方程为
的方程为 ,
, .
.
记平行弦的斜率为 .
.
当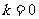 时,直线
时,直线 与半椭圆
与半椭圆 的交点是
的交点是
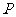
 ,与半椭圆
,与半椭圆 的交点是
的交点是
 .
.

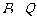 的中点
的中点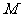
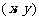 满足
满足 
得
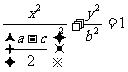 .
.

 ,
,
 .
.
综上所述,当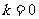 时,“果圆”平行弦的中点轨迹总是落在某个椭圆上.
时,“果圆”平行弦的中点轨迹总是落在某个椭圆上.
当 时,以
时,以 为斜率过
为斜率过 的直线
的直线 与半椭圆
与半椭圆 的交点是
的交点是 .
.
由此,在直线 右侧,以
右侧,以 为斜率的平行弦的中点轨迹在直线
为斜率的平行弦的中点轨迹在直线 上,即不在某一椭圆上.
上,即不在某一椭圆上.
当 时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上.
时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上.
9、(06湖南21)已知椭圆 , 抛物线
, 抛物线 , 且
, 且 的公共弦
的公共弦 过椭圆
过椭圆 的右焦点。(Ⅰ) 当
的右焦点。(Ⅰ) 当 轴时, 求
轴时, 求 的值, 并判断抛物线
的值, 并判断抛物线 的焦点是否在直线
的焦点是否在直线 上;(Ⅱ) 是否存在
上;(Ⅱ) 是否存在 的值, 使抛物线
的值, 使抛物线 的焦点恰在直线
的焦点恰在直线 上? 若存在, 求出符合条件的
上? 若存在, 求出符合条件的 的值; 若不存在, 请说明理由。
的值; 若不存在, 请说明理由。
解:(Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为:
x =1,从而点A的坐标为(1, )或(1,-
)或(1,- ). 因为点A在抛物线上.
). 因为点A在抛物线上.
所以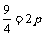 ,即
,即 .此时C2的焦点坐标为(
.此时C2的焦点坐标为(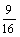 ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.
(II)解法一: 假设存在 、
、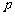 的值使
的值使 的焦点恰在直线AB上,由(I)知直线AB
的焦点恰在直线AB上,由(I)知直线AB
的斜率存在,故可设直线AB的方程为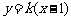 .
.
 由
由 消去
消去 得
得 ………………①
………………①
设A、B的坐标分别为(x1,y1), (x2,y2),
则x1,x2是方程①的两根,x1+x2=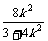 .
.
由
消去y得 . ………………②
. ………………②
因为C2的焦点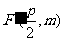 在直线
在直线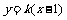 上,
上,
所以 ,即
,即 .代入②有
.代入②有 .
.
即 .
…………………③
.
…………………③
由于x1,x2也是方程③的两根,所以x1+x2= .
.
从而 =
= . 解得
. 解得 ……………………④
……………………④
又AB过C1、、\、、C2的焦点,所以
 ,
,
则 …………………………………⑤
…………………………………⑤
由④、⑤式得 ,即
,即 .
.
解得 于是
于是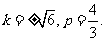
因为C2的焦点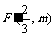 在直线
在直线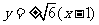 上,所以
上,所以 .
.

 或
或 .
.
由上知,满足条件的 、
、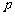 存在,且
存在,且 或
或 ,
, .
.
解法二: 设A、B的坐标分别为 ,
, .
.
因为AB既过C1的右焦点 ,又过C2的焦点
,又过C2的焦点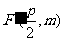 ,
,
所以 .
.
即 .
……①
.
……①
由(Ⅰ)知 ,于是直线AB的斜率
,于是直线AB的斜率 , ……②
, ……②
且直线AB的方程是 ,
,
所以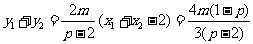 . ……③
. ……③
又因为 ,所以
,所以 . ……④
. ……④
将①、②、③代入④得 . ……………⑤
. ……………⑤
因为 ,所以
,所以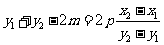 . …………⑥
. …………⑥
将②、③代入⑥得 ……………⑦
……………⑦
由⑤、⑦得
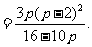 即
即
解得 .将
.将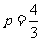 代入⑤得
代入⑤得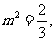

 或
或 .
.
由上知,满足条件的 、
、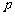 存在,且
存在,且 或
或 ,
,
(二)填空题:
5、(05江西16)以下同个关于圆锥曲线的命题中
①设 为两个定点,
为两个定点, 为非零常数,
为非零常数, ,则动点
,则动点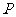 的轨迹为双曲线;
的轨迹为双曲线;
②设定圆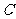 上一定点
上一定点 作圆的动点弦
作圆的动点弦 ,
, 为坐标原点,若
为坐标原点,若 则动点
则动点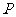 的轨迹为椭圆;
的轨迹为椭圆;
③方程 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线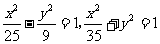 (椭圆)有相同的焦点。其中真命题的序号为
(椭圆)有相同的焦点。其中真命题的序号为
(写出所有真命题的序号)
6、(04山东16)设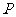 为曲线
为曲线 上的一个动点,则点
上的一个动点,则点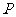 到点(0,1)的距离与点
到点(0,1)的距离与点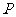 到
到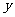 轴的距离之和的最小值为_________。
轴的距离之和的最小值为_________。
(一)选择题:
1、(06安徽)若抛物线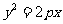 的焦点与椭圆
的焦点与椭圆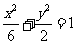 的右焦点重合,则
的右焦点重合,则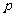 的值为
的值为
A、 B、
B、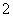 C、
C、 D、
D、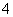
2、(06江西)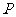 是双曲线
是双曲线 的右支上一点,
的右支上一点, 分别是圆
分别是圆 和
和 上的点,则
上的点,则 的最大值为( )
的最大值为( )
A、6 B、7 C、8 D、9
3、(05湖北)双曲线 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线 的焦点重合,则
的焦点重合,则 的值为( )
的值为( )
A、 B、
B、 C、
C、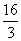 D、
D、
4、(05天津)设双曲线以椭圆 长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为( )
长轴的两个端点为焦点,其准线过椭圆的焦点,则双曲线的渐近线的斜率为( )
A、 B、
B、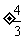 C、
C、 D、
D、
例1、(07天津22)设椭圆 的左、右焦点分别为
的左、右焦点分别为 是椭圆上的一点,
是椭圆上的一点, ,原点
,原点 到直线
到直线 的距离为
的距离为 .
.
(Ⅰ)证明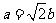 ;
;
(Ⅱ)设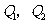 为椭圆上的两个动点,
为椭圆上的两个动点,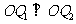 ,过原点
,过原点 作直线
作直线 的垂线
的垂线 ,垂足为
,垂足为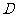 ,求点
,求点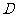 的轨迹方程.
的轨迹方程.
(Ⅰ)证法一:由题设 及
及 ,
, ,不妨设点
,不妨设点 ,其中
,其中 .由于点
.由于点 在椭圆上,有
在椭圆上,有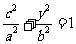 ,即
,即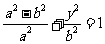 .
.
解得 ,从而得到
,从而得到 .
.
直线 的方程为
的方程为 ,整理得
,整理得 .
.
由题设,原点 到直线
到直线 的距离为
的距离为 ,即
,即 ,
,
将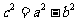 代入上式并化简得
代入上式并化简得 ,即
,即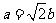 .
.
证法二:同证法一,得到点 的坐标为
的坐标为 .
.
过点 作
作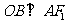 ,垂足为
,垂足为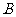 ,易知
,易知

 ,故
,故 .
.
 由椭圆定义得
由椭圆定义得 ,又
,又 ,
,
所以 ,
,
解得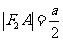 ,而
,而 ,得
,得 ,即
,即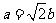 .
.
(Ⅱ)解法一:设点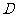 的坐标为
的坐标为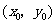 .
.
当 时,由
时,由 知,直线
知,直线 的斜率为
的斜率为 ,所以直线
,所以直线 的方程为
的方程为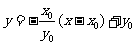 ,或
,或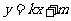 ,其中
,其中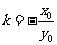 ,
, .
.
点 的坐标满足方程组
的坐标满足方程组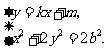
将①式代入②式,得 ,
,
整理得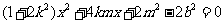 ,
,
于是 ,
,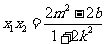 .
.
由①式得
 .
.
由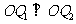 知
知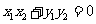 .将③式和④式代入得
.将③式和④式代入得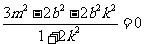 ,
,
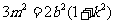 .
.
将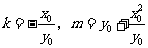 代入上式,整理得
代入上式,整理得 .
.
当 时,直线
时,直线 的方程为
的方程为 ,
, 的坐标满足方程组
的坐标满足方程组
所以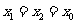 ,
, .
.
由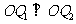 知
知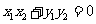 ,即
,即 ,
,
解得 .
.
这时,点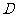 的坐标仍满足
的坐标仍满足 .
.
综上,点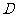 的轨迹方程为
的轨迹方程为 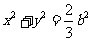 .
.
解法二:设点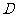 的坐标为
的坐标为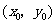 ,直线
,直线 的方程为
的方程为 ,由
,由 ,垂足为
,垂足为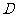 ,可知直线
,可知直线 的方程为
的方程为 .
.
记 (显然
(显然 ),点
),点 的坐标满足方程组
的坐标满足方程组
由①式得 . ③
. ③
由②式得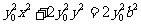 . ④
. ④
将③式代入④式得 .
.
整理得 ,
,
于是 . ⑤
. ⑤
由①式得 . ⑥
. ⑥
由②式得 . ⑦
. ⑦
将⑥式代入⑦式得 ,
,
整理得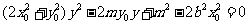 ,
,
于是 . ⑧
. ⑧
由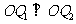 知
知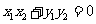 .将⑤式和⑧式代入得
.将⑤式和⑧式代入得 ,
,
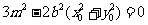 .
.
将 代入上式,得
代入上式,得 .
.
所以,点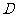 的轨迹方程为
的轨迹方程为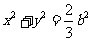 .
.
例2、(06重庆22)已知一列椭圆 :
: ,
,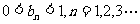 ,若椭圆
,若椭圆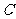 上有一点
上有一点 使
使 到右准线
到右准线 的距离
的距离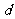 是
是 |与
|与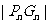 的等差中项,其中
的等差中项,其中 分别是
分别是 的左、右焦点。
的左、右焦点。
 (Ⅰ)试证:
(Ⅰ)试证:
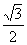
 ;
;
(Ⅱ)取
 ,并用
,并用 表示
表示 的面积,试证:
的面积,试证: 且
且
 。
。
图(22)
证:(1)由题设及椭圆的几何性质有

设


因此,由题意 应满足
应满足

即
即 ,
,
从而对任意
(Ⅱ)设点

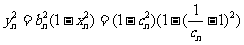
得两极 ,从而易知f(c)在(
,从而易知f(c)在(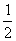 ,
, )内是增函
)内是增函 数,而在(
数,而在( ,1)内是减函数.
,1)内是减函数.
现在由题设取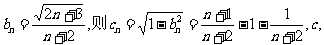 是增数列.又易知
是增数列.又易知
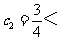

故由前已证,知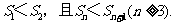
 例3、(05山东22))已知动圆过定点
例3、(05山东22))已知动圆过定点 ,且与直线
,且与直线 相切,其中
相切,其中 。(Ⅰ)求动圆圆心
。(Ⅰ)求动圆圆心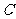 的轨迹的方程;(Ⅱ)设
的轨迹的方程;(Ⅱ)设 是轨迹
是轨迹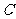 上异于原点
上异于原点 的两个不同点,直线
的两个不同点,直线 和
和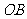 的倾斜角分别为
的倾斜角分别为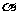 和
和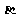 ,当
,当 变化且
变化且 为定值
为定值 时,证明直线
时,证明直线 恒过定点,并求出该定点的坐标。
恒过定点,并求出该定点的坐标。
解:(I)如图,设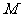 为动圆圆心,记
为动圆圆心,记 为
为 ,过点
,过点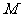 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,由题意知:
,由题意知: 即动点
即动点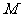 到定点
到定点 与定直线
与定直线 的距离相等
的距离相等
由抛物线的定义知,点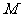 的轨迹为抛物线,其中
的轨迹为抛物线,其中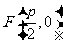 为焦点,
为焦点, 为准线
为准线
∴轨迹方程为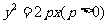 ;
;
(II)如图,设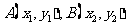 ,由题意得
,由题意得 (否则
(否则 )且
)且
∴直线 的斜率存在,设其方程为
的斜率存在,设其方程为
显然
将 与
与 联立消去
联立消去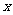 ,得
,得
由韦达定理知 ①
①
(1)当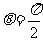 时,即
时,即 时,
时,
∴ ,
,
∴
由①知:
∴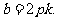
因此直线 的方程可表示为
的方程可表示为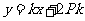 ,即
,即
∴直线 恒过定点
恒过定点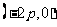
(2)当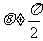 时,由
时,由 ,得
,得 =
= =
=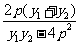
将①式代入上式整理化简可得: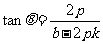 ,则
,则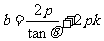 ,
,
此时,直线 的方程可表示为
的方程可表示为
 即
即
∴直线 恒过定点
恒过定点
综上,由(1)(2)知,当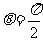 时,直线
时,直线 恒过定点
恒过定点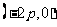 ,当
,当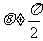 时直线
时直线 恒过定点
恒过定点 .
.
例4、(05北京18)如图,直线 :
: 与直线
与直线 :
: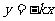 之间的阴影区域(不含边界)记为W,其左半部分记为
之间的阴影区域(不含边界)记为W,其左半部分记为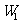 ,右半部分记为
,右半部分记为 。(Ⅰ)分别用不等式组表示
。(Ⅰ)分别用不等式组表示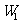 和
和 ;(Ⅱ)若区域
;(Ⅱ)若区域 中的动点
中的动点 到
到 ,
, 的距离之积等于
的距离之积等于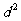 ,求点
,求点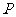 的轨迹
的轨迹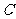 的方程;(Ⅲ)设不过原点
的方程;(Ⅲ)设不过原点 的直线
的直线 与(Ⅱ)中的曲线
与(Ⅱ)中的曲线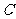 相交于
相交于 两点,且与
两点,且与 ,
, 分别交于
分别交于 两点. 求证
两点. 求证 的重心与
的重心与 的重心重合。
的重心重合。

[答案]
[详解]
解:(I)

(II)直线 直线
直线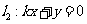 ,由题意得
,由题意得

即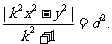
由 知
知
所以 即
即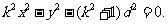
所以动点P的轨迹方程为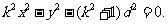
(III)当直线 与
与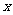 轴垂直时,可设直线
轴垂直时,可设直线 的方程为
的方程为 由于直线
由于直线 、曲线C关于
、曲线C关于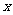 轴对称,
轴对称,
且 与
与 关于
关于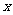 轴对称,于是
轴对称,于是 的中点坐标都为
的中点坐标都为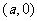 ,所以
,所以
的重心坐标都为 ,即它们的重心重合.
,即它们的重心重合.
当直线 与
与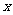 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为
由 ,得
,得
由直线  与曲线C有两个不同交点,可知
与曲线C有两个不同交点,可知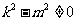 ,且
,且

设 的坐标分别为
的坐标分别为
则
设 的坐标分别为
的坐标分别为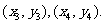
由
从而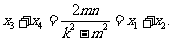
所以
所以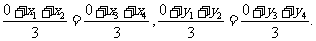
于是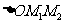 的重心与
的重心与 的重心也重合.
的重心也重合.
[名师指津]
本题为解析几何的综合题型,在高考试题中解析经常会与函数、数列、不等式、向量等综合考查各种数学思想及方法。
(三)解答题:
9、(07湖南20)已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, ,过点
,过点 的动直线与双曲线相交于
的动直线与双曲线相交于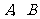 两点。
两点。
(I)若动点 满足
满足 (其中
(其中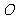 为坐标原点),求点
为坐标原点),求点 的轨迹方程;
的轨迹方程;
(II)在 轴上是否存在定点
轴上是否存在定点 ,使
,使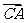 ·
·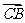 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
解:由条件知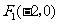 ,
, ,设
,设 ,
,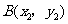 .
.
解法一:(I)设 ,则
,则 则
则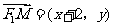 ,
, ,
,
 ,由
,由 得
得
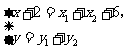 即
即
于是 的中点坐标为
的中点坐标为 .
.
当 不与
不与 轴垂直时,
轴垂直时, ,即
,即 .
.
又因为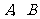 两点在双曲线上,所以
两点在双曲线上,所以 ,
, ,两式相减得
,两式相减得
 ,即
,即 .
.
将 代入上式,化简得
代入上式,化简得 .
.
当 与
与 轴垂直时,
轴垂直时, ,求得
,求得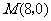 ,也满足上述方程.
,也满足上述方程.
所以点 的轨迹方程是
的轨迹方程是 .
.
(II)假设在 轴上存在定点
轴上存在定点 ,使
,使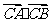 为常数.
为常数.
当 不与
不与 轴垂直时,设直线
轴垂直时,设直线 的方程是
的方程是 .
.
代入 有
有 .
.
则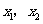 是上述方程的两个实根,所以
是上述方程的两个实根,所以 ,
,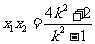 ,
,
于是

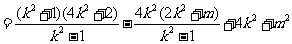
 .
.
因为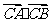 是与
是与 无关的常数,所以
无关的常数,所以 ,即
,即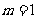 ,此时
,此时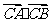 =
=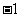 .
.
当 与
与 轴垂直时,点
轴垂直时,点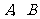 的坐标可分别设为
的坐标可分别设为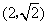 ,
, ,
,
此时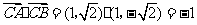 .
.
故在 轴上存在定点
轴上存在定点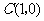 ,使
,使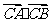 为常数.
为常数.
解法二:(I)同解法一的(I)有
当 不与
不与 轴垂直时,设直线
轴垂直时,设直线 的方程是
的方程是 .
.
代入 有
有 .
.
则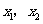 是上述方程的两个实根,所以
是上述方程的两个实根,所以 .
.
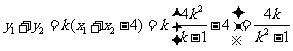 .
.
由①②③得 .…………………………………………………④
.…………………………………………………④
 .……………………………………………………………………⑤
.……………………………………………………………………⑤
当 时,
时, ,由④⑤得,
,由④⑤得, ,将其代入⑤有
,将其代入⑤有
 .整理得
.整理得 .
.
当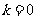 时,点
时,点 的坐标为
的坐标为 ,满足上述方程.
,满足上述方程.
当 与
与 轴垂直时,
轴垂直时, ,求得
,求得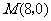 ,也满足上述方程.
,也满足上述方程.
故点 的轨迹方程是
的轨迹方程是 .
.
(II)假设在 轴上存在定点点
轴上存在定点点 ,使
,使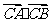 为常数,
为常数,
当 不与
不与 轴垂直时,由(I)有
轴垂直时,由(I)有 ,
,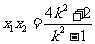 .
.
以上同解法一的(II).
(二)填空题:
7、(05浙江)过双曲线 (a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________;
(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________;
8、(05上海)若双曲线的渐近线方程为 ,它的一个焦点是
,它的一个焦点是 ,则双曲线的方程是__________。
,则双曲线的方程是__________。
(一)选择题:
1、(07全国Ⅱ)设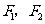 分别是双曲线
分别是双曲线 的左、右焦点,若双曲线上存在点
的左、右焦点,若双曲线上存在点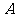 ,使
,使 且
且 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
 A、
A、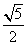 B、
B、 C、
C、 D、
D、
2、(07安徽)如图, 和
和 分别是双曲线
分别是双曲线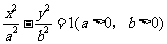
的两个焦点,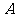 和
和 是以
是以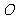 为圆心,以
为圆心,以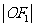 为半径的圆与
为半径的圆与
该双曲线左支的两个交点,且 是等边三角形,则双
是等边三角形,则双
曲线的离心率为( )
|
 B、
B、 C、
C、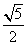 D、
D、
3、(07江苏)在平面直角坐标系 中,双曲线的中心在坐标原点,焦点在
中,双曲线的中心在坐标原点,焦点在 轴上,一条渐近线的方程为
轴上,一条渐近线的方程为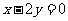 ,则它的离心率为( )
,则它的离心率为( )
A、 B、
B、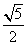 C、
C、 D、
D、
4、(07陕西)已知双曲线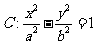 (
( ,
,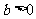 ),以
),以 的右焦点为圆心且与
的右焦点为圆心且与 的渐近线相切的圆的半径是( )
的渐近线相切的圆的半径是( )
A、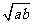 B、
B、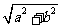 C、
C、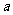 D、
D、
5、(06福建10)已知双曲线 的右焦点为
的右焦点为 ,若过点
,若过点 且倾斜角为
且倾斜角为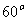 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
A、 B、
B、 C、
C、 D、
D、
6、(05全国Ⅱ)已知双曲线 的焦点为
的焦点为 、
、 ,点
,点 在双曲线上且
在双曲线上且 轴,则
轴,则 到直线
到直线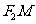 的距离为( )A、
的距离为( )A、 B、
B、 C、
C、 D、
D、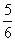
例1、(08上海春) 已知 是双曲线
是双曲线 右支上的一点,双曲线的一条渐近线方程为
右支上的一点,双曲线的一条渐近线方程为 。设
。设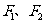 分别为双曲线的左、右焦点. 若
分别为双曲线的左、右焦点. 若 ,则
,则 ;
;
例2、(07海南) 已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为 ;
例3、(07辽宁) 设 为双曲线
为双曲线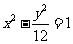 上的一点,
上的一点,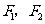 是该双曲线的两个焦点,若
是该双曲线的两个焦点,若 ,则
,则 的面积为( )
的面积为( )
A、 B、
B、 C、
C、 D、
D、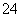
例4、(05全国Ⅲ) 已知双曲线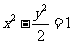 的焦点为
的焦点为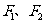 ,点
,点 在双曲线上且
在双曲线上且
 ,则点
,则点 到
到 轴的距离为( )
轴的距离为( )
A 、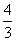 B 、
B 、 C、
C、  D、
D、
例5、(06山东21) 双曲线 与椭圆
与椭圆 有相同的热点,直线
有相同的热点,直线 =
= 为C的一条渐近线。(1)求双曲线C的方程;(2)过点
为C的一条渐近线。(1)求双曲线C的方程;(2)过点 (0,4)的直线l,求双曲线
(0,4)的直线l,求双曲线 于
于 两点,交
两点,交 轴于
轴于 点(
点( 点与
点与 的顶点不重合)。当
的顶点不重合)。当 =
=
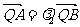 ,且
,且 时,求点
时,求点 的坐标。
的坐标。
解:(Ⅰ)设双曲线方程为 , 由椭圆
, 由椭圆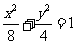
求得两焦点为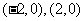 ,
, 对于双曲线
对于双曲线 ,又
,又 为双曲线
为双曲线 的一条渐近线
的一条渐近线

 解得
解得  ,
,
 双曲线
双曲线 的方程为
的方程为
(Ⅱ)解法一:
 由题意知直线
由题意知直线 的斜率
的斜率 存在且不等于零。
存在且不等于零。
设 的方程:
的方程: ,
,
则




 在双曲线
在双曲线 上,
上,






同理有:
若 则直线
则直线 过顶点,不合题意.
过顶点,不合题意.
 是二次方程
是二次方程 的两根.
的两根.

 ,
,
此时 .
.
 所求
所求 的坐标为
的坐标为 .
.
解法二:
由题意知直线 的斜率
的斜率 存在且不等于零
存在且不等于零
设 的方程,
的方程, ,则
,则 .
.
 ,
,
 分
分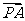 的比为
的比为 .
.
由定比分点坐标公式得

下同解法一
解法三:
由题意知直线 的斜率
的斜率 存在且不等于零
存在且不等于零
设 的方程:
的方程: ,则
,则 .
.
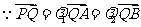 ,
,
 .
.
 ,
,
 ,
,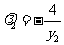 ,
,
又 ,
,

即
将 代入
代入 得
得

 ,否则
,否则 与渐近线平行。
与渐近线平行。
 。
。



解法四:
由题意知直线l得斜率k存在且不等于零,设 的方程:
的方程: ,
,
则
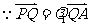 ,
,
 。
。


同理 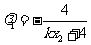
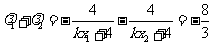 .
.
即  。 (*)
。 (*)
 又
又 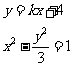
消去y得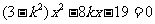 .
.
当 时,则直线l与双曲线得渐近线平行,不合题意,
时,则直线l与双曲线得渐近线平行,不合题意,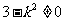 。
。
由韦达定理有:


代入(*)式得 
 所求Q点的坐标为
所求Q点的坐标为 。
。
例6、(04广东20)某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)。
解:如图,以接报中心为原点O,正东、正北方向为x轴、y轴正向,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(-1020,0),B(1020,0),C(0,1020)
设P(x,y)为巨响为生点,由A、C同时听到巨响声,得|PA|=|PB|,故P在AC的垂直平分线PO上,PO的方程为y=-x,因B点比A点晚4s听到爆炸声,故|PB|- |PA|=340×4=1360
由双曲线定义知P点在以A、B为焦点的双曲线 上,
上,
依题意得a=680, c=1020,

用y=-x代入上式,得 ,∵|PB|>|PA|,
,∵|PB|>|PA|,
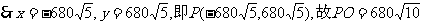
答:巨响发生在接报中心的西偏北450距中心 处。
处。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com