
(一)选择题:
1、(06北京)平面 的斜线
的斜线 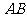 交
交 于点
于点 ,过定点
,过定点 的动直线
的动直线 与
与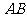 垂直,且交
垂直,且交 于点
于点 ,则动点
,则动点 的轨迹是( )
的轨迹是( )
A、一条直线 B、一个圆 C、一个椭圆 D、双曲线的一支
2、(06四川)已知两定点
 如果动点
如果动点 满足条件
满足条件 则点
则点 的轨迹所包围的图形的面积等于( )
的轨迹所包围的图形的面积等于( )
A、 B、
B、 C、
C、 D、
D、
3、(06湖北)设过点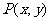 的直线分别与
的直线分别与 轴的正半轴和
轴的正半轴和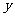 轴的正半轴交于
轴的正半轴交于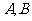 两点,点
两点,点 与点
与点 关于
关于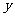 轴对称,
轴对称, 为坐标原点,若
为坐标原点,若 且
且 ,则点
,则点 的轨迹方程是 ( )
的轨迹方程是 ( )
A、 B、
B、
C、 D、
D、
4、(04辽宁6)已知点 、
、 ,动点
,动点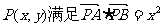 ,则点P的轨迹是( )
,则点P的轨迹是( )
A、圆 B、椭圆 C、双曲线 D、抛物线
5、(04辽宁9)已知点 、
、 ,动点
,动点 满足
满足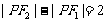 . 当点
. 当点 的纵坐标是
的纵坐标是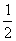 时, 点
时, 点 到坐标原点的距离是( )
到坐标原点的距离是( )
A、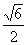 B、
B、 C、
C、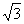 D、2
D、2
由= +得M的坐标为(x,y), 由x0,y0满足C的方程,得点M的轨迹方程为:
+ =1 (x>1,y>2)
(Ⅱ)| |2= x2+y2, y2= =4+ ,
∴| |2= x2-1++5≥4+5=9.且当x2-1= ,即x=>1时,上式取等号.
 故||的最小值为3。
故||的最小值为3。
例4、(05广东17) 在平面直角坐标系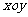 中,抛物线
中,抛物线 上异于坐标原点
上异于坐标原点 的两不同动点
的两不同动点 满足
满足 (如图4所示)(Ⅰ)求
(如图4所示)(Ⅰ)求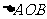 得重心
得重心 (即三角形三条中线的交点)的轨迹方程;(Ⅱ)
(即三角形三条中线的交点)的轨迹方程;(Ⅱ)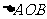 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由。
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由。
[答案]
解法一:
(Ⅰ)∵直线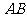 的斜率显然存在,∴设直线
的斜率显然存在,∴设直线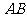 的方程为
的方程为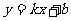 ,
,
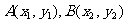 ,依题意得
,依题意得
 ,①
,①
∴ ,②
,② 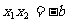 ③
③
∵ ,∴
,∴ ,即
,即  ,④
,④
由③④得, ,∴
,∴
∴设直线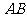 的方程为
的方程为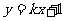
∴①可化为  ,∴
,∴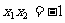 ⑤,
⑤,
设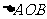 的重心G为
的重心G为 ,则
,则
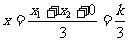 ⑥ ,
⑥ ,  ⑦,
⑦,
由⑥⑦得  ,即
,即 ,这就是
,这就是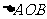 得重心
得重心 的轨迹方程.
的轨迹方程.
(Ⅱ)由弦长公式得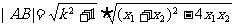
把②⑤代入上式,得  ,
,
设点 到直线
到直线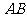 的距离为
的距离为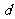 ,则
,则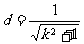 ,
,
∴ 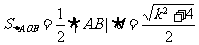 ,
,
∴ 当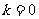 ,
,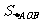 有最小值,
有最小值,
∴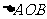 的面积存在最小值,最小值是
的面积存在最小值,最小值是 .
.
解法二:
(Ⅰ)∵ AO⊥BO, 直线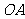 ,
, 的斜率显然存在,
的斜率显然存在,
∴设AO、BO的直线方程分别为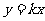 ,
, ,
,
设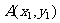 ,
,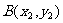 ,依题意可得
,依题意可得
由 得
得  ,由
,由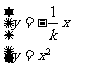 得
得 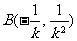 ,
,
设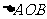 的重心G为
的重心G为 ,则
,则
 ① ,
① ,  ②,
②,
由①②可得, ,即为所求的轨迹方程.
,即为所求的轨迹方程.
(Ⅱ)由(Ⅰ)得,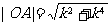 ,
,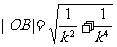 ,
,
∴

 ,
,
当且仅当 ,即
,即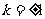 时,
时,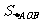 有最小值,
有最小值,
∴ 的面积存在最小值,最小值是
的面积存在最小值,最小值是 .
.
解法三:(I)设△AOB的重心为G(x , y) ,A(x1, y1),B(x2 , y2 ),则
 …(1)
…(1)
不过∵OA⊥OB ,
∴ ,即
,即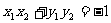 , …(2)
, …(2)
又点A,B在抛物线上,有 ,
,
代入(2)化简得 ,
,
∴ ,
,
∴所以重心为G的轨迹方程为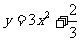 ,
,
(II)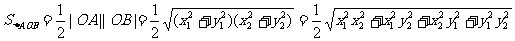 ,
,
由(I)得 ,
,
当且仅当 即
即 时,等号成立,
时,等号成立,
所以△AOB的面积存在最小值,存在时求最小值1 。
例1、(07福建20) 如图,已知点 ,
,
直线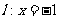 ,
, 为平面上的动点,过
为平面上的动点,过 作直线
作直线

 的垂线,垂足为点
的垂线,垂足为点 ,且
,且 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 的直线交轨迹
的直线交轨迹 于
于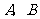 两点,交直线
两点,交直线 于点
于点 ,已知
,已知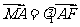 ,
, ,求
,求 的值;
的值;
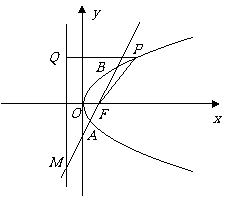 解法一:(Ⅰ)设点
解法一:(Ⅰ)设点 ,则
,则 ,由
,由 得:
得:
 ,化简得
,化简得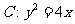 .
.
(Ⅱ)设直线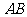 的方程为:
的方程为:
 .
.
设 ,
, ,又
,又 ,
,
联立方程组 ,消去
,消去 得:
得:
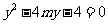 ,
, ,故
,故
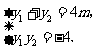
由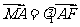 ,
, 得:
得:
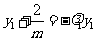 ,
, ,整理得:
,整理得:
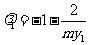 ,
, ,
,

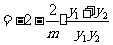

 .
.
解法二:(Ⅰ)由 得:
得: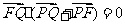 ,
,
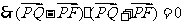 ,
,
 ,
,
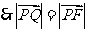 .
.
所以点 的轨迹
的轨迹 是抛物线,由题意,轨迹
是抛物线,由题意,轨迹 的方程为:
的方程为: .
.
(Ⅱ)由已知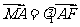 ,
, ,得
,得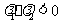 .
.
则: .…………①
.…………①
过点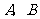 分别作准线
分别作准线 的垂线,垂足分别为
的垂线,垂足分别为 ,
, ,
,
则有: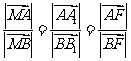 .…………②
.…………②
由①②得: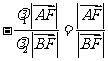 ,即
,即 .
.
例2、(06北京19) 已知点 (-2,0),
(-2,0), (2,0),动点
(2,0),动点 满足条件
满足条件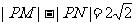 ,记动点
,记动点 的轨迹为
的轨迹为 。(Ⅰ)求
。(Ⅰ)求 的方程; (Ⅱ)若
的方程; (Ⅱ)若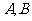 是
是 上的不同两点,
上的不同两点, 是坐标原点,求
是坐标原点,求

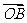 的最小值。
的最小值。
解法一:
(Ⅰ)由|PM|-|PN|= 知动点 P 的轨迹是以
知动点 P 的轨迹是以  为焦点的双曲线的右支,实
为焦点的双曲线的右支,实
半轴长
又半焦距 c=2,故虚半轴长 所以 W 的方程为
所以 W 的方程为 ,
,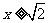
(Ⅱ)设 A,B 的坐标分别为 ,
, 
当 AB⊥x轴时,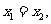 从而
从而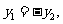 从而
从而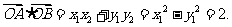 当AB与x轴不垂直时,设直线AB的方程为
当AB与x轴不垂直时,设直线AB的方程为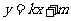 ,与W的方程联立,消去y得
,与W的方程联立,消去y得
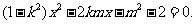 故
故
 所以
所以 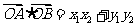




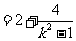 .
又因为
.
又因为 ,所以
,所以 ,从而
,从而 综上,当AB⊥
综上,当AB⊥ 轴时,
轴时, 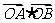 取得最小值2.
解法二:
(Ⅰ)同解法一.
取得最小值2.
解法二:
(Ⅰ)同解法一.
(Ⅱ)设 A,B 的坐标分别为,则 ,
,  ,则
,则
 令
令 则
则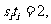 且
且 所以
所以
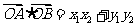
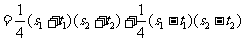
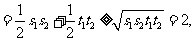 当且仅当
当且仅当 ,即
,即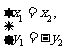 时”
时”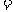 ”成立.
”成立.
所以 、
、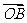 的最小值是2。
的最小值是2。
例3、(06全国Ⅰ20) 在平面直角坐标系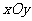 中,有一个以
中,有一个以 和
和 为焦点、离心率为
为焦点、离心率为 的椭圆,设椭圆在第一象限的部分为曲线
的椭圆,设椭圆在第一象限的部分为曲线 ,动点
,动点 在
在 上,
上, 在点
在点 处的切线与
处的切线与 轴的交点分别为
轴的交点分别为 ,且向量
,且向量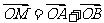 。求:(Ⅰ)点
。求:(Ⅰ)点 的轨迹方程;(Ⅱ)
的轨迹方程;(Ⅱ)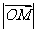 的最小值。
的最小值。
解: 椭圆方程可写为: + =1 式中a>b>0 , 且 得a2=4,b2=1,所以曲线C的方程为: x2+ =1 (x>0,y>0). y=2(0<x<1) y '=-
设P(x0,y0),因P在C上,有0<x0<1, y0=2, y '|x=x0= - ,得切线AB的方程为:
b2(x1-x2)2x+a2(y1-y2)2y=0

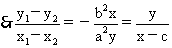
\b2x2+a2y2-b2cx=0…………(3)
2°当AB垂直于x轴时,点P即为点F,满足方程(3)
故所求点P的轨迹方程为:b2x2+a2y2-b2cx=0
(2)因为,椭圆 Q右准线l方程是x=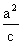 ,原点距l
,原点距l
的距离为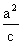 ,由于c2=a2-b2,a2=1+cosq+sinq,b2=sinq(0<q£
,由于c2=a2-b2,a2=1+cosq+sinq,b2=sinq(0<q£ )
)
则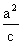 =
=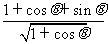 =2sin(
=2sin(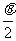 +
+ )
)
当q= 时,上式达到最大值。此时a2=2,b2=1,c=1,D(2,0),|DF|=1
时,上式达到最大值。此时a2=2,b2=1,c=1,D(2,0),|DF|=1
设椭圆Q: 上的点 A(x1,y1)、B(x2,y2),三角形ABD的面积
上的点 A(x1,y1)、B(x2,y2),三角形ABD的面积
S=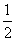 |y1|+
|y1|+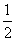 |y2|=
|y2|=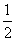 |y1-y2|
|y1-y2|
设直线m的方程为x=ky+1,代入 中,得(2+k2)y2+2ky-1=0
中,得(2+k2)y2+2ky-1=0
由韦达定理得y1+y2= ,y1y2=
,y1y2= ,
,
4S2=(y1-y2)2=(y1+y2)2-4 y1y2=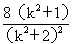
令t=k2+1³1,得4S2= ,当t=1,k=0时取等号。
,当t=1,k=0时取等号。
因此,当直线m绕点F转到垂直x轴位置时,三角形ABD的面积最大。
9、(04全国Ⅲ21)设椭圆 的两个焦点是
的两个焦点是 (
( ,0),
,0),  ,且椭圆上存在点
,且椭圆上存在点 ,使得直线
,使得直线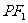 与直线
与直线 垂直. (I)求实数
垂直. (I)求实数  的取值范围;(II)设
的取值范围;(II)设 是相应于焦点
是相应于焦点 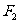 的准线,直线
的准线,直线 与
与 相交于点
相交于点 。 若
。 若 ,求直线
,求直线 的方程。
的方程。
解:⑴∵直线PF1⊥直线PF2 ∴以O为圆心以c为半径的圆:x2+y2=c2与椭圆: 有交点.即
有交点.即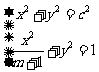 有解又∵c2=a2-b2=m+1-1=m>0
有解又∵c2=a2-b2=m+1-1=m>0
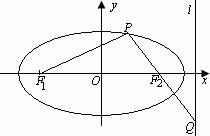 ∴
∴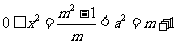 ∴
∴
⑵设P(x,y), 直线PF2方程为:y=k(x-c)
∵直线l的方程为:
∴点Q的坐标为(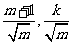 )
)
∵ ∴点P分有向线段
∴点P分有向线段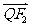 所成比为
所成比为
∵F2(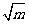 ,0),Q (
,0),Q (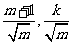 ) ∴P(
) ∴P( )
)
∵点P在椭圆上 ∴
∴
直线PF2的方程为:y=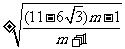 (x-
(x-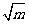 ).
).
(三)解答题:
7、(07陕西21)已知椭圆 的离心率为
的离心率为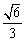 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 .
.
(Ⅰ)求椭圆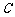 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆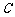 交于
交于 两点,坐标原点
两点,坐标原点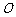 到直线
到直线 的距离为
的距离为 ,求
,求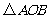 面积的最大值。
面积的最大值。
解:(Ⅰ)设椭圆的半焦距为 ,依题意
,依题意
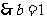 ,
,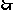 所求椭圆方程为
所求椭圆方程为 .
.
(Ⅱ)设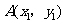 ,
,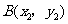 .
.
(1)当 轴时,
轴时,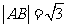 .
.
(2)当 与
与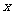 轴不垂直时,
轴不垂直时,
设直线 的方程为
的方程为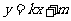 .
.
由已知 ,得
,得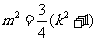 .
.
把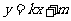 代入椭圆方程,整理得
代入椭圆方程,整理得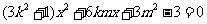 ,
,
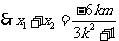 ,
, .
.
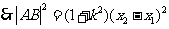
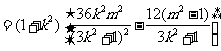

 .
.
当且仅当 ,即
,即 时等号成立.当
时等号成立.当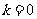 时,
时,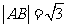 ,
,
综上所述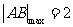 .
.
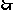 当
当 最大时,
最大时, 面积取最大值
面积取最大值 。
。
8、(06江西21)如图,椭圆 :
:  +
+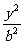 =1(
=1(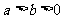 )的右焦点
)的右焦点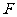
 ,过点
,过点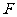
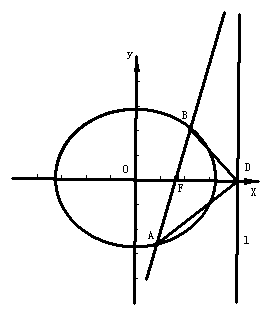 的一动直线
的一动直线 绕点
绕点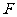 转动,并且交椭圆于
转动,并且交椭圆于 两点,
两点, 是线段
是线段 的中点
的中点
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)在 的方程中,令
的方程中,令 ,
,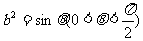 ,确定
,确定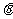 的值,使原点距椭圆的右准线
的值,使原点距椭圆的右准线 最远,此时,设
最远,此时,设 与x轴交点为
与x轴交点为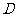 ,当直线
,当直线 绕点
绕点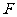 转动到什么位置时,三角形
转动到什么位置时,三角形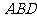 的面积最大?
的面积最大?
解:如图,(1)设椭圆Q: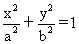 (a>b>0)
(a>b>0)
上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),则

1°当AB不垂直x轴时,x1¹x2,
(二)填空题:
4、(07福建)已知正方形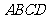 ,则以
,则以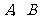 为焦点,且过
为焦点,且过 两点的椭圆的离心率为______;
两点的椭圆的离心率为______;
5、(07江苏)在平面直角坐标系 中,已知
中,已知 的顶点
的顶点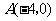 和
和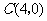 ,顶点
,顶点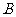 在椭圆
在椭圆 上,则
上,则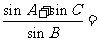 _____;
_____;
6、(06上海)已知椭圆中心在原点,一个焦点为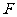 (-2
(-2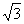 ,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
(一)选择题:
1、(06全国Ⅱ)已知△ 的顶点
的顶点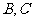 在椭圆
在椭圆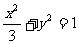 上,顶点
上,顶点 是椭圆的一个焦点,且椭圆的另外一个焦点在
是椭圆的一个焦点,且椭圆的另外一个焦点在 边上,则△
边上,则△ 的周长是( )
的周长是( )
A、2 B、6 C、4 D、12
2、(06辽宁)曲线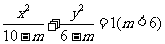 与曲线
与曲线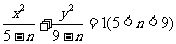 的
的
A、焦距相等 B、离心率相等 C、焦点相同 D、准线相同
3、(05广东)若焦点在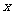 轴上的椭圆
轴上的椭圆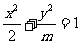 的离心率为
的离心率为 ,则
,则 ( )
( )
A、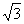 B、
B、 C、
C、 D、
D、
例1、(08上海春)已知椭圆 ,长轴在
,长轴在 轴上. 若焦距为
轴上. 若焦距为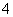 ,则
,则 等于 ( )
等于 ( )
A、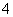 B、
B、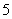 C、
C、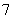 D、
D、
例2、(07山东21)已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在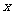 轴上,椭圆
轴上,椭圆 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为 ,最小值为
,最小值为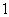 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若直线 与椭圆
与椭圆 相交于
相交于 ,
,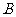 两点(
两点(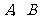 不是左、右顶点),且以
不是左、右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标。
过定点,并求出该定点的坐标。
解:(Ⅰ)由题意设椭圆的标准方程为 ,
,
由已知得: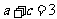 ,
,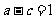 ,
,
 ,
, ,
,
 .
.
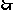 椭圆的标准方程为
椭圆的标准方程为 .
.
(Ⅱ)设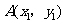 ,
,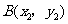 ,
,
联立
得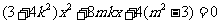 ,
,

又 ,
,
因为以 为直径的圆过椭圆的右焦点
为直径的圆过椭圆的右焦点 ,
,
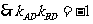 ,即
,即 ,
,
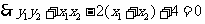 ,
,
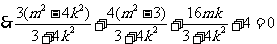 ,
,
 .
.
解得:
 ,
,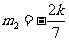 ,且均满足
,且均满足 ,
,
当 时,
时, 的方程为
的方程为 ,直线过定点
,直线过定点 ,与已知矛盾;
,与已知矛盾;
当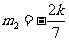 时,
时, 的方程为
的方程为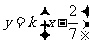 ,直线过定点
,直线过定点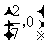 .
.
所以,直线 过定点,定点坐标为
过定点,定点坐标为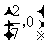 .
.
例3、(07上海春18)如图,在直角坐标系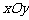 中,设椭圆
中,设椭圆

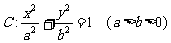 的左右两个焦点分别为
的左右两个焦点分别为
 过右焦点
过右焦点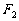 且与
且与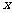 轴垂直的直线
轴垂直的直线 与椭圆
与椭圆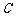 相交,其中一个交点为
相交,其中一个交点为
 (1) 求椭圆
(1) 求椭圆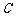 的方程;
的方程;
(2) 设椭圆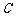 的一个顶点为
的一个顶点为 ,直线
,直线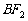 交椭圆
交椭圆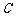 于另一点
于另一点 ,求△
,求△ 的面积。
的面积。
(1) [解法一]  轴,
轴, 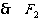 的坐标为
的坐标为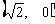
 …… 2分
…… 2分
 由题意可知
由题意可知  得
得 
 所求椭圆方程为
所求椭圆方程为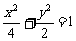
 …… 6分
…… 6分
[解法二]由椭圆定义可知

 由题意
由题意 ,
,
 …… 2分
…… 2分
又由 △
△ 可知
可知  ,
, ,
,
 ,又
,又 ,得
,得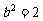

 椭圆
椭圆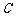 的方程为
的方程为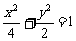
 …… 6分
…… 6分
[解] (2) 直线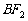 的方程为
的方程为
 …… 8分
…… 8分
由 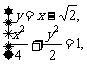 得点
得点 的纵坐标为
的纵坐标为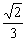
 …… 10分
…… 10分
又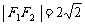 ,
,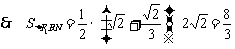
 …… 14分
…… 14分
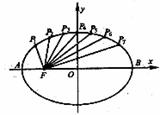 例4、(06四川)如图把椭圆
例4、(06四川)如图把椭圆 的长轴
的长轴 分成8分,过每个分点作
分成8分,过每个分点作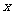 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于 ,
, ,……
,……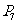 七个点,
七个点,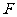 是椭圆的一个焦点,则
是椭圆的一个焦点,则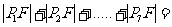 ____________.
____________.
例5、(05全国Ⅲ)设椭圆的两个焦点分别为 ,过
,过 作椭圆长轴的垂线交椭圆于点
作椭圆长轴的垂线交椭圆于点 ,若
,若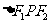 为等腰直角三角形,则椭圆的离心率为( )
为等腰直角三角形,则椭圆的离心率为( )
A、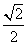 B、
B、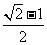 C、
C、 D、
D、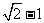
 例6、(05上海19)如图,点
例6、(05上海19)如图,点 、
、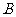 分别是椭圆
分别是椭圆 长轴的左、右端点,点
长轴的左、右端点,点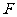 是椭圆的右焦点,点
是椭圆的右焦点,点 在椭圆上,且位于
在椭圆上,且位于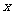 轴上方,
轴上方, .(1)求点
.(1)求点 的坐标;(2)设
的坐标;(2)设 是椭圆长轴
是椭圆长轴 上的一点,
上的一点, 到直线
到直线 的距离等于
的距离等于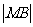 ,求椭圆上的点到点
,求椭圆上的点到点 的距离
的距离 的最小值.
的最小值.
[解](1)由已知可得点A(-6,0),F(4,0)
设点P的坐标是 ,由已知得
,由已知得
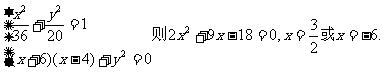
由于
(2)直线AP的方程是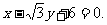
设点M的坐标是(m,0),则M到直线AP的距离是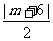 ,
,
于是
椭圆上的点 到点M的距离d有
到点M的距离d有

由于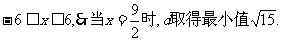
例7、(05湖南19)已知椭圆 :
: +
+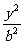 =1(
=1(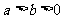 )的左.右焦点为
)的左.右焦点为 ,离心率为
,离心率为 . 直线
. 直线 与
与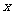 轴.
轴. 轴分别交于点
轴分别交于点 ,
, 是直线
是直线 与椭圆
与椭圆 的一个公共点,
的一个公共点, 是点
是点 关于直线
关于直线 的对称点,设
的对称点,设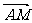 =
=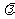
 。(Ⅰ)证明:
。(Ⅰ)证明: ;(Ⅱ)确定
;(Ⅱ)确定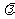 的值,使得
的值,使得 是等腰三角形。
是等腰三角形。
(Ⅰ)证法一:因为A、B分别是直线l: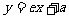 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是 .
.
所以点M的坐标是( ). 由
). 由
即
证法二:因为A、B分别是直线l: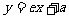 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是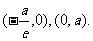 设M的坐标是
设M的坐标是
所以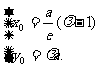 因为点M在椭圆上,所以
因为点M在椭圆上,所以 
即
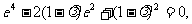 解得
解得
(Ⅱ)解法一:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,即
设点F1到l的距离为d,由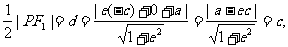
得 所以
所以
即当 △PF1F2为等腰三角形.
△PF1F2为等腰三角形.
解法二:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,
设点P的坐标是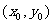 ,
,
则
由|PF1|=|F1F2|得
两边同时除以4a2,化简得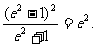 从而
从而
于是 . 即当
. 即当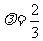 时,△PF1F2为等腰三角形。
时,△PF1F2为等腰三角形。
(三)解答题:
11、(07安徽)如图,曲线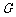 的方程为
的方程为 .以原点为圆心.以
.以原点为圆心.以 为半径的圆分别与曲线
为半径的圆分别与曲线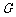 和
和 轴的正半轴相交于点
轴的正半轴相交于点 与点
与点 .直线
.直线 与
与 轴相交于点
轴相交于点 .
.
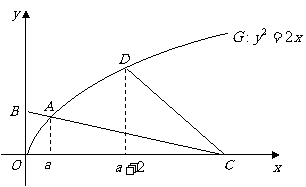 (Ⅰ)求点
(Ⅰ)求点 的横坐标
的横坐标 与点
与点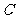 的横坐标
的横坐标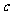 的关系式;(Ⅱ)设曲线
的关系式;(Ⅱ)设曲线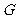 上点
上点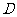 的横坐标为
的横坐标为 ,
,
求证:直线 的斜率为定值。
的斜率为定值。
|
12、(06上海春)学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为 ,变轨(即航天器运行轨迹由椭圆变为
,变轨(即航天器运行轨迹由椭圆变为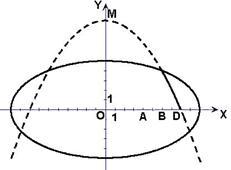 抛物线)后返回的轨迹是以
抛物线)后返回的轨迹是以 轴为对称轴、
轴为对称轴、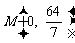 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为 。观测点
。观测点 同时跟踪航天器。
同时跟踪航天器。
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在 轴上方时,观测点
轴上方时,观测点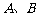 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
[解](1)设曲线方程为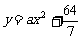 , 由题意可知,
, 由题意可知, .
.  .
……4分
.
……4分
 曲线方程为
曲线方程为 .
……6分
.
……6分
 (2)设变轨点为
(2)设变轨点为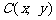 ,根据题意可知
,根据题意可知
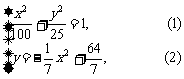 得
得  ,
,
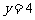 或
或 (不合题意,舍去).
(不合题意,舍去).
 .
……9分
.
……9分
得
 或
或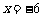 (不合题意,舍去).
(不合题意,舍去). 
 点的坐标为
点的坐标为 ,
……11分
,
……11分
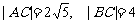 .
.
答:当观测点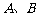 测得
测得 距离分别为
距离分别为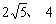 时,应向航天器发出变轨指令。
……14分
时,应向航天器发出变轨指令。
……14分
13、(04全国Ⅱ21)给定抛物线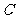 :
: ,
,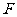 是
是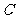 的焦点,过点
的焦点,过点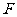 的直线
的直线 与
与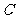 相交于
相交于 两点.(Ⅰ)设
两点.(Ⅰ)设 的斜率为1,求
的斜率为1,求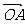 与
与 夹角的大小;(Ⅱ)设
夹角的大小;(Ⅱ)设 =
= ,若
,若 ∈[4,9],求
∈[4,9],求 在
在 轴上截距的变化范围。
轴上截距的变化范围。
解:(I)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为y=x-1.
将y=x-1代入方程y2=4x,并整理得x2-6x+1=0.
设A(x1,y1),B(x2,y2),则有x1+x2=6,x1x2=1,
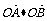 =(x1,y1)·(x2,y2)=x1x2+y1y2=2x1x2-(x1+x2)+1=-3.
=(x1,y1)·(x2,y2)=x1x2+y1y2=2x1x2-(x1+x2)+1=-3.

cos<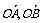 >=
>=
所以 与
与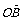 夹角的大小为
夹角的大小为 -arccos
-arccos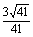 。
。
解:(II)由题设知 得:(x2-1,y2)=λ(1-x1,-y1),即
得:(x2-1,y2)=λ(1-x1,-y1),即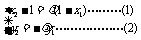
由 (2)得y22=λ2y12, ∵y12=4x1,y22=4x2,∴x2=λ2x1 ……………………………………(3)
……………………………………(3)
联立(1)(3)解得x2=λ.依题意有λ>0.
∴B(λ,2 )或B(λ,-2
)或B(λ,-2 ),又F(1,0),
),又F(1,0),
得直线l的方程为(λ-1)y=2 (x-1)或(λ-1)y=-2
(x-1)或(λ-1)y=-2 (x-1)
(x-1)
当λ∈[4,9]时,l在y轴上的截距为 或-
或-

由 =
= ,可知
,可知 在[4,9]上是递减的,
在[4,9]上是递减的,
∴

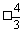 ,-
,- -
-


直线l在y轴上截距的变化范围是 。
。
(二)填空题:
8、(07广东)在平面直角坐标系 中,有一定点
中,有一定点 ,若线段
,若线段 的垂直平分线过抛物线
的垂直平分线过抛物线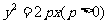 的焦点,则该抛物线的准线方程是
;
的焦点,则该抛物线的准线方程是
;
9、(06福建)已知直线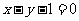 与抛物线
与抛物线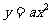 相切,则
相切,则
10、(05重庆16)连接抛物线上任意四点组成的四边形可能是 (填写所有正确选项的序号)。①菱形 ②有3条边相等的四边形 ③梯形 ④平行四边形 ⑤有一组对角相等的四边形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com