
5、在数列{an}中,a1=1,当n≥2时,  ,且已知此数列有极限,则
,且已知此数列有极限,则 等于( )
等于( )
A、-2 B、-1 C、0 D、1
4、已知y=f(x)=ln|x|, 则下列各命题中,正确的命题是…………………………………………( )
A、x>0时,
B、x>0时,
C、x≠0时,都有
D、∵x=0时f(x)无意义, ∴对y=ln(x)不能求导;
3、与直线2x-y+4=0平行的抛物线y=x2的切线方程是…………………………………………( )
A、2x-y+3=0 B、2x-y-3=0 C、2x-y+1=0 D、2x-y-1=0
2、①若在点x0处连续,则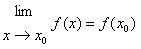
②函数f(x)在点x0处有定义,则函数在x0处连续
③函数f(x), g(x)在某一点x=x0处连续,则 在x=x0处连续;
在x=x0处连续;
④若f(x)在(a, b)内连续,则在该区间内必能取得最大值和最小值,其中正确的有……( )
A、1个 B、2个 C、3个 D、4个
1、满足条件|z-i|=|3+4i|的复数z在复平面内对应的轨迹是…………………………………( )
A、一条直线 B、两条直线 C、圆 D、椭圆
(二)填空题:
4、(07重庆16)过双曲线 的右焦点
的右焦点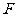 作倾斜角为
作倾斜角为 的直线,交双曲线于
的直线,交双曲线于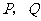 两点,则
两点,则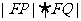 的值为______;
的值为______;
5、(06上海)若曲线 =|
=| |+1与直线
|+1与直线 =
= +
+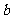 没有公共点,则
没有公共点,则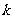 、
、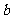 分别应满足的条件是 ;
分别应满足的条件是 ;
6、(06山东)已知抛物线 ,过点
,过点 的直线与抛物线相交于
的直线与抛物线相交于 两点,则
两点,则 的最小值是
;
的最小值是
;
7、(04重庆16)对任意实数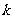 ,直线
,直线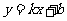 与椭圆:
与椭圆: 恰有一个公共点,则
恰有一个公共点,则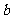 取值范围是_______________。
取值范围是_______________。
 (三)解答题:
(三)解答题:
8、(07江苏19)如图,在平面直角坐标系 中,过
中,过 轴正方向上一点
轴正方向上一点 任作一直线,与抛物线
任作一直线,与抛物线 相交于
相交于 两点.一条垂直于
两点.一条垂直于 轴的直线,分别与线段
轴的直线,分别与线段 和直线
和直线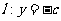 交于点
交于点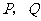 。
。
(1)若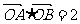 ,求
,求 的值;(5分)
的值;(5分)
(2)若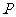 为线段
为线段 的中点,求证:
的中点,求证: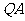 为此抛物线的切线;(5分)
为此抛物线的切线;(5分)
(3)试问(2)的逆命题是否成立?说明理由。(4分)
 解:(1)设直线
解:(1)设直线 的方程为
的方程为 ,
,
将该方程代入 得
得 .
.
令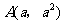 ,
,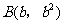 ,则
,则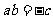 .
.
因为 ,解得
,解得 ,
,
或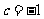 (舍去).故
(舍去).故 .
.
(2)由题意知 ,直线
,直线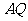 的斜率为
的斜率为 .
.
又 的导数为
的导数为 ,所以点
,所以点 处切线的斜率为
处切线的斜率为 ,
,
因此,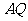 为该抛物线的切线.
为该抛物线的切线.
(3)(2)的逆命题成立,证明如下:
设 .
.
若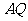 为该抛物线的切线,则
为该抛物线的切线,则 ,
,
又直线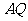 的斜率为
的斜率为 ,所以
,所以 ,
,
得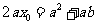 ,因
,因 ,有
,有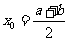 .
.
故点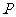 的横坐标为
的横坐标为 ,即
,即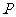 点是线段
点是线段 的中点.
的中点.
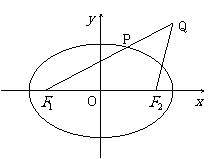
9、(07四川20)设 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点.
(Ⅰ)若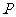 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求 ·
·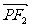 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点 的直线
的直线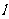 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且∠
,且∠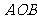 为锐角(其中
为锐角(其中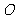 为坐标原点),求直线
为坐标原点),求直线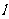 的斜率
的斜率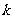 的取值范围。
的取值范围。
解:(Ⅰ)解法一:易知
所以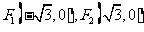 ,设
,设 ,则
,则


因为 ,故当
,故当 ,即点
,即点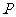 为椭圆短轴端点时,
为椭圆短轴端点时, 有最小值
有最小值
当 ,即点
,即点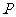 为椭圆长轴端点时,
为椭圆长轴端点时, 有最大值
有最大值
解法二:易知 ,所以
,所以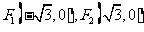 ,设
,设 ,则
,则
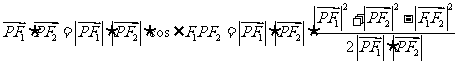
 (以下同解法一)
(以下同解法一)
(Ⅱ)显然直线 不满足题设条件,可设直线
不满足题设条件,可设直线 ,
,
联立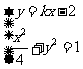 ,消去
,消去 ,整理得:
,整理得:
∴
由 得:
得: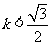 或
或
又
∴
又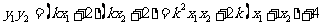
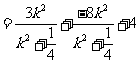

∵ ,即
,即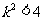 ∴
∴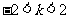
故由①、②得 或
或
10、(07全国Ⅰ)已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,
, .过
.过 的直线交椭圆于
的直线交椭圆于 两点,过
两点,过 的直线交椭圆于
的直线交椭圆于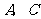 两点,且
两点,且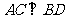 ,垂足为
,垂足为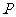 .
.
(Ⅰ)设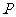 点的坐标为
点的坐标为 ,证明:
,证明: ;
;
(Ⅱ)求四边形 的面积的最小值。
的面积的最小值。
(Ⅰ)椭圆的半焦距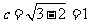 ,
,
由 知点
知点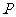 在以线段
在以线段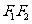 为直径的圆上,故
为直径的圆上,故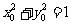 ,
,
所以, .
.
(Ⅱ)(ⅰ)当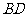 的斜率
的斜率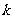 存在且
存在且 时,
时,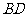 的方程为
的方程为 ,代入椭圆方程
,代入椭圆方程 ,并化简得
,并化简得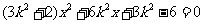 .
.
设 ,
, ,则
,则
 ,
,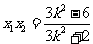
 ;
;
因为 与
与 相交于点
相交于点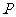 ,且
,且 的斜率为
的斜率为 ,
,
所以, .
.
四边形 的面积
的面积
 .
.
当 时,上式取等号.
时,上式取等号.
(ⅱ)当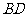 的斜率
的斜率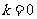 或斜率不存在时,四边形
或斜率不存在时,四边形 的面积
的面积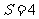 .
.
综上,四边形 的面积的最小值为
的面积的最小值为 .
.
11、 (06浙江)如图,椭圆
(06浙江)如图,椭圆
 与过点
与过点 的直线有且只有一个公共点
的直线有且只有一个公共点 ,且椭圆的离心率
,且椭圆的离心率
 .(Ⅰ)求椭圆方程;(Ⅱ)设
.(Ⅰ)求椭圆方程;(Ⅱ)设 分别为椭圆的左、右焦点,
分别为椭圆的左、右焦点, 为线段
为线段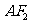 的中点,求证:
的中点,求证: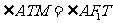 。
。
解:(I)过点 、
、 的直线方程为
的直线方程为
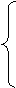

因为由题意得 有惟一解,
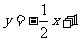
即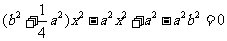 有惟一解,
有惟一解,
所以
 (
(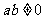 ),
),
故 
又因为  即
即 
所以 
从而得 
故所求的椭圆方程为 
(II)由(I)得 
故
从而


由
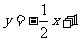
解得
所以 
因为
又
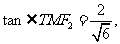 得
得

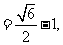
因此
(一)选择题:
1、(06天津10)直线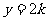 与曲线
与曲线 的公共点的个数为( )D
的公共点的个数为( )D
A、1 B、2 C、3 D、4
2、(05山东)设直线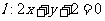 关于原点对称的直线为
关于原点对称的直线为 ,若
,若 与椭圆
与椭圆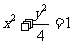 的交点为
的交点为 ,点
,点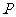 为椭圆上的动点,则使
为椭圆上的动点,则使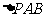 的面积为
的面积为 的点
的点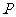 的个数为( )
的个数为( )
A、1 B、2 C、3 D、4
3、(04福建)已知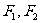 是椭圆的两个焦点,过
是椭圆的两个焦点,过 且与椭圆长轴垂直的直线交椭圆于
且与椭圆长轴垂直的直线交椭圆于 两点,若△
两点,若△ 是正三角形,则这个椭圆的离心率是( )
是正三角形,则这个椭圆的离心率是( )
A、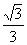 B、
B、 C、
C、 D、
D、
例1、(07四川) 已知抛物线 上存在关于直线
上存在关于直线 对称的相异两点A、B,则|AB|等于( )
对称的相异两点A、B,则|AB|等于( )
A、3 B、4 C、 D、
D、
例2、(07海南19)在平面直角坐标系 中,经过点
中,经过点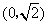 且斜率为
且斜率为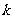 的直线
的直线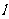 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点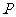 和
和 .
.
(I)求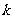 的取值范围;
的取值范围;
(II)设椭圆与 轴正半轴、
轴正半轴、 轴正半轴的交点分别为
轴正半轴的交点分别为 ,是否存在常数
,是否存在常数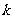 ,使得向量
,使得向量 与
与 共线?如果存在,求
共线?如果存在,求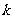 值;如果不存在,请说明理由。
值;如果不存在,请说明理由。
例3、(06天津22)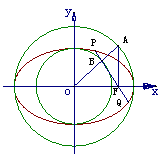 如图,以椭圆
如图,以椭圆 的中心
的中心 为圆心,分别以
为圆心,分别以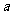 和
和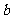 为半径作大圆和小圆
为半径作大圆和小圆 过椭圆右焦点
过椭圆右焦点 作垂直于
作垂直于 轴的直线交大圆于第一象限内的点
轴的直线交大圆于第一象限内的点 .连结
.连结 交小圆于点
交小圆于点 .设直线
.设直线 是小圆的切线.
是小圆的切线.
(1)证明: ,并求直线
,并求直线 与
与 轴的交点
轴的交点 的坐标;
的坐标;
(2)设直线 交椭圆于
交椭圆于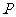 ,
, 两点,证明
两点,证明 。
。
(Ⅰ)由题设条件知,Rt△OFA∽Rt△OBF 故 ,即
,即 故
故 ,在Rt△OFA中
,在Rt△OFA中 
直线OA的斜率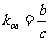 .
.
设直线BF的斜率为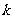 ,则
,则 .
.
直线BF与 轴的交点为
轴的交点为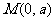

(Ⅱ)由(Ⅰ),得直线BF得方程为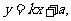
 且
且
设 、
、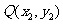 ,
,
由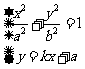 得
得

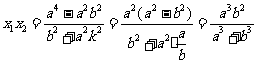
由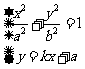 得
得
 ⑤
⑤


注意到 ,得
,得
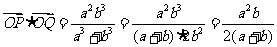

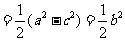 。
。
例4、(05全国Ⅱ21)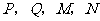 四点都在椭圆
四点都在椭圆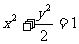 上,
上,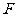 为椭圆在
为椭圆在 轴正半轴上的焦点.已知
轴正半轴上的焦点.已知 与
与 共线,
共线, 与
与 共线,且
共线,且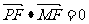 .求四边形
.求四边形 的面积的最小值和最大值.
的面积的最小值和最大值.
(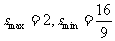 )
)
例5、(05全国Ⅰ21)已知椭圆的中心为坐标原点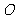 ,焦点在
,焦点在 轴上,斜率为1且过椭圆右焦点
轴上,斜率为1且过椭圆右焦点 的直线交椭圆于
的直线交椭圆于 两点,
两点, 与
与 共线。
共线。
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且 ,证明
,证明 为定值。
为定值。
(三)解答题:
7、(06江苏17)已知三点 (5,2)、
(5,2)、 (-6,0)、
(-6,0)、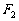 (6,0)。(Ⅰ)求以
(6,0)。(Ⅰ)求以 、
、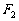 为焦点且过点
为焦点且过点 的椭圆的标准方程;(Ⅱ)设点
的椭圆的标准方程;(Ⅱ)设点 、
、 、
、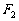 关于直线
关于直线 的对称点分别为
的对称点分别为 、
、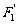 、
、 ,求以
,求以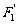 、
、 为焦点且过点
为焦点且过点 的双曲线的标准方程。
的双曲线的标准方程。
8、(06广东18)设函数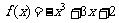 分别在
分别在 处取得极小值、极大值.
处取得极小值、极大值. 平面上点
平面上点 的坐标分别为
的坐标分别为 、
、 ,该平面上动点
,该平面上动点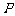 满足
满足 ,点
,点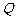 是点
是点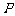 关于直线
关于直线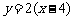 的对称点。求(I)求点
的对称点。求(I)求点 的坐标;(II)求动点
的坐标;(II)求动点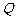 的轨迹方程。
的轨迹方程。
9、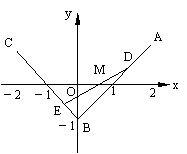 (06陕西21)如图,三定点
(06陕西21)如图,三定点 (2,1),
(2,1), (0,-1),
(0,-1), (-2,1);三动点
(-2,1);三动点 满足
满足 ,
, ,
,  ,
, 。(Ⅰ) 求动直线
。(Ⅰ) 求动直线 斜率的变化范围;(Ⅱ)求动点
斜率的变化范围;(Ⅱ)求动点 的轨迹方程。
的轨迹方程。
解法一: 如图, (Ⅰ)设D(x0,y0),E(xE,yE),M(x,y).由=t, = t , 知(xD-2,yD-1)=t(-2,-2). ∴ 同理 . ∴kDE = = = 1-2t.
∴t∈[0,1] , ∴kDE∈[-1,1].
(Ⅱ) ∵=t ∴(x+2t-2,y+2t-1)=t(-2t+2t-2,2t-1+2t-1)=t(-2,4t-2)=(-2t,4t2-2t). ∴ , ∴y= , 即x2=4y. ∵t∈[0,1], x=2(1-2t)∈[-2,2].
即所求轨迹方程为: x2=4y, x∈[-2,2]
解法二: (Ⅰ)同上.
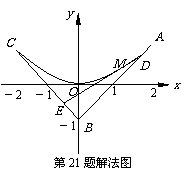 (Ⅱ) 如图, =+ = + t
= + t(-) = (1-t) +t,
(Ⅱ) 如图, =+ = + t
= + t(-) = (1-t) +t,
= + = +t = +t(-) =(1-t) +t,
= += + t= +t(-)=(1-t) + t
= (1-t2) + 2(1-t)t+t2 .
设M点的坐标为(x,y),由=(2,1), =(0,-1), =(-2,1)得
消去t得x2=4y, ∵t∈[0,1], x∈[-2,2].
故所求轨迹方程为: x2=4y, x∈[-2,2]。
10、(05江西22)如图,设抛物线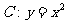 的焦点为
的焦点为 ,动点
,动点 在直线
在直线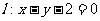 上运动,过
上运动,过 作抛物线
作抛物线 的两条切线
的两条切线 ,且与抛物线
,且与抛物线 分别相切于
分别相切于 两点。
两点。
(1)求△ 的重心
的重心 的轨迹方程;
的轨迹方程;
(2)证明: 。
。
[思路点拨]本题涉及解析几何中直线与抛物线的若干知识.
[正确解答](1)设切点A、B坐标分别为 ,
,
∴切线AP的方程为:
切线BP的方程为:
解得P点的坐标为:
所以△APB的重心G的坐标为 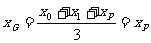 ,
,
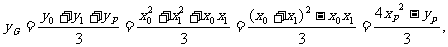
所以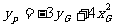 ,由点P在直线l上运动,从而得到重心G的轨迹方程为:
,由点P在直线l上运动,从而得到重心G的轨迹方程为:

(2)方法1:因为
由于P点在抛物线外,则
∴
同理有
∴∠AFP=∠PFB.
方法2:①当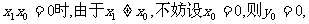 所以P点坐标为
所以P点坐标为 ,则P点到直线AF的距离为:
,则P点到直线AF的距离为:

即
所以P点到直线BF的距离为:
所以d1=d2,即得∠AFP=∠PFB.
②当 时,直线AF的方程:
时,直线AF的方程: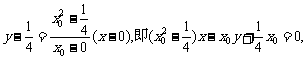
直线BF的方程:
所以P点到直线AF的距离为:
 ,同理可得到P点到直线BF的距离
,同理可得到P点到直线BF的距离 ,因此由d1=d2,可得到∠AFP=∠PFB.
,因此由d1=d2,可得到∠AFP=∠PFB.
[解后反思]解析几何主要的是点和曲线的位置关系、对称性,标准方程当中系数对位置的影响.圆锥曲线的定义和几何性质,解析几何的解答题往往是高档题,常常涉及的内容是求轨迹方程、直线和圆锥曲线的位置关系、对称、最值、范围.做这类题目一定要认真细心,提高自己的运算能力和思维能力。
11、(05辽宁21)已知椭圆 的左、右焦点分别是
的左、右焦点分别是 、
、 ,
, 是椭圆外的动点,满足
是椭圆外的动点,满足 ,点
,点 是线段
是线段 与该椭圆的交点,点
与该椭圆的交点,点 在线段
在线段 上,并且满足
上,并且满足 。(Ⅰ)设
。(Ⅰ)设 为点
为点 的横坐标,证明
的横坐标,证明  ;(Ⅱ)求点
;(Ⅱ)求点 的轨迹
的轨迹 的方程;(Ⅲ)试问:在点
的方程;(Ⅲ)试问:在点 的轨迹
的轨迹 上,是否存在点
上,是否存在点 ,使△
,使△ 的面积
的面积 .若存在,求∠
.若存在,求∠ 的正切值;若不存在,请说明理由。
的正切值;若不存在,请说明理由。
 分析:本小题主要考查平面向量的概率,椭圆的定义、标准方程和有关性质,轨迹的求法和应
分析:本小题主要考查平面向量的概率,椭圆的定义、标准方程和有关性质,轨迹的求法和应
用,以及综合运用数学知识解决问题的能力.满分14分.
(Ⅰ)证法一:设点P的坐标为
 由P
由P 在椭圆上,得
在椭圆上,得

由 ,所以
,所以  ……3分
……3分
证法二:设点P的坐标为 记
记
则
由 ,得
,得
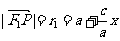 .
.
证法三:设点P的坐标为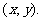
椭圆的左准线方程为
由椭圆第二定义得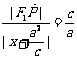 ,即
,即
由 ,所以
,所以 ……3分
……3分
(Ⅱ)解法一:设点T的坐标为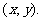
当 时,点(
时,点(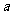 ,0)和点(-
,0)和点(-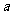 ,0)在轨迹上.
,0)在轨迹上.
当| 时,
时,
由 ,得
,得 .
.
又 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
在△QF1F2中,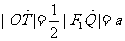 ,所以有
,所以有
综上所述,点T的轨迹C的方程是 ……7分
……7分
解法二:设点T的坐标为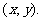 当
当 时,点(
时,点(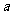 ,0)和点(-
,0)和点(-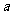 ,0)在轨迹上.
,0)在轨迹上.
当| 时,由
时,由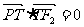 ,得
,得 .
.
又 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
设点Q的坐标为(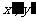 ),则
),则
因此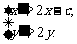 ①
①
由 得
得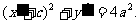 ②
②
将①代入②,可得
综上所述,点T的轨迹C的方程是 ……7分
……7分
|
 )使S=
)使S= 的充要条件是
的充要条件是

由③得 ,
,
由④得
所以,当 时,存在点M,使S=
时,存在点M,使S= ;
;
当 时,不存在满足条件的点M. ……11分
时,不存在满足条件的点M. ……11分
当 时,
时, ,
,
由 ,
,
 ,
,
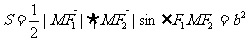 ,得
,得

解法二:
C上存在点M( )使S=
)使S= 的充要条件是
的充要条件是
|

由④得 上式代入③得
上式代入③得

于是,当 时,存在点M,使S=
时,存在点M,使S= ;
;
当 时,不存在满足条件的点M. ……11分
时,不存在满足条件的点M. ……11分
当 时,记
时,记 ,
,
由 知
知 ,所以
,所以
 ……14分
……14分
(二)填空题:
6、(07四川)已知⊙ 的方程是
的方程是 ,⊙
,⊙ 的方程是
的方程是 ,由动点
,由动点 向⊙
向⊙ 和⊙
和⊙ 所引的切线长相等,则动点
所引的切线长相等,则动点 的轨迹方程是
。
的轨迹方程是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com