
5. 下列句子中,有语病的一句是( )
A. 现在,基层一些地方政府报的GDP数字,大都是在年初既定的数字上再加一点报上去的。
B. 教育评估的目的主要是基础检查,是对学校是否达标的评估,而不应该成为一种功利性的“锦上添花”。
C. 眼前被沙尘暴刮倒的云杉、干涸的河道、大片的沙漠难道不是成吉思汗留给他的子民们的遗产么?
D. 1999年7月李登辉抛出“两国论”后,海基会与海协会酝酿汪道涵先生访台的计划告吹。
4. 下列句子中,加点成语使用恰当的一句是( )
A. 我与同事们一直保持中距离,不偏不倚,不太疏远,也不靠得太近,这样更有利于工作。
B. 台湾当局“一边一国”的错误言论导致台湾股市下跌,也引起了台湾人民的怨声载道。
C. 教育孩子决不能简单粗暴,那种动辄拳脚相加、耳提面命的做法,只能得到相反的效果。
D. 对您这篇文章中所谈的问题,我深有同感,忍不住在后面加了几句话,就算狗尾续貂吧。
3. 下列依次填入横线处的词语,恰当的一组是( )
古代书法家的队伍很大,层次很多,就我见闻所及,当代一些书法高手完全有资格与古代的一些书法家一比高低。_______________,一个无法比拟的先决条件是,古代书法家是以一种极其广阔的社会必需性为背景,______________产生得特别自然、随便、诚恳;而当代书法终究是一条刻意维修的幽径,美则美矣,_______________未免失去了整体上的社会性诚恳。
A. 但是 当然 也
B. 但是 因而 却
C. 诚然 所以 却
D. 因为 所以 也
2. 下列各组词语中,没有错别字的一组是( )
A. 胁迫 度假 貌合神离 坐收渔利
B. 凋敝 嬗变 不纠既往 金碧辉煌
C. 事态 辍泣 墨守成规 反璞归真
D. 沉缅 收讫 人才倍出 拾遗补阙
1. 下列各组词语中,加点的字读音全都相同的一项是( )
A. 绮梦幻想 椅子 倚靠 旖旎
B. 居心叵测 倨傲 盘踞 拮据
C. 鞠躬尽瘁 荟萃 淬火 仓猝
D. 脸颊红润 夹袄 长铗 豆荚
10. 如图,已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点,
 ⑴如果
⑴如果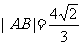 ,求直线MQ的方程;
,求直线MQ的方程;
⑵求动弦AB的中点P的轨迹方程.
解:⑴解(1)由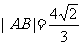 可得
可得

由射影定理得 在Rt△MOQ中,
在Rt△MOQ中,
 ,
,
故 ,所以直线AB方程是
,所以直线AB方程是
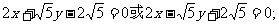
⑵连接MB,MQ,设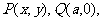 由点M,P,Q在一直线上,得
由点M,P,Q在一直线上,得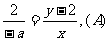
由射影定理得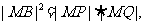 即
即
把(A)及(B)消去a,并注意到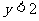 ,可得
,可得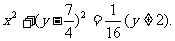
[探索题]已知圆的方程是:x2+y2-2ax+2(a-2)y+2=0,其中a≠1,且a∈R。
(1)求证:a取不为1的实数时,上述圆恒过定点;
(2)求与圆相切的直线方程;
(3)求圆心的轨迹方程。
解:将方程x2+y2-2ax+2(a-2)y+2=0整理得x2+y2-4y+2-a(2x-2y)=0
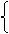 令
x2+y2-4y+2=0
令
x2+y2-4y+2=0
x-y=0
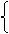 解之得
x=1
解之得
x=1
y=1
∴定点为(1,1)
(2)易得已知圆的圆心坐标为(a,2-a),半径为 |a-1|。
|a-1|。
设所求切线方程为y=kx+b,即kx-y+b=0
则圆心到直线的距离应等于圆的半径,即 =
= |a-1|恒成立。
|a-1|恒成立。
整理得2(1+k)2a2-4(1+k2)a+2(1+k2)=(k+1)2a2+2(b-2)(k+1)a+(b-2)2恒成立。
比较系数可得
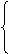 2(1+k2)=(k+1)2
2(1+k2)=(k+1)2
-4(1+k2)=2(b-2)(k+1)
2(1+k2)=(b-2)2 解之得k=1,b=0。所以,所求的切线方程是y=x。
(3)圆心坐标为(a,a-2),又设圆心坐标为(x,y),则有
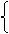 x=a
x=a
y=2-a
消去参数得x+y=2为所求的圆心的轨迹方程。
9.(2005江苏) 圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得 试建立适当的坐标系,并求动点 P的轨迹方程.
试建立适当的坐标系,并求动点 P的轨迹方程.
解:如图,以直线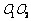 为
为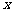 轴,线段
轴,线段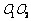 的垂直平分线为
的垂直平分线为 轴,建立平面直角坐标系,则两圆心分别为
轴,建立平面直角坐标系,则两圆心分别为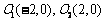 .设
.设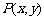 ,则
,则
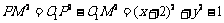 ,同理
,同理
∵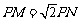 ,
,
∴ ,
,
即 ,即
,即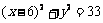 .这就是动点
.这就是动点 的轨迹方程.
的轨迹方程.
8. 已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
(1)证明:不论m取什么实数,直线l与圆恒交于两点;
(2)求直线被圆C截得的弦长最小时l的方程.
剖析:直线过定点,而该定点在圆内,此题便可解得.
(1)证明:l的方程(x+y-4)+m(2x+y-7)=0.

|
|
 2x+y-7=0, x=3,
2x+y-7=0, x=3,
x+y-4=0, y=1,
即l恒过定点A(3,1).
∵圆心C(1,2),|AC|= <5(半径),
<5(半径),
∴点A在圆C内,从而直线l恒与圆C相交于两点.
(2)解:弦长最小时,l⊥AC,由kAC=- ,
,
∴l的方程为2x-y-5=0.
7.已知圆C的圆心在直线x─y─4=0上,并且通过两圆C1:x2+y2─4x─3=0和C2:x2+y2─4y─3=0的交点,(1)求圆C的方程; (2)求两圆C1和C2相交弦的方程
解:(1)因为所求的圆过两已知圆的交点,故设此圆的方程为:x2+y2─4x─3+λ(x2+y2─4y─3)=0,
即 (1+λ)(x2+y2)─4x─4λy─3λ─3=0,
即 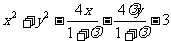 =0,
=0,
圆心为 ( ,
, ),
),
由于圆心在直线x─y─4=0上,
∴ ─
─ ─4=0, 解得 λ=─1/3
─4=0, 解得 λ=─1/3
所求圆的方程为:x2+y2─6x+2y─3=0
(2)将圆C1和圆C2的方程相减得:x+y=0,此即相交弦的方程
点评:学会利用圆系的方程解题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com