
3. ⑴由茎叶图知,分数在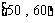 之间的频数为
之间的频数为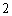 ,频率为
,频率为 ,
,
全班人数为 .
.
所以分数在 之间的频数为
之间的频数为
⑵分数在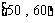 之间的总分为
之间的总分为 ;
;
分数在 之间的总分为
之间的总分为 ;
;
分数在 之间的总分数为
之间的总分数为
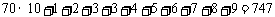 ;
;
分数在 之间的总分约为
之间的总分约为 ;
;
分数在 之间的总分数为
之间的总分数为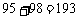 ;
;
所以,该班的平均分数为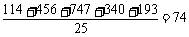 .
.
估计平均分时,以下解法也给分:
分数在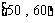 之间的频率为
之间的频率为 ;
;
分数在 之间的频率为
之间的频率为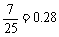 ;
;
分数在 之间的频率为
之间的频率为 ;
;
分数在 之间的频率为
之间的频率为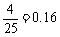 ;
;
分数在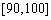 之间的频率为
之间的频率为 ;
;
所以,该班的平均分约为
频率分布直方图中 间的矩形的高为
间的矩形的高为 .
.
⑶将 之间的
之间的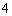 个分数编号为
个分数编号为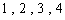 ,
, 之间的
之间的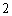 个分数编号为
个分数编号为 ,在
,在 之间的试卷中任取两份的基本事件为:
之间的试卷中任取两份的基本事件为:
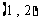 ,
, ,
,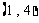 ,
, ,
,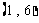
 ,
,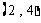 ,
,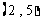 ,
,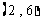 ,
,
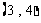 ,
,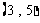 ,
,
 ,
,
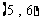 共
共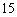 个,
个,
其中,至少有一个在 之间的基本事件有
之间的基本事件有 个,
个,
故至少有一份分数在 之间的概率是
之间的概率是 .
.
2. 解:(1)由题意得,境外游客有27人,其中9人持金卡;境内游客有9人,其中6人持银卡。设事件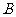 为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
事件 为“采访该团3人中,1人持金卡,0人持银卡”,
为“采访该团3人中,1人持金卡,0人持银卡”,
事件 为“采访该团3人中,1人持金卡,1人持银卡”。
为“采访该团3人中,1人持金卡,1人持银卡”。

 ………………………………………………………3分
………………………………………………………3分


所以在该团中随机采访3人,恰有1人持金卡且持银卡者少于2人的概率是 。
。
…………………………………………………………6分
(2)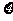 的可能取值为0,1,2,3
的可能取值为0,1,2,3
 ,
, 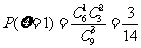
 ,
,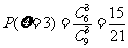 , (每个2分)
, (每个2分)
所以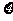 的分布列为
的分布列为
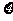 |
0 |
1 |
2 |
3 |
 |
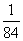 |
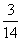 |
 |
 |
…………………………………………………………14分
所以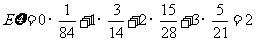 , ……………………16分
, ……………………16分
1. (1)
 P
P =
= ,
,
P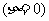 =
=
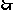

 ----------- 1分
----------- 1分
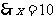 ---------- 2分
---------- 2分
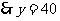
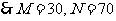 -----------3分
-----------3分
画出列联表的等高条形图 ----------4分
由列联表的等高条形图可以初步判断药物有效 -----------5分
(2)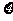 取值为0,1,2
取值为0,1,2
P =
= =
= ,
,
P =
= =
= ,
,
P =
= =
=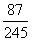 ,
,
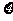 |
0 |
1 |
2 |
 |
 |
 |
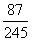 |
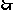
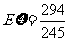 -----7分
-----7分
P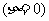 =
= =
=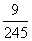
P =
=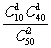 =
=
P =
= =
=
 |
0 |
1 |
2 |
 |
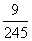 |
 |
 |
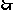
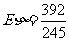 ------9分
------9分
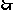
 说明药物有效
----10分
说明药物有效
----10分
(3)
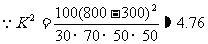 ---------11分
---------11分
由参考数据知不能够以97.5%的把握认为药物有效。 ------12分
11.(2010浙江菱湖中学二模、丹东一中2009-2010学年度下期中考试)
某单位举办2010年上海世博会知识宣传活动,进行现场抽奖,盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽” 或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行.
(1)活动开始后,一位参加者问:盒中有几张“海宝”卡?主持人答:我只知道,从盒中抽取两张都是“世博会会徽“卡的概率是 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(2)现有甲、乙、丙、丁四人依次抽奖,用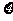 表示获奖的人数,求
表示获奖的人数,求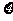 的分布列及
的分布列及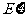 ,
, 的值.
的值.
2010年新课标省市高三数学模拟题分类
第六节 统计与概率详解答案
10.(2010东北师大附中最后一模)
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动). 某校高一·一班50名学生在上学期参加活动的次数统计如条形图所示.
(I) 求该班学生参加活动的人均次数 ;
;
(II) 从该班中任意选两名学生,求他们参加活动
次数恰好相等的概率;
 (III)从该班中任选两名学生,用
(III)从该班中任选两名学生,用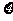 表示这两人参
表示这两人参
加活动次数之差的绝对值,求随机变量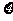 的分布列及数学期望
的分布列及数学期望 .(要求:答案用最简分数表示)
.(要求:答案用最简分数表示)
9.(2010辽宁丹东一模)
符合下列三个条件之一,某名牌大学就可录取:
①获国家高中数学联赛一等奖(保送录取,联赛一等奖从省高中数学竞赛优胜者中考试选拔);
②自主招生考试通过并且高考分数达到一本分数线(只有省高中数学竞赛优胜者才具备自主招生考试资格);
③高考分数达到该大学录取分数线(该大学录取分数线高于一本分数线).
某高中一名高二数学尖子生准备报考该大学,他计划:若获国家高中数学联赛一等奖,则保送录取;若未被保送录取,则再按条件②、条件③的顺序依次参加考试.
已知这名同学获省高中数学竞赛优胜奖的概率是0.9,通过联赛一等奖选拔考试的概率是0.5,通过自主招生考试的概率是0.8,高考分数达到一本分数线的概率是0.6,高考分数达到该大学录取分数线的概率是0.3.
(I)求这名同学参加考试次数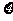 的分布列及数学期望;
的分布列及数学期望;
(II)求这名同学被该大学录取的概率.
8.(2010吉林省实验中学第八次模拟)
某市十所重点中学进行高三联考,共有5000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:
(1)根据上面的频率分布表,求①,②,③,④处的数值;
(2)根据上面的频率分布表,在所给的坐标系中画出在区间 上的频率分布直方图;
上的频率分布直方图;
(3)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从总体中任意抽取3个个体,成绩落在 中的个体数为
中的个体数为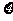 ,求
,求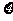 的分布列和数学期望.
的分布列和数学期望.
|
分组 |
频数 |
频率 |
 |
① |
② |
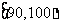 |
|
0.050 |
 |
|
0.200 |
 |
36 |
0.300 |
 |
|
0.275 |
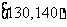 |
12 |
③ |
 |
|
0.050 |
|
合计 |
④ |
|
7.(2010陕西省高三第五次适应性训练)
某电视台综艺频道主办一种有奖过关游戏,该游戏设有两关,只有过了第一关,才能玩第二关,每关最多玩两次,连续两次失败者被淘汰出局.过关者可获奖金,只过第一关获奖金900元,两关全过获奖金3600元.某同学有幸参与了上述游戏,且该同学每一次过关的概率均为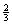 ,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
(1)求该同学仅获得900元奖金的概率;
(2)若该同学已顺利通过第一关,求他获得3600元奖金的概率;
(3)求该同学获得奖金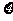 的数学期望(精确到元).
的数学期望(精确到元).
6.(2010银川二中二模)
某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
|
日 期 |
3月1日 |
3月2日 |
3月3日 |
3月4日 |
3月5日 |
温差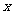 (°C) (°C) |
10 |
11 |
13 |
12 |
8 |
发芽数 (颗) (颗) |
23 |
25 |
30 |
26 |
16 |
(Ⅰ)从3月1日至3月5日中任选2天,记发芽的种子数分别为 ,求事件“m
,n均不小于25”的概率.
,求事件“m
,n均不小于25”的概率.
(Ⅱ)若选取的是3月1日与3月5日的两组数据,请根据3月2日至3月4日的数据,求出y关于x的线性回归方程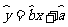 ;
;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(Ⅱ)中所得的线性回归方程是否可靠?
(参考公式:回归直线的方程是 ,其中
,其中 ,
,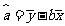 ,)
,)
5.(2010双基测试、辽宁丹东2009-2010学年度下高二期末质量监测)
一个口袋中有2个白球和 个红球(
个红球( ,且
,且 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖。
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖。
(1)试用含 的代数式表示一次摸球中奖的概率P;
的代数式表示一次摸球中奖的概率P;
(2)若 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为 ,当
,当 为何值时,
为何值时, 最大。
最大。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com