
28.(本题9分) 如图,△ABC和△ADC都是每边长相等的等边三角形,点E、F同时分别从点B、A出发,各自沿BA、AD方向运动到点A、D停止,运动的速度相同,连接EC、FC.
(1)在点E、F运动过程中∠ECF的大小是否随之变化?请说明理由;
(2)在点E、F运动过程中,以点A、E、C、F为顶点的四边形的面积变化了吗?请说明理由.
 (3)连接EF,在图中找出和
(3)连接EF,在图中找出和 ∠ACE相等的所有角,并说明理由.
∠ACE相等的所有角,并说明理由.
(4)若点E、F在射线BA、射线AD上继续运动下去,(1)小题中的结论还成立吗?(直接写出结论,不必说明理由)
高新区2009-2010学年度第二学期期末调研测试
27.(本题7分) 七(1)班学生参加学校组织的“迎世博”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表.
(1)频数分布表中a= ▲ ,b= ▲ ;
(2)学校设定成绩在79.5分及以上的学生将获得一等奖或二等奖,一等奖奖励作业本10本及世博会吉祥物 海宝3个,二等奖奖励作业本6本及海宝1个.已知七(1)班学生共获得作业本158本,请求出七(1)班学生共获得海宝多少个?
海宝3个,二等奖奖励作业本6本及海宝1个.已知七(1)班学生共获得作业本158本,请求出七(1)班学生共获得海宝多少个?
七 (1)班“迎世博”知识竞赛成绩频数分布表
(1)班“迎世博”知识竞赛成绩频数分布表
|
分数段 |
49.5-59.5 |
59.5-69.5 |
69.5-79.5 |
79.5-89.5 |
 89.5-99.5 89.5-99.5 |
|
频
数 |
a |
9 |
10 |
14 |
5 |
|
频
率 |
0.05 |
b |
0.250 |
0.350 |
0.125 |
26.(本题6分) 如图①,直线l过正方形ABCD的顶点B,A、C两顶点在直线l同侧,过点A、C分别作AE⊥直线l、CF⊥直线l.
(1)试说明:EF=AE+CF;
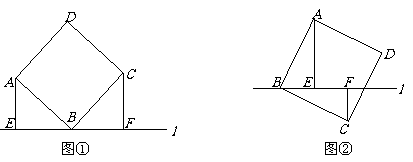 (2)如图②,当A、C两顶点在直线
(2)如图②,当A、C两顶点在直线 两侧时,其它条件不变,猜想EF、AE、CF满足什么数量关系(直接写出答案,不必说明理由).
两侧时,其它条件不变,猜想EF、AE、CF满足什么数量关系(直接写出答案,不必说明理由).
25. (本题6分)
某学校为了进一步丰富学生的体育活动,欲增购一些体育器材,为此对该校一部分学生进行了一次“你最喜欢的体育活动”的问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
(本题6分)
某学校为了进一步丰富学生的体育活动,欲增购一些体育器材,为此对该校一部分学生进行了一次“你最喜欢的体育活动”的问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
请根据图中提供的信息,完成下列问题:
(1)在这次问卷调查中,一共抽查了 ▲ 名学生;
(2)请将图②补充完整;
(3)图①中,“其它”部分所对应的圆心角为 ▲ °;
(4)若在所有问卷调查中任意抽一张,则抽到“最喜欢的体育活动”是“踢毽”的概率是 ▲ ;
(5)如果全校有1960名学生,则全校学生中,最喜欢“跳绳”活动的学生约有多少人?
24.(本题6分) 已知x+2y=5,xy=1.求下列各式的值:
(1) (2)
(2)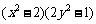
23.(本题6分) 如图,四边形ABCD中,CD∥AB,E是AD中点,
CE交BA延长线于点F.
(1)试说明:CD=AF;
(2)若BC=BF,试说明:BE⊥CF.
22.(本题5分) 已知关于x、y的二元一次方程组 的解互为相反数,求x、y、a的值.
的解互为相反数,求x、y、a的值.

21.(本题4分)
解方程组 
20.因式分解 (每小题3分,共6分)
(1)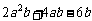 (2)
(2)
19.计算 (每小题3分,共9分)
(1) (2)
(2)
(3) ,其中
,其中
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com