
(一)解答题:
1、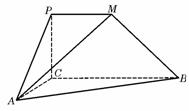 (07四川)如图,
(07四川)如图,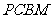 是直角梯形,∠
是直角梯形,∠ =90°,
=90°,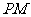 ∥
∥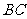 ,
,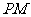 =1,
=1,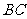 =2,又
=2,又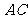 =1,∠
=1,∠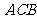 =120°,
=120°,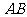 ⊥
⊥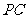 ,直线
,直线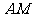 与直线
与直线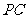 所成的角为60°。
所成的角为60°。
(Ⅰ)求证:平面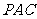 ⊥平面
⊥平面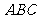 ;
;
(Ⅱ)求二面角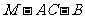 的大小;
的大小;
(Ⅲ)求三棱锥 的体积。
的体积。
2、(07福建)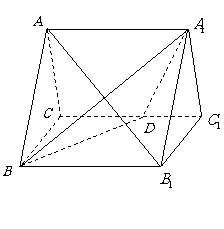 如图,正三棱柱
如图,正三棱柱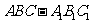 的所有棱长都为
的所有棱长都为
 ,
,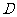 为
为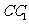 中点.
中点.
(Ⅰ)求证: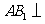 平面
平面 ;
;
(Ⅱ)求二面角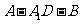 的大小;
的大小;
(Ⅲ)求点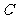 到平面
到平面 的距离.
的距离.
3、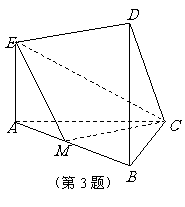 (07浙江)在如图所示的几何体中,
(07浙江)在如图所示的几何体中, 平面
平面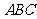 ,
,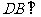 平面
平面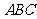 ,
, ,且
,且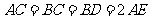 ,
,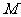 是
是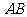 的中点.
的中点.
(I)求证: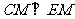 ;
;
(II)求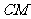 与平面
与平面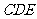 所成的角.
所成的角.
4、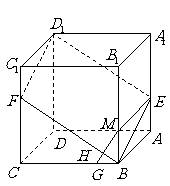 (07江苏)如图,已知
(07江苏)如图,已知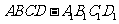 是棱长为
是棱长为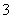 的正方体,
的正方体,
点 在
在 上,点
上,点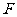 在
在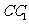 上,且
上,且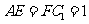 .
.
(1)求证: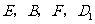 四点共面;
四点共面;
(2)若点 在
在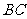 上,
上,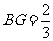 ,点
,点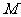 在
在 上,
上,
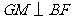 ,垂足为
,垂足为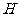 ,求证:
,求证: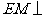 平面
平面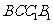 ;
;
5、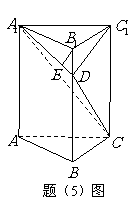 (07重庆)如题(5)图,在直三棱柱
(07重庆)如题(5)图,在直三棱柱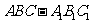 中,
中,
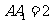 ,
,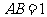 ,
,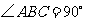 ;
;
点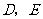 分别在
分别在 ,
,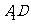 上,且
上,且 ,
,
四棱锥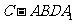 与直三棱柱的体积之比为
与直三棱柱的体积之比为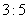 .
.
(Ⅰ)求异面直线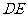 与
与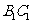 的距离;
的距离;
(Ⅱ)若 ,求二面角
,求二面角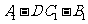 的平面角的正切值.
的平面角的正切值.
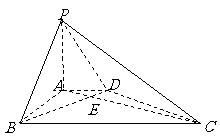
6、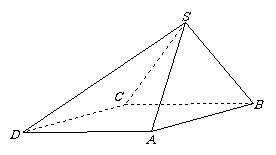 (07全国Ⅰ)四棱锥
(07全国Ⅰ)四棱锥 中,底面
中,底面 为平行四边形,侧面
为平行四边形,侧面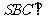 底面
底面 .已知
.已知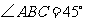 ,
,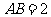 ,
,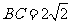 ,
,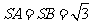 .
.
(Ⅰ)证明 ;
;
(Ⅱ)求直线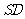 与平面
与平面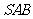 所成角的大小.
所成角的大小.
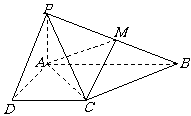
 例1、(07陕西) 如图,在底面为直角梯形的四棱锥
例1、(07陕西) 如图,在底面为直角梯形的四棱锥 中,
中,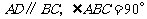 ,
,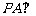 平面
平面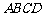 .
.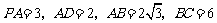 .
.
(Ⅰ)求证: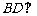 平面
平面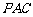 ;
;
(Ⅱ)求二面角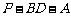 的大小.
的大小.
 例2、(05全国Ⅰ) 已知四棱锥
例2、(05全国Ⅰ) 已知四棱锥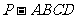 的底面为直角梯形,
的底面为直角梯形,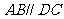 ,
,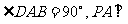 底面
底面 ,且
,且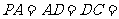
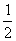
 1,
1,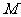 是
是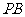 的中点。
的中点。
(Ⅰ)证明:面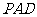 ⊥面
⊥面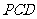 ;
;
(Ⅱ)求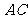 与
与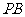 所成的角;
所成的角;
(Ⅲ)求面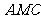 与面
与面 所成二面角的大小。
所成二面角的大小。
(三)解答题:
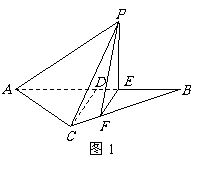
7、(06江苏)在正三角形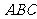 中,
中,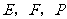 分别是
分别是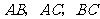 边上的点,满足
边上的点,满足
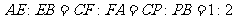 (如图1)。将△
(如图1)。将△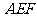 沿
沿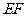 折起到
折起到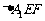 的位置,
的位置,
使二面角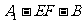 成直二面角,连结
成直二面角,连结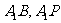 (如图2)。(Ⅰ)求证:
(如图2)。(Ⅰ)求证: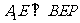 平面;(Ⅱ)求直线
平面;(Ⅱ)求直线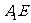 与平面
与平面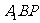 所成角的大小;(Ⅲ)求二面角
所成角的大小;(Ⅲ)求二面角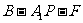 的大小(用反三角函数表示)
的大小(用反三角函数表示)

(二)填空题:
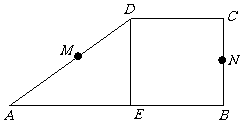
2、(05浙江)设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________;

3、 (06全国Ⅰ)已知正四棱锥的体积为12,底面对角线的长为
(06全国Ⅰ)已知正四棱锥的体积为12,底面对角线的长为 ,则侧面与底面所成的二面角等于_______________;
,则侧面与底面所成的二面角等于_______________;
4、(06山东)如图,已知正三棱柱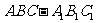 的所有棱长都相等,
的所有棱长都相等,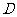 是
是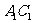 的中点,则直线
的中点,则直线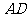 与平面
与平面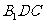 所成角的正弦值为
;
所成角的正弦值为
;
5、(06四川)在三棱锥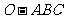 中,三条棱
中,三条棱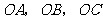 两两互相垂直,且
两两互相垂直,且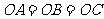 ,
,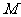 是
是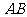 的中点,则
的中点,则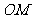 与平面
与平面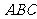 所成角的大小是______________(用反三角函数表示);
所成角的大小是______________(用反三角函数表示);
6、(06辽宁16)若一条直线与一个正四棱柱各个面所成的角都为 ,则
,则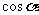 =______。
=______。
(一)选择题:
1、(06四川)已知二面角 的大小为
的大小为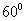 ,
,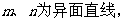

 ( )
( )
(A)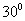 (B)
(B)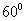 (C)
(C)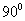 (D)
(D)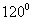
 例1、(07广东)如图1所示,等腰
例1、(07广东)如图1所示,等腰 的底边
的底边 ,高
,高 ,点
,点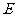 是线段
是线段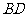 上异于点
上异于点 的动点,点
的动点,点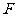 在
在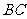 边上,且
边上,且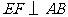 ,现沿
,现沿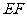 将
将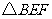 折起到
折起到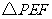 的位置,使
的位置,使 ,记
,记 ,
, 表示四棱锥
表示四棱锥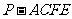 的体积.
的体积.
(1)求 的表达式;
的表达式;
(2)当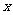 为何值时,
为何值时, 取得最大值?
取得最大值?
(3)当 取得最大值时,求异面直线
取得最大值时,求异面直线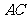 与
与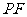 所成角的余弦值。
所成角的余弦值。
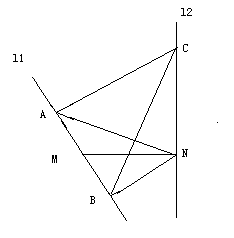 例2、(06全国Ⅰ)如图,
例2、(06全国Ⅰ)如图,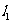 、
、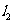 是互相垂直的异面直线,
是互相垂直的异面直线,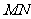 是它们的公垂线段。点
是它们的公垂线段。点 在
在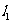 上,
上,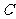 在
在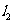 上,
上,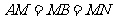 。(Ⅰ)证明
。(Ⅰ)证明 ⊥
⊥ ;(Ⅱ)若
;(Ⅱ)若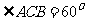 ,求
,求 与平面
与平面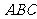 所成角的余弦值。
所成角的余弦值。
5.二分法求函数的零点的近似值适合于怎样的零点?
[例题解析]
例1:求 近似值(精确到0.01)
近似值(精确到0.01)
例2:求方程 的无理根(精确到0.01)
的无理根(精确到0.01)
4.用二分法求函数零点的一般步骤是什么?
3.求函数变号零点的近似值的一种计算方法是 ,其定义是:已知函数 定义在区间D上,求它在D上的一个变号零点
定义在区间D上,求它在D上的一个变号零点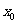 的近似值
的近似值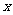 ,使它与零点的误差 ,即使得 。
,使它与零点的误差 ,即使得 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com