

3.下列各句中,加点的熟语使用恰当的一项是( )
A 如今,留守在家的外出务工人员子女得到了老师、学校和社会各界无所不至的关爱,使他们能够健康快乐的成长。
B 在十运会上,雅典奥运10000米冠军邢慧娜因挤压对手而被取消了冠军资格。人们不禁要问:这种偷鸡不成蚀把米的行径在十运会上频频出现的真正原因到底是什么。
C 尽管伊拉克新宪法在全民公决中通过,但摆在伊美当局面前首当其冲的问题仍然是如何平息种族仇视和恐怖袭击。
D 每天凌晨,人民公园里就挤满了那些初生牛犊不怕虎的晨练老人。
2.依次填入下列各横线上的词语,最恰当的一组是( )
① 南亚大地震爆发后,包括中国在内的国际社会纷纷解囊相助,以帮助巴基斯坦灾民 难关。
② 10月15日22时08分,“神舟”六号飞船已在太空绕地球飞行了56圈。
③ 面对穷凶极恶的歹徒,普通公民
能挺身而出, 被劫持的人质是这位警察的妻子呢?(A 何况 B况且 C尚且)
A度过 截至 况且/何况
B渡过 截止 尚且/况且
C渡过 截至 尚且/何况
D度过 截止 况且/况且
1.下列词语中加点汉字的读音,全都不相同的一组是( )
A 伉俪 高亢 沆瀣一气 引吭高歌
B 酝酿 踉跄 朗朗乾坤 锒铛入狱
C 靓妆 倩影 绥靖政策 风平浪静
D 泡影 咆哮 越俎代庖 炮羊肉串
9.(2003上海)如下图,某隧道设计为双向四车道,车道总宽22 m,要求通行车辆限高4.5 m,隧道全长2.5 km,隧道的拱线近似地看成半个椭圆形状.
(1)若最大拱高h为6 m,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6 m,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
(半个椭圆的面积公式为S= lh,柱体体积为底面积乘以高.本题结果均精确到0.1 m)
lh,柱体体积为底面积乘以高.本题结果均精确到0.1 m)
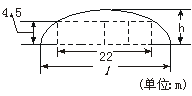 (1)解:如下图建立直角坐标系,则点P(11,4.5),
(1)解:如下图建立直角坐标系,则点P(11,4.5),
椭圆方程为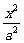 +
+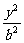 =1.将b=h=6与点P坐标代入椭圆方程,得a=
=1.将b=h=6与点P坐标代入椭圆方程,得a=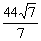 ,此时l=2a=
,此时l=2a=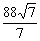 ≈33.3.因此隧道的拱宽约为33.3 m.
≈33.3.因此隧道的拱宽约为33.3 m.
(2)解法一:由椭圆方程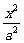 +
+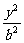 =1,得
=1,得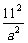 +
+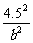 =1.
=1.
因为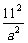 +
+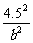 ≥
≥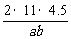 ,即ab≥99,且l=2a,h=b,所以S=
,即ab≥99,且l=2a,h=b,所以S=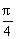 lh=
lh=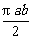 ≥
≥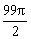 .
.
当S取最小值时,有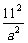 =
=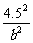 =
=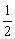 ,
,
得a=11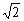 ,b=
,b=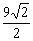 .
.
此时l=2a=22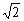 ≈31.1,h=b≈6.4.
≈31.1,h=b≈6.4.
故当拱高约为6.4 m、拱宽约为31.1 m时,土方工程量最小.
解法二:由椭圆方程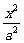 +
+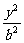 =1,
=1,
得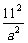 +
+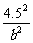 =1.
=1.
于是b2=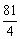 ·
·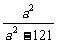 .
.
a2b2=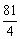 (a2-121+
(a2-121+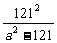 +242)≥
+242)≥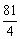 (2
(2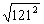 +242)=81×121,
+242)=81×121,
即ab≥99,当S取最小值时,
有a2-121=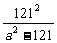 .
.
得a=11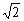 ,b=
,b=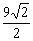 ,以下同解法一.
,以下同解法一.
10 (2006四川)已知两定点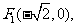
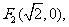 满足条件
满足条件 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点 如果
如果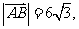 且曲线E上存在点C,使
且曲线E上存在点C,使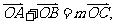 求
求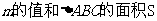
解:由双曲线的定义可知,曲线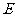 是以
是以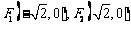 为焦点的双曲线的左支,
为焦点的双曲线的左支,
且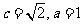 ,易知
,易知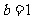
 故曲线
故曲线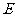 的方程为
的方程为
设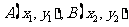 ,由题意建立方程组
,由题意建立方程组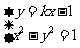
消去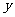 ,得
,得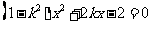
又已知直线与双曲线左支交于两点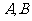 ,有
,有
 解得
解得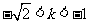
又∵ 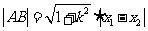
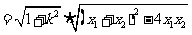
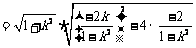
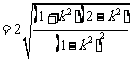
依题意得 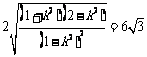 整理后得
整理后得 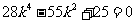
∴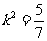 或
或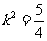 但
但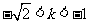 ∴
∴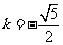
故直线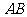 的方程为
的方程为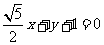
设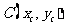 ,由已知
,由已知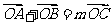 ,得
,得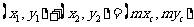
∴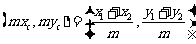 ,
,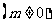
又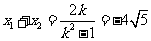 ,
,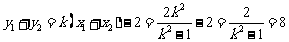
∴点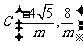
将点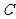 的坐标代入曲线
的坐标代入曲线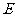 的方程,得
的方程,得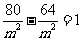
得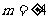 ,但当
,但当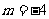 时,所得的点在双曲线的右支上,不合题意
时,所得的点在双曲线的右支上,不合题意
∴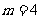 ,
,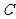 点的坐标为
点的坐标为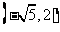
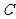 到
到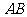 的距离为
的距离为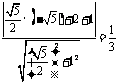
∴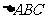 的面积
的面积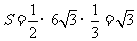
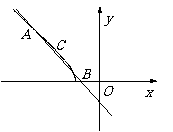
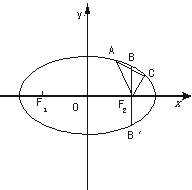
[探索题](2002春全国)已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2,并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10.椭圆上不同的两点A(x1,y1)、C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列.
(1)求该椭圆的方程;
(2)求弦AC中点的横坐标;
(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围.
(1)解:由椭圆定义及条件知
2a=|F1B|+|F2B|=10,得a=5.又c=4,
所以b=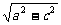 =3.
=3.
故椭圆方程为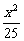 +
+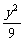 =1.
=1.
(2)解:由点B(4,yB)在椭圆上,得|F2B|=|yB|=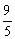 .
.
方法一:因为椭圆右准线方程为x=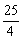 ,离心率为
,离心率为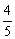 .
.
根据椭圆定义,有|F2A|=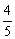 (
(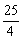 -x1),|F2C|=
-x1),|F2C|=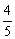 (
(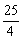 -x2).
-x2).
由|F2A|、|F2B|、|F2C|成等差数列,得
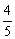 (
(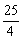 -x1)+
-x1)+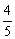 (
(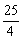 -x2)=2×
-x2)=2×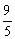 .
.
由此得出x1+x2=8.
设弦AC的中点为P(x0,y0),
则x0=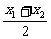 =
=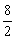 =4.
=4.
方法二:由|F2A|、|F2B|、|F2C|成等差数列,得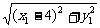 +
+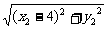 =2×
=2×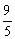 , ①
, ①
由A(x1,y1)在椭圆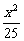 +
+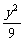 =1上,得
=1上,得
y12=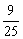 (25-x12),
(25-x12),
所以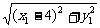
=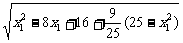
=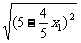 =
=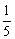 (25-4x1) ②
(25-4x1) ②
同理可得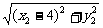 =
=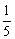 (25-4x2) ③
(25-4x2) ③
将②③代入①式,得
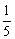 (25-4x1)+
(25-4x1)+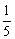 (25-4x2)=
(25-4x2)=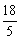 .
.
所以x1+x2=8.
设弦AC的中点为P(x0,y0),
则x0=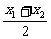 =
=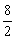 =4.
=4.
(3)解法一:由A(x1,y1),C(x2,y2)在椭圆上,得
9x12+25y12=9×25, ④
9x22+25y22=9×25. ⑤
由④-⑤得9(x12-x22)+25(y12-y22)=0,
即9(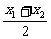 )+25(
)+25(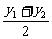 )(
)(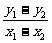 )=0(x1≠x2).
)=0(x1≠x2).
将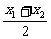 =x0=4,
=x0=4,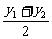 =y0,
=y0,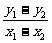 =-
=-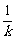 (k≠0)代入上式,得
(k≠0)代入上式,得
9×4+25y0(-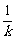 )=0(k≠0).
)=0(k≠0).
由上式得k=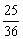 y0(当k=0时也成立).
y0(当k=0时也成立).
由点P(4,y0)在弦AC的垂直平分线上,得
y0=4k+m,
所以m=y0-4k=y0-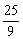 y0=-
y0=-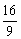 y0.
y0.
由P(4,y0)在线段BB′(B′与B关于x轴对称)的内部,得-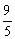 <y0<
<y0<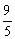 .
.
所以-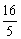 <m<
<m<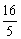 .
.
评述:在推导过程中,未写明“x1≠x2”“k≠0”“k=0时也成立”及把结论写为“-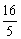 ≤m≤
≤m≤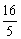 ”也可以.
”也可以.
解法二:因为弦AC的中点为P(4,y0),
所以直线AC的方程为
y-y0=-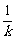 (x-4)(k≠0). ⑥
(x-4)(k≠0). ⑥
将⑥代入椭圆方程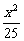 +
+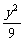 =1,得
=1,得
(9k2+25)x2-50(ky0+4)x+25(ky0+4)2-25×9k2=0.
所以x1+x2=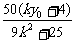 =8.
=8.
解得k=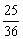 y0(当k=0时也成立).
y0(当k=0时也成立).
以下步骤同解法一.
8.(2005上海文)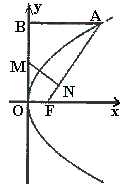 已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4、且位于
已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4、且位于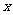 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于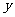 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
(1)求抛物线方程;
(2)过M作MN⊥FA,垂足为N,求点N的坐标;
(3)以M为圆心,MB为半径作圆M,当K(m.0)是x轴上一动点时,讨论直线AK与圆M的位置关系.
解:(1)抛物线y2=2px的准线为
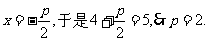
∴抛物线方程为y2= 4x.
(2)∵点A的坐标是(4,4), 由题意得B(0,4),M(0,2),
又∵F(1,0), ∴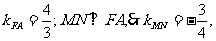
则FA的方程为y=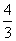 (x-1),MN的方程为
(x-1),MN的方程为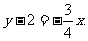
解方程组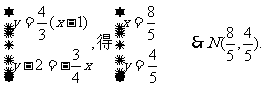
(3)由题意得,圆M的圆心是点(0,2),半径为2.
当m=4时,直线AK的方程为x=4,此时,直线AK与圆M相离,
当m≠4时,直线AK的方程为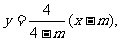 即为
即为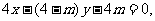
圆心M(0,2)到直线AK的距离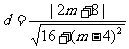 ,令
,令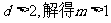
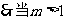 时,直线AK与圆M相离;
时,直线AK与圆M相离;
当m=1时,直线AK与圆M相切;
当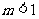 时,直线AK与圆M相交.
时,直线AK与圆M相交.
7.已知椭圆的焦点是F1(-1,0),F2(1,0),P为椭圆上的一点,且|F1F2|是|PF1|和|PF2|的等差中项。(1)求椭圆方程; (2)若点P在第三象限,且∠P F1F2=1200,求tan∠F1PF2。
解:(1)由题设2|F1F2|=|PF1|+|PF2|,c=1。∴2a=4,∴b=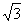 。∴椭圆方程为
。∴椭圆方程为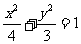 。
。
(2)设∠F1PF2=θ,则∠PF2 F1=600-θ,由正弦定理并结合等比定理可得到
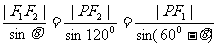
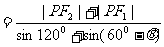 ,
,
∴化简可得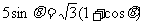 ,∴
,∴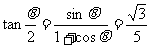 ,
,
从而可求得tan∠F1PF2=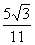 。
。
思维点拨:解与△P F1F2有关的问题(P为椭圆上的点)常用正弦定理或余弦定理,并且结合|PF1|+|PF2|=2a来求解。
6.(2005江西)以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,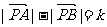 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②设定圆C上一定点A作圆的动点弦AB,O为坐标原点,若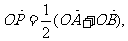 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程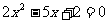 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
简答提示:1-4.DAAD; 5.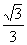 ; 6.③④.
; 6.③④.
[解答题]
5.(2005江苏卷)点P(-3,1)在椭圆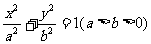 的左准线上,过点P且方向为
的左准线上,过点P且方向为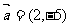 的光线,经直线
的光线,经直线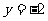 反射后通过椭圆的左焦点,则这个椭圆的离心率为_______
反射后通过椭圆的左焦点,则这个椭圆的离心率为_______
4.(2006湖北)设过点P(x,y)的直线分别与x轴的正半轴和y轴的正半轴交于A,B两点,点Q与点P关于y轴对称,O为坐标原点,若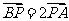 ,且
,且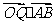 =1,则P点的轨迹方程是( )
=1,则P点的轨迹方程是( )
A. 3x2+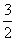 y2=1 (x>0,y>0)
B.3x2-
y2=1 (x>0,y>0)
B.3x2-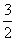 y2=1(x>0, y>0)
y2=1(x>0, y>0)
C.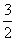 x2-3y2=1(x>0,y>0)
D.
x2-3y2=1(x>0,y>0)
D. 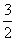 x2+3y2=1(x>0,y>0)
x2+3y2=1(x>0,y>0)
[填空题]
3.(2006辽宁)曲线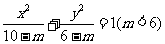 与曲线
与曲线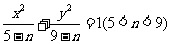 的 ( )
的 ( )
A.焦距相等 B.离心率相等
C.焦点相同 D.准线相同
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com