

20.(本小题满分13分)
已知数列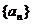 满足
满足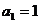 ,点
,点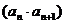 在直线
在直线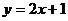 上,数列
上,数列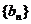 满足
满足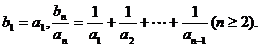
(1)求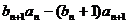 的值;
的值;
(2)求证:
19.(本小题满分13分)
张家界某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值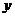 万元与投入
万元与投入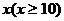 万元之间满足:
万元之间满足: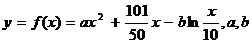 为常数。当
为常数。当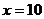 万元时,
万元时,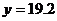 万元;当
万元;当 万元时,
万元时, 万元。(参考数据:
万元。(参考数据: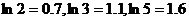 )
)
(1)求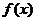 的解析式;
的解析式;
(2)求该景点改造升级后旅游利润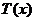 的最大值。(利润=旅游增加值-投入)
的最大值。(利润=旅游增加值-投入)
18.(本小题满分12分)
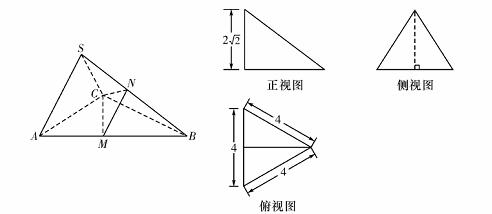 下图分别为三棱锥S-ABC的直观图与三视图,在直观图中,
下图分别为三棱锥S-ABC的直观图与三视图,在直观图中,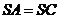 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
(1)求证: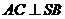 ;
;
(2)求二面角M-NC-B的余弦值。
17.(本小题满分12分)
“上海世博会”于2010年5月1日至10月31日在上海举行,世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所,陈列其中的艺术品是体现兼容并蓄,海纳百川的重要文化载体,为此,上海世博会事物协调局举办“中国2010年上海世博会”中国馆·贵宾厅艺术品方案征集活动,某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应证,假设代表中有中国画、书法、油画入选“中国馆·贵宾厅”的概率均为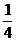 ,陶艺入选“中国馆·贵宾厅”的概率为
,陶艺入选“中国馆·贵宾厅”的概率为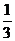 。
。
(1)求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率;
(2)设该地美术馆选送的四件代表作中入选“中国馆·贵宾厅”的作品件数为随机变量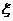 ,求
,求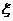 的数学期望。
的数学期望。
16.(本小题满分12分)
已知向量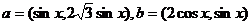 ,定义
,定义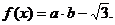
(1)求函数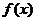 的单调递减区间;
的单调递减区间;
(2)若函数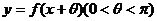 为偶函数,求
为偶函数,求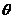 的值。
的值。
15.设代数方程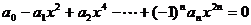 有
有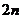 个不同的根
个不同的根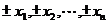 ,则
,则
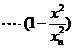 ,比较两边
,比较两边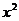 的系数得
的系数得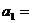 (用
(用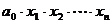 表示);若已知展开式
表示);若已知展开式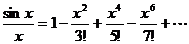 对
对 成立,则由于
成立,则由于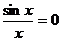 有无穷多个根:
有无穷多个根: 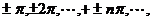 于是
于是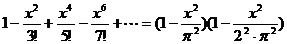
 ,利用上述结论可得
,利用上述结论可得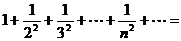 。
。
14.已知M是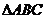 内的一点(不含边界),且
内的一点(不含边界),且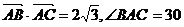 °,若
°,若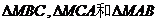 的面积分别为
的面积分别为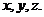
(1)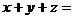 ;
;
(2)定义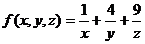 ,则
,则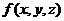 的最小值是
。
的最小值是
。
13.设双曲线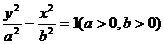 的渐近线与抛物线
的渐近线与抛物线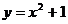 相切,则该双曲线的离心率等于 。
相切,则该双曲线的离心率等于 。
12.若曲线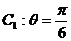
 与曲线
与曲线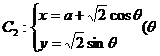 为参数,
为参数,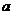 为常数,
为常数, )有两个交点A、B,且|AB|=2,则实数
)有两个交点A、B,且|AB|=2,则实数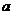 的值为 。
的值为 。
11.正三棱柱的底面边长为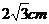 ,高为
,高为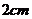 ,则它
,则它
的外接球的表面积为 cm2.(结果保留 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com